Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Краткая теория. Устройство, служащее для накопления большого количества энергии в виде электрического поля, называется конденсатором

Устройство, служащее для накопления большого количества энергии в виде электрического поля, называется конденсатором. Всякий конденсатор состоит из двух и более металлических обкладок, отделенных одна от другой слоем диэлектрика. Если сообщить конденсатору заряд q, то разность потенциалов (напряжение между обкладками) примет значение U, определяемое из соотношения:

, (14.1)

где С – коэффициент пропорциональности, получивший название электроемкости.

Единица емкости в системе СИ называется фарад (Ф). Один фарад - это емкость такого конденсатора, который одним кулоном электричества заряжается до разности потенциалов в один вольт. Это очень большая емкость. Поэтому на практике часто применяются доли этой единицы: микрофарад (мкФ) – 10^-6 фарада и пикофарад (пф) – 10^-12 фарада.

От величины заряда емкость конденсатора не зависит. Она определяется геометрическими характеристиками и диэлектрической проницаемостью e заполняющего его диэлектрика. Например, для плоского конденсатора:

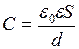, (14.2)

где S – площадь обкладки конденсатора,

d – расстояние между обкладками,

e₀ – электрическая постоянная.

Емкость цилиндрического конденсатора определяется формулой:

, (14.3)

где l – длина конденсатора,

r ₁, r₂ – радиусы внутренней и внешней обкладок соответственно.

Помимо емкости каждый конденсатор характеризуется предельным значением напряжения U_max, которое можно прикладывать к обкладкам конденсатора, не опасаясь его пробоя.

Энергия электрического поля конденсатора определяется формулами:

. (14.4)

Конденсаторы часто соединяют в батареи. При параллельном соединении конденсаторов их общая емкость равна сумме емкостей отдельных конденсаторов. Если параллельно соединены n конденсаторов, то общая емкость батареи определяется формулой:

. (14.5)

При последовательном соединении величина, обратная емкости батареи, равна сумме величин, обратных емкостям отдельных конденсаторов. В общем случае для n конденсаторов справедливо равенство:

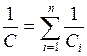. (14.6)

Конденсатор, включенный в цепь постоянного тока, представляет собой разрыв в цепи, и ток по такой цепи протекать не будет. При включении конденсатора в цепь переменного тока последний не будет представлять собой разрыва в цепи, так как в диэлектрике конденсатора цепь замыкается токами смещения. (В сущности, здесь происходит периодическая зарядка и разрядка конденсатора под действием переменного напряжения.)

Пусть к конденсатору С приложено переменное синусоидальное напряжение U:

, (14.7)

где U ₀ – амплитуда напряжения,

– круговая частота,

t – текущее значение времени.

Подставляя значение напряжения (14.7) в формулу (14.1), получим функцию изменения заряда на конденсаторе:

. (14.8)

Периодическая перезарядка конденсатора вызовет протекание через него периодического тока:

. (14.9)

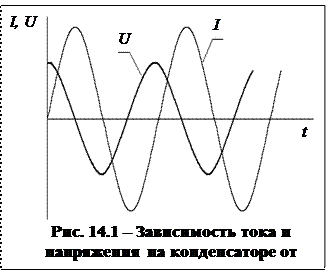Если сравнить между собой выражение для напряжения (14.7) и выражение для тока (14.9), то видно, что ток через конденсатор по фазе опережает напряжение на p/2, что соответствует четверти периода.

Таким образом, если синусоидальное напряжение прикладывается к емкости, то ток максимален в тот момент, когда напряжение начинает расти от нуля. Когда напряжение на конденсаторе максимальное, то ток равен нулю (рис. 14.1).

Амплитудное значение силы тока I ₀ может быть записано согласно уравнению (14.9) в виде:

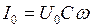(14.10)

или, по аналогии с законом Ома, в виде:

. (14.11)

В этом выражении величина называется реактивным или емкостным сопротивлением конденсатора. Таким образом, амплитуда переменного тока, протекающего через конденсатор, зависит как от величины емкости, так и от частоты.

Обычно для практических целей удобно пользоваться не амплитудными, а эффективными значениями силы тока и напряжения, которые определяются выражениями:

, . (14.12)

Для синусоидальных токов:

, . (14.13)

Эффективное значение силы переменного тока равно силе постоянного тока, выделяющего на активном сопротивлении в цепи такое же количество теплоты, что и переменный ток. Амперметры и вольтметры для переменного тока градуируют таким образом, что они показывают эффективные значения силы тока и напряжения.

Если емкость С взять в фарадах, а w= 2 p·f, (f – частота тока в герцах), то выражая в формуле (14.10) I ₀ и U ₀ через эффективные значения, получим:

. (14.14)

Решая это уравнение относительно С, будем иметь:

. (14.15)

Из этого уравнения следует, что частота переменного тока может быть записана в виде:

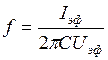(14.16)