
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Классы точности электроизмерительных приборов. Погрешность электрических измерений и способы ее минимизации при выборе измерительного прибора.
|
|
ОТВЕТ:
1) Абсолютная погрешность  - это разность между измеренным значением электрической величины (ЭВ) AИ и её действительным значением
- это разность между измеренным значением электрической величины (ЭВ) AИ и её действительным значением  .
. 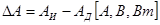 . Действительное значение измерения электрической величины (тока напряжения, мощности) всегда неизвестно, поэтому его можно определить только по прибору:
. Действительное значение измерения электрической величины (тока напряжения, мощности) всегда неизвестно, поэтому его можно определить только по прибору:
1.1. В случае единичного измерения – по показаниям эталонного прибора АЭ (образцового или более очного, чем измеряющий, например, класса 0, 02-0, 05-0, 1), включённого одновременно с рабочим измерительным прибором, то есть принимаем, что  .
.
1.2. В случае нескольких измерений – как среднее арифметическое значение из результатов этих измерений.  .
.
1.3. В случае единичного измерения и при отсутствии эталонного электроизмерительного прибора, возможную наибольшую абсолютную погрешность можно вычислить по классу точности (Кл), указанному на шкале рабочего измерительного прибора: 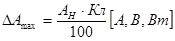 .
.
2. Относительная погрешность δ – это выраженное в процентах отношение абсолютной погрешности к действительному значению измеряемой электрической величины.  . Поскольку при правильном выполнении условий проведения измерений на электроизмерительном приборе высокого класса точности, разница между измеренным и действительным значениями электрических величин достаточно мала, то практически, в большинстве случаев, принимают:
. Поскольку при правильном выполнении условий проведения измерений на электроизмерительном приборе высокого класса точности, разница между измеренным и действительным значениями электрических величин достаточно мала, то практически, в большинстве случаев, принимают:  . Поэтому возможную наибольшую абсолютную погрешность можно вычислить по классу точности рабочего измерительного прибора:
. Поэтому возможную наибольшую абсолютную погрешность можно вычислить по классу точности рабочего измерительного прибора: 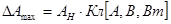 , а для определения относительной погрешности используют формулу
, а для определения относительной погрешности используют формулу 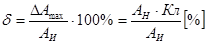 .
.
3) Приведённая погрешность γ – это отношение относительной погрешности к номинальному значению (предельное измерение) измерительного прибора, выраженная в процентах:  .
.
4) Класс точности измерительного прибора (Кл) – это нормированное (стандартное) значение возможной наибольшей приведённой погрешности электроизмерительного прибора. 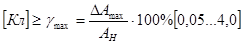 . Классы точности электроизмерительного прибора стандартизированы следующими значениями: 0, 02-0, 05-0, 1-0, 2-0, 5-1-1, 5-2, 5-4, так что по известному классу можно легко вычислить возможную наибольшую абсолютную погрешность выполненного единичного измерения.
. Классы точности электроизмерительного прибора стандартизированы следующими значениями: 0, 02-0, 05-0, 1-0, 2-0, 5-1-1, 5-2, 5-4, так что по известному классу можно легко вычислить возможную наибольшую абсолютную погрешность выполненного единичного измерения. 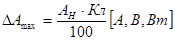 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Переменный электрический ток. Способы представления синусоидальных величин. Основные характеристики переменного тока. Период, частота, начальная фаза, сдвиг фаз, действующее значение переменного тока.
ОТВЕТ: Переменным электрическим током – называется электрический ток, величина и направление которого изменяется по синусоидальному закону. 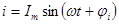 .
.
Способы представления синусоидальной величины:
1) Алгебраический 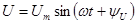 .
.
2) Графический (волновая диаграмма): 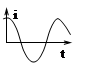 .
.
3) Векторный (с помощью векторных диаграмм):  .
.
4) С помощью комплексных чисел (символический метод):  .
.
Основные характеристики переменного тока:
 , где
, где  - мгновенное значение силы тока,
- мгновенное значение силы тока,  - амплитудное значение силы тока,
- амплитудное значение силы тока,  - фаза,
- фаза,  - циклическая частота,
- циклическая частота,  - начальная фаза.
- начальная фаза.
1) Амплитудное значение (Im, Um, Em) – наибольшее значение функции за период.
2) Период – длительность полного цикла изменения синусоидальной величины.  .
.
3) Циклическая частота ( ) – число полных циклов изменения синусоидальной величины в единицу времени.
) – число полных циклов изменения синусоидальной величины в единицу времени.  .
.
4) Угловая частота – скорость изменения аргумента функции  .
.
5) Линейное значение – значение функции в заданный момент времени. 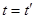 .
.  .
.
6) Начальная фаза ( ) – значение аргумента функции в нулевой момент времени.
) – значение аргумента функции в нулевой момент времени.  .
.  .
.
Если начальная фаза  отсчитывается от начала функции к началу координат по направлению оси абсцисс, то начальная фаза положительна. Начальная фаза зависит от выбора момента времени.
отсчитывается от начала функции к началу координат по направлению оси абсцисс, то начальная фаза положительна. Начальная фаза зависит от выбора момента времени.  .
.
7) Сдвиг фаз – разность начальных фаз напряжения и тока. Сдвиг фаз электрической цепи не зависит от выбора момента времени, а определяется характером электрической цепи. Если ток опережает напряжение, то характер цепи – емкостной. Если напряжение опережает ток, то характер цепи – индуктивный.
Резистивный 
| φ R=0 |
Индуктивный 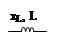
| φ L= + 90 |
Ёмкостной 
| φ C= - 90 |
Метод векторных диаграмм. Основные характеристики переменною тока. Применение комплексного метода для анализа электрических цепей переменного тока (алгебраическая, тригонометрическая и показательная форма).
ОТВЕТ: Любая электрическая синусоидальная величина на плоскости может быть представлена вращающимся против часовой стрелки радиус-вектором, модуль которого равен амплитуде функции, а скорость вращения – угловой частоте фазы.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
1) Мгновенное значение на векторной диаграмме определяется как проекция радиус –вектора на ось ординат  .
.
2) Обычно векторные диаграммы для удобства строятся не для амплитудных, а для действительных значений.
3) Начальная фаза на векторной диаграмме определяется углом между радиус-вектором и осью абсцисс. Если угол отсчитывают от оси абсцисс к вектору по направлению вращения, начальная фаза положительна.
4) Сдвиг фаз на векторной диаграмме определяется углом между векторами напряжения и тока. Если угол отсчитывается от тока к напряжению по направлению вращения, то сдвиг фаз положителен.
| Напряжение опережает ток | Ток опережает напряжение |

| 
|
| φ = + 75° - RL | φ = - 90° - RC |
Применение комплексных чисел для анализа электрических цепей переменного тока (символический метод).
Комплексное число – это сумма действительного и мнимого чисел.  , где
, где  и
и  - действительные числа,
- действительные числа,  - мнимая единица.
- мнимая единица.
На комплексной плоскости (Im÷ Re или j÷ 1) комплексное число может быть представлено либо точкой с координатами её проекций на оси Im÷ Re, либо вектором, соединяющим начальную координату с этой точкой.
 α – фаза.
α – фаза. 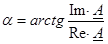 .
. 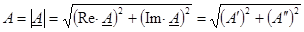 .
.
В электротехнике любая синусоидальная величина (ток, напряжение, ЭДС) по известной амплитуде и фазе ( ) на комплексной плоскости может быть представлена одним из трёх способов. Синусоидальные величины обозначают:
) на комплексной плоскости может быть представлена одним из трёх способов. Синусоидальные величины обозначают:  , комплексное число:
, комплексное число:  .
.
1) Алгебраический.
 ,
,  .
.

 .
.
Используется при сложении и вычитании комплексных чисел.
2) Тригонометрический.
 .
.
Используется для перехода от алгебраической к операторной форме записи и обратно.
3) Операторная (показательная) форма.
Формула Эйлера: 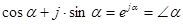 , где
, где 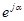 - оператор поворота,
- оператор поворота, 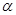 - фаза.
- фаза.
 ,
,  . Используется при делении и умножении комплексных чисел.
. Используется при делении и умножении комплексных чисел.
Особенности комплексной записи в электротехнике.
1. Мгновенное значение синусоидальной величины определяется как мнимая часть комплексного числа.
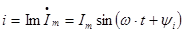 .
.  - комплексная амплитуда тока,
- комплексная амплитуда тока, 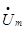 - комплексная амплитуда напряжения.
- комплексная амплитуда напряжения.
2. Для удобства комплексы синусоидальных величин используются не для амплитудных, а для действующих значений.
 - комплексное действительное значение тока (комплекс тока).
- комплексное действительное значение тока (комплекс тока).
 - комплексное действительное значение напряжения (комплекс напряжения).
- комплексное действительное значение напряжения (комплекс напряжения).
 .
.
3. Для упрощения записи принимаем t=0.  .
.
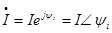 - комплекс тока.
- комплекс тока.
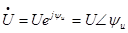 - комплекс напряжения.
- комплекс напряжения.
4. Для характеристики электрической цепи переменного тока вводится понятие комплексного сопротивления ( ) – это отношение комплекса напряжения к комплексу тока.
) – это отношение комплекса напряжения к комплексу тока. 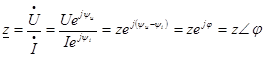 .
.
 ,
, 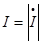 ,
,  - полное сопротивление.
- полное сопротивление.  .
.  - сдвиг фаз.
- сдвиг фаз.
5.  ,
,  - действительная часть комплексного сопротивления,
- действительная часть комплексного сопротивления,  - мнимая часть комплексного сопротивления (реактивное сопротивление (реактивная составляющая)).
- мнимая часть комплексного сопротивления (реактивное сопротивление (реактивная составляющая)).  . Если реактивное сопротивление отрицательно, то цепь обладает емкостным характером, если положительно – то индуктивным.
. Если реактивное сопротивление отрицательно, то цепь обладает емкостным характером, если положительно – то индуктивным.
6. Электрическая мощность в комплексной форме определяется как произведение комплексного действительного значения напряжения (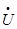 ) на сопряжённое комплексное действующее значение тока.
) на сопряжённое комплексное действующее значение тока.
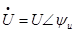 ,
,  ,
,  ,
,  .
. 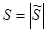 - полная мощность.
- полная мощность.
 ,
,
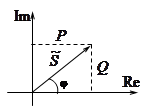
 ,
,  ,
,  .
.
Электрическая цепь переменного тока. Характеристики идеальных и реальных элементов цепи переменного тока. Условно-графические обозначения. Понятие об активной, реактивной и полной мощностях.
ОТВЕТ: В реальной цепи переменного тока происходит сложный энергетический процесс необратимого преобразования и периодического обмена электрической энергией. Для удобства и расчёта таких цепей составляют условные идеальные, так называемые, электрические схемы замещения (ЭСЗ или СЗ), которые полностью отражают электрофизические закономерности реальной цепи и составлены из так называемых идеальных электрических элементов.
Источники ЭДС и тока называются активными элементами, а резистивные, индуктивные и емкостные элементы – пассивными элементами схем замещения.
Идеальный электрический элемент – это участок идеальной электрической цепи (СЗ), выделенной условно-графическим обозначением (УГО) или буквенно-цифровым обозначением (БЦО), и в которой происходит только один энергетический процесс.
1. R – резистивный (активный) идеальный элемент. Отражает процесс необратимого преобразования электрической энергии в другие виды.
2. Х – реактивный идеальный элемент. Отражает процесс обмена электрической энергией между переменными электромагнитными полями реальной цепи (потребителя электроэнергии) и источником.
1) R. В нём отсутствуют переменные электромагнитные поля, что обозначает отсутствие обмена реактивной мощностью. Полное преобразование электроэнергии в другие виды энергии.

2) R. Различают два типа реактивных элементов: xL – индуктивный элемент, xC – емкостный элемент.
| Индуктивный элемент (идеальная катушка) | Емкостной элемент |
Индуктивный элемент характеризуется понятием индуктивность и связан с наличием переменного магнитного поля.  - индуктивность. - индуктивность. 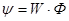 - магнитное потокосцепление, где - магнитное потокосцепление, где 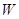 - число витков, - число витков,  - магнитный поток.
В простейшем случае индуктивность катушки определяют по следующей формуле: - магнитный поток.
В простейшем случае индуктивность катушки определяют по следующей формуле: 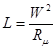 , ,  , где , где  - магнитная проницаемость среды, - магнитная проницаемость среды,  - длина и поперечное сечение магнитопровода катушки. - длина и поперечное сечение магнитопровода катушки.  . Наиболее просто и удобно применять индуктивность катушки за счёт изменения . Наиболее просто и удобно применять индуктивность катушки за счёт изменения  путём перемещения ферромагнитного сердечника катушки. путём перемещения ферромагнитного сердечника катушки. 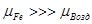 . .

| Характеризуется понятием «ёмкость» и характеризует процесс обмена электрической энергией между переменным электрическим полем емкостного элемента и источником.
Никакого преобразования электрической энергии не происходит.
Ёмкость:  , где , где  - заряд конденсатора, - заряд конденсатора, 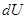 - напряжение на обкладках (зажимах) конденсатора.
В простейшем случае ёмкость плоско-параллельного конденсатора: - напряжение на обкладках (зажимах) конденсатора.
В простейшем случае ёмкость плоско-параллельного конденсатора:  , где , где  - диэлектрическая постоянная, - диэлектрическая постоянная,  - площадь пластин, - площадь пластин,  - расстояние между пластинами. - расстояние между пластинами.

|
Реальная катушка и реальный конденсатор (активно-индуктивный (R-L) и активно-емкостной (R-C) элементы в цепи переменного тока).
В любом электротехническом изделии, включённом в цепь переменного тока, происходит два энергетических процесса:
1. Процесс преобразования электроэнергии. Происходит в активном элементе R.
2. Периодический обратимый процесс обмена электроэнергией. Происходит в реактивном элементе x.
Поэтому любое электротехническое устройство на схеме может быть представлено как комбинация двух идеальных элементов.
z – реальное электротехническое устройство →  .
.
С целью упрощения ЭЦ в ряде случаев можно пренебречь наличием переменных электромагнитных полей (ЭМП). → Q=0 → x=0.
Примером такого устройства может служить резистор, лампа накаливания, нагревательный элемент. В этом случае:
1.  .
.
2. Если в электротехническом устройстве можно пренебречь тепловыми потерями (преобразованиями) электроэнергии, то → Р=0 → R=0, тогда:
 . Катушка рассматривается как идеальный индуктивный элемент.
. Катушка рассматривается как идеальный индуктивный элемент.
3. 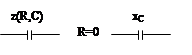 .
.
| R-L (реальная катушка) | R-С (реальный конденсатор) |
Реальная катушка наряду с индуктивность L, связанной с наличием переменного магнитного поля (ПМП), обладает активным сопротивлением, обусловленным сопротивлением провода ( ), из которого изготовлена катушка и на которой происходят Джоулиевы потери, вызывающие нагрев катушки, то есть: ), из которого изготовлена катушка и на которой происходят Джоулиевы потери, вызывающие нагрев катушки, то есть: 
| В реальном конденсаторе наряду с ёмкостью С, связанной с наличием переменного электрического поля (ПЭП), существуют тепловые потери элек5троэнергии в следствии переменной поляризации диэлектрика конденсатора и приводящие его к нагреванию. Эти тепловые потери на схеме можно представить в виде фиктивного элемента.  . .

|
| Уравнение электрического равновесия | |
 для действительного значения. для действительного значения.
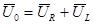

 , , 
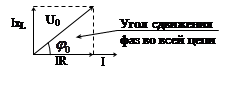
| 
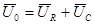

 , , 
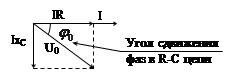
|
| Особенности цепи | |
| 1. Сдвиг фаз | |
В RL цепи:  Напряжение опережает ток.
Напряжение опережает ток.
| В RС цепи:  Ток опережает напряжение.
Ток опережает напряжение.
|
2. Коэффициент использования мощности (КИМ)  . .
| |
Характеризует степень преобразования электроэнергии в другие виды, то есть в работу как полную так и бесполезную. КИМ  . .
| |
| 3. Результирующая векторная диаграмма. | |
 , ,  . .

|  , , 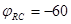 . Знак «-» обычно опускается и обозначает емкостной характер цепи. . Знак «-» обычно опускается и обозначает емкостной характер цепи.  . .

|
| 4. Треугольники напряжений, сопротивлений и мощности. | |
| Если вектор напряжения на векторной диаграмме (ВД) разложить на активную и реактивную составляющие, то получим треугольник напряжений. | |

| 
|
| Если напряжения поделить на ток, получим скалярный треугольник сопротивления R. | |

| 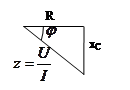
|
 , ,  , ,  , ,  , ,  , ,  . .
| |
| Если треугольник сопротивлений умножить на квадрат силы тока (I2), получим треугольник мощности. | |

| 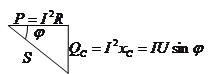
|
 , ,  , ,  , ,  , ,  , ,  . .
| |
5. Закон Ома.  , ,  . .
| |

| 
|
Произведение действующих значений напряжения между выводами источника  и тока источника
и тока источника  определяет так называемую полную мощность источника, равной полной мощности пассивного двухполюсника:
определяет так называемую полную мощность источника, равной полной мощности пассивного двухполюсника:  .
.
Процесс обмена энергией между источником энергии и совокупностью индуктивных и емкостных элементов пассивного двухполюсника отображается его реактивной мощностью, равной реактивной мощности источника:  .
.
Активная мощность двухполюсника и источника зависит от действующих значений напряжения и тока, а также от  - коэффициента мощности. Активная мощность пассивного двухполюсника всегда положительна и не зависит от знака угла
- коэффициента мощности. Активная мощность пассивного двухполюсника всегда положительна и не зависит от знака угла  (
( ). Она определяет энергетический режим пассивного двухполюсника в целом, то есть среднюю скорость необратимого преобразования энергии во всех резистивных элементах пассивного двухполюсника.
). Она определяет энергетический режим пассивного двухполюсника в целом, то есть среднюю скорость необратимого преобразования энергии во всех резистивных элементах пассивного двухполюсника.  ,
, 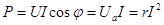 .
.
 .
.  .
.
Идеальные элементы (резистивный, индуктивный и емкостный) в цепи переменного тока. Определения, основные соотношения и особенности цепи. Понятие об активной, реактивной и полной мощностях.
| R-элемент | L-элемент | C-элемент |
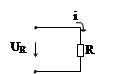
| 
| 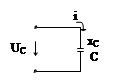
|
| 1. Отсутствуют переменные электромагнитные поля. 2. Происходит полное преобразование электроэнергии в работу. | 1. Отсутствует преобразование электроэнергии в другие виды (работу) | |
| 2. Происходит периодический обмен электроэнергией между переменным магнитным полем L-элемента и источником. | 2. Происходит периодический обмен электроэнергии между переменным электрическим полем и источником. | |
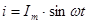 , ,  . По второму правилу Кирхгофа: . По второму правилу Кирхгофа: 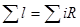 . .
| ||
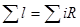 , , 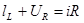 , ,  , так как отсутствует магнитное поле. , так как отсутствует магнитное поле. 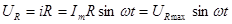 , ,
 . .
| 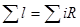 , , 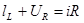 ( (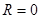 ), ),  , ,  , , 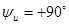 . .
| 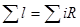 , , 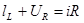 ( (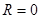 ), ), 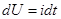 , ,  , ,
 . .
|
| Особенности цепи. | ||
1. Сдвиг фаз.  . .
| ||
 в резистивном элементе сдвиг фаз в резистивном элементе сдвиг фаз 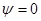 , то есть ток и напряжение совпадают по фазе. , то есть ток и напряжение совпадают по фазе.
| В индуктивном элементе сдвиг фаз 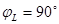 , то есть напряжение опережает ток на четверть периода. , то есть напряжение опережает ток на четверть периода.
| В емкостном элементе сдвиг фаз  , то есть напряжение отстаёт от тока на четверть периода. , то есть напряжение отстаёт от тока на четверть периода.
|
2. Коэффициент использования мощности  . Определяет степень преобразования электроэнергии в работу. . Определяет степень преобразования электроэнергии в работу.
| ||
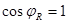 . Вся электрическая мощность преобразуется в работу. . Вся электрическая мощность преобразуется в работу.
| 
| 
|
| Преобразование электрической мощности не происходит. | ||
| 3. Закон Ома. | ||
 , ,  , ,  . .
|  , ,  , , 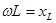 - индуктивное сопротивление. - индуктивное сопротивление.  , , 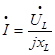 . .
|  , , 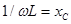 - емкостное сопротивление. - емкостное сопротивление.  , , 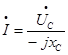 . .
|
| 4. Векторная диаграмма. | ||
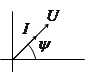
| 
| 
|
Произведение действующих значений напряжения между выводами источника  и тока источника
и тока источника  определяет так называемую полную мощность источника, равной полной мощности пассивного двухполюсника:
определяет так называемую полную мощность источника, равной полной мощности пассивного двухполюсника:  .
.
Процесс обмена энергией между источником энергии и совокупностью индуктивных и емкостных элементов пассивного двухполюсника отображается его реактивной мощностью, равной реактивной мощности источника:  .
.
Активная мощность двухполюсника и источника зависит от действующих значений напряжения и тока, а также от  - коэффициента мощности. Активная мощность пассивного двухполюсника всегда положительна и не зависит от знака угла
- коэффициента мощности. Активная мощность пассивного двухполюсника всегда положительна и не зависит от знака угла  (
( ). Она определяет энергетический режим пассивного двухполюсника в целом, то есть среднюю скорость необратимого преобразования энергии во всех резистивных элементах пассивного двухполюсника.
). Она определяет энергетический режим пассивного двухполюсника в целом, то есть среднюю скорость необратимого преобразования энергии во всех резистивных элементах пассивного двухполюсника.  ,
, 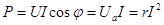 .
.
 .
.  .
.
|
|
