Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Критерий устойчивости Г. Найквиста.

Критерии Гурвица, Рауса и Михайлова дают оценку устойчиво­сти именно той системы (замкнутой или разомкнутой), характеристи­ческое уравнение которой анализируется. По сравнению с ними кри­терий Найквиста имеет следующие особенности:

- по характеристикам разомкнутой системы судят об устойчивости системы после ее замыкания;

- для анализа используют передаточную функцию целиком, а не толь­ко ее знаменатель;

- для анализа можно использовать не расчетную, а экспериментально полученную АФЧХ разомкнутой системы;

- можно исследовать по имеющимся АФЧХ системы с запаздыванием.

Критерий Найквиста – это частотный критерий, позволяющий судить об устойчивости САУ, замкнутой единичной обратной связью, по виду амплитудно-фазовой частотной характеристики разомкнутой системы.

Для формулировки критерия рассмотрим САУ, которая в разомкнутом состоянии характеризуется передаточной функцией вида

,

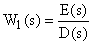где 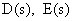– некоторые полиномы от , причем степень знаменателя выше или равна степени числителя.

Знаменатель этого выражения является характеристическим полиномом разомкнутой САУ. Передаточная функция такой системы, охваченной 100% отрицательной обратной связи, определяется как

,

где – характеристический полином замкнутой систем.

Обратное этому выражение определяется как

.

Обозначим корни характеристического уравнения разомкнутой системы – .

Корни характеристического уравнения замкнутой системы обозначим как — .

В плоскости корней, каждый корень может быть представлен вектором, проведенным из начала координат. Если выбрать значение независимой переменной в произвольной точке комплексной плоскости, то комплексное число вида 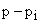может быть представлено в виде разностного вектора, как показано на рис. 10.1.

Рис.10.1. Графическое представление разности векторов

Если 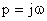, то разностный вектор будет иметь свое начало в точке окончания вектора 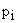, а окончание – на мнимой оси. В этом случае выражение для обратной передаточной функции замкнутой САУ можно представить как

При изменении частоты от до будет скользить по мнимой оси и повернется на угол 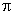. Поворот будет происходить против часовой стрелки, если корень лежит слева от мнимой оси, и по часовой стрелке, если корень расположен в правой полуплоскости. Числитель и знаменатель этого выражения могут быть представлены как некоторые вектора, модуль которых равен произведению модулей сомножителей, а угол поворота – как сумма углов поворота векторов сомножителей. Поэтому можно записать, что

Таким образом полный угол поворота рассматриваемого вектора при изменении частоты от до равен разности углов поворота векторов 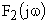и . Для САУ устойчивой в разомкнутом состоянии все корни характеристического полинома лежат в левой полуплоскости. Поэтому суммарный угол поворота вектора знаменателя при изменении частоты от до равен n .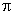

В общем случае характеристический полином замкнутой САУ имеет корней в правой полуплоскости и корней в левой полуплоскости. Поэтому суммарный угол поворота вектора числителя при изменении частоты от до равен или . Суммарный угол поворота вектора будет определяться как

.

Для устойчивой САУ все корни характеристического полинома должны располагаться в левой полуплоскости, то есть . Следовательно суммарный угол поворота вектора устойчивой системы при рассмотренных ранее условиях равен нулю. То есть будет выполняться условие

.

При выполнении этого условия вектор будет располагаться справа от мнимой оси. Этот вектор определяется АФЧХ разомкнутой САУ, но его начало находится в точке (–1, j0). Исходя из этого, формулируется критерий устойчивости Найквиста.

Формулировка критерия. САУ устойчива в замкнутом состоянии, если годограф АФЧХ устойчивой разомкнутой системы не охватывает точки с координатами (-1, j0) на комплексной плоскости. Эта формулировка справедлива как для статических, так и астатических САУ, то есть систем, характеристическое уравнение которых содержит нулевой корень той или иной степени кратности.

На рис. 10.2 приведены АФЧХ устойчивых и неустойчивых САУ.

Устойчивые САУ Неустойчивые САУ

Рис. 10.2. АФЧХ устойчивых и неустойчивых САУ