Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Вказівки до виконання роботи. Перед виконанням лабораторної роботи необхідно вивчити такий теоретичний матеріал: малі коливання; математичний маятник; фізичний маятник

Перед виконанням лабораторної роботи необхідно вивчити такий теоретичний матеріал: малі коливання; математичний маятник; фізичний маятник. Згасаючі гармонійні коливання. Характеристики згасання.

Фізичний маятник − це тіло, що має змогу обертатись навколо нерухомої горизонтальної осі, яка не проходить через центр мас тіла (рис. 4.1.1). При відхиленні маятника на кут j від положення рівноваги виникає обертовий момент M, який прагне повернути маятник у положення рівноваги:

, (4.1.1)

де m − маса тіла; ℓ − відстань від осі обертання до центра мас маятника.

Якщо маятник відпустити з такого положення, то виникне коливальний рух. Коливальному руху маятника перешкоджають опір повітря і тертя в осі маятника. Відомо, що у випадку невеликої швидкості руху сумарний момент сил опору буде пропорційний кутовій швидкості руху маятника:

, (4.1.2.)

де – коефіцієнт опору навколишнього середовища; − кутова швидкість. Знак “-“ свідчить про те, що вектори та мають протилежний напрям.

Отже, рівняння руху фізичного маятника, записане на основі динаміки обертального руху абсолютно твердого тіла відносно закріпленої осі при наявності опору середовища, буде мати вигляд:

, (4.1.3)

де J – момент інерції маятника відносно осі обертання; − кутове прискорення.

Враховуючи, що при малих кутах відхилення , а також вводячи позначення та , рівняння руху можна записати у вигляді:

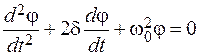. (4.1.4)

Розв’язком цього рівняння є функція залежності кута обертання маятника від часу, яку записують у вигляді:

. (4.1.5)

Виходячи з вигляду цієї функції, рух маятника можна розглядати як гармонійне коливання з частотою та амплітудою, яка змінюється з часом за законом .

Період згасаючих коливань дорівнює:

. (4.1.6)

Якщо коефіцієнт опору середовища невеликий, тобто можна вважати його рівним нулю ( =0), то це означає, що і d=0. Тоді формула періоду коливань запишеться так:

. (4.1.7)

Швидкість згасаючих коливань характеризується коефіцієнтом згасання d. Для визначення коефіцієнта згасання користуються залежністю амплітуди від часу, яка подається у вигляді логарифмічної функції:

. (4.1.8)

У координатах () рівняння (4.1.8) є прямою лінією. Величина d визначає кутовий коефіцієнт нахилу прямої (4.1.8) до осі часу t (рис. 4.1.3):

або . (4.1.9)

Якщо , то .

З останньої формули можна дати таке визначення коефіцієнта згасання: значення коефіцієнта згасання d є величиною, оберненою до проміжку часу t_e, амплітуда коливань якого згодом зменшується в е =2, 71828…раз. Співвідношення (4.1.9) можна використовувати для експериментального визначення d.

Крім коефіцієнта згасання для характеристики згасання застосовують також логарифмічний декремент згасання , який визначається логарифмом відношення амплітуд, що відповідають моментам часу, які відрізняються на період:

. (4.1.10)

Фізичний маятник виконано у вигляді металевого стрижня 1 (рис. 4.1.4), до верхнього торця якого прикріплено дві призми. Ці призми спираються своїми ребрами на раму. Для зміни періоду коливань на стрижень надітий масивний вантаж 2, положення якого можна регулювати гвинтами. Відлік амплітуди коливань у градусах виконується за шкалою 3.