Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

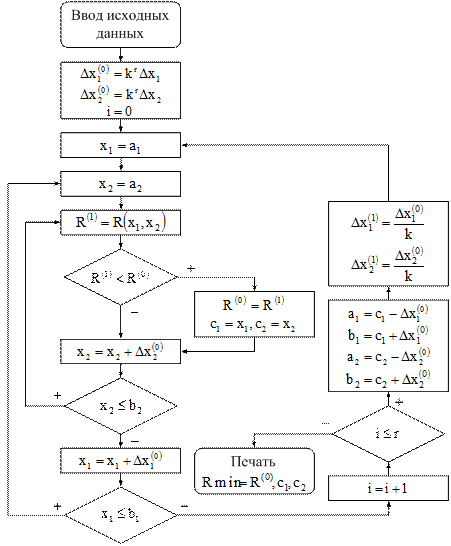
Алгоритм метода сканирования с переменным шагом

Рассмотрим случай, когда число независимых переменных равно двум, задана область изменения независимых переменных:

, .

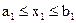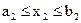1. В качестве первого приближения минимального значения целевой функции примем .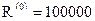

2. Определяем начальный шаг сетки переменных

,

,

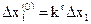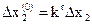где 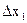, 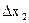– точность определения оптимума, r – число этапов уточнения поиска, на которых шаг поиска уменьшается в k раз.

3. Разбиваем область изменения независимых переменных с шагом 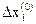, 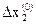на совокупность точек, значение целевой функции в которых вполне определяют ее поведение.

4. Определяем значение целевой функции в узлах сетки переменных. Пусть 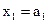. Для каждого значения 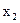из интервала 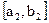при 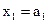определяем значение целевой функции.

Изменяем значение переменной 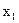на шаг 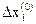и при новом значении 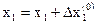для каждого значения 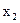из интервала 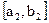вычисляем значение целевой функции. Аналогичным образом исследуем весь диапазон изменения переменных.

Находим значение целевой функции в узлах сетки переменных.

5. В результате грубого поиска определяем узел 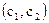, в котором значение целевой функции наименьшее (наибольшее).

6. Определяем область изменения независимых переменных, в пределах которой будем уточнять значение оптимума целевой функции.

, ,

, .

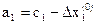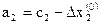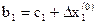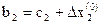7. Производим сканирование новой области с меньшим шагом

,

,

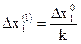где 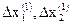– шаг уточнения, с которым исследуется новая область.

8. Определяем значения целевой функции в узлах новой сетки переменных вышеизложенным способом.

Находим узел, в котором значение целевой функции наименьшее (наибольшее). Если более не предусмотрено этапов уточнения, то найденное значение целевой функции будет оптимальным.

Блок – схема алгоритма решения задачи методом сканирования