💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Алгоритм. Свойства алгоритма. Формы представления алгоритмов.

Моделирование как метод научного познания. Классификация моделей.

Модели – представления объектов или процессов реального или вымышленного мира.

Виды моделей: графические представления, натурные, математические, информационно–логические и т.п.

Графические представления – графические изображения объектов и процессов.

Свойства моделей: адекватность, полнота, детальность и т.п.

Адекватность – степень соответствия модели представляемым объектам.

Математическая модель – это совокупность математических объектов (данных) и отношений между ними, отражающих некоторые свойства моделируемого процесса.

Информационно–логические модели – формальные описания объектов, допускающие их представление и обработку на ЭВМ.

Модели движения бывают аналитические, дифференциальные, разностные.

Этапы решения задач на ЭВМ.

Решение задач с помощью компьютера включает в себя следующие основные этапы, часть из которых осуществляется без участия компьютера:

1. Постановка задачи: сбоp инфоpмации о задаче, фоpмулиpовка условия задачи, опpеделение конечных целей pешения задачи, определение формы выдачи результатов, описание данных.
2. Анализ и исследование задачи, модели.
3. Разработка алгоритма.

С участием компьютера:

1. Запись алгоpитма на выбpанном языке пpогpаммиpования.
2. Тестиpование и отладка.
3. Анализ результатов решения задачи и уточнение в случае необходимости математической модели с повторным выполнением этапов 1-2.
4. Сопровождение программы:
• доработка программы для решения конкретных задач;
• составление документации к решенной задаче, к математической модели, к алгоритму, к программе, к набору тестов, к использованию.

Математическая модель.

Математическая модель – это система математических соотношений – формул, уравнений, неравенств и т.д., отражающих существенные свойства объекта или явления.

Чтобы описать явление, необходимо выявить самые существенные его свойства, закономерности, внутренние связи, роль отдельных характеристик явления. Выделив наиболее важные факторы, можно пренебречь менее существенными.

Создавая математическую модель для решения задачи, нужно:

· выделить предположения, на которых будет основываться математическая модель;

· определить, что считать исходными данными и результатами;

· записать математические соотношения, связывающие результаты с исходными данными.

Алгоритмизация.

Алгоритм. Свойства алгоритма. Формы представления алгоритмов.

Алгоритм – точное и понятное предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи.

Основные свойства алгоритмов:

1. Понятность для исполнителя.
2. Дискретность (прерывность, раздельность) – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов (этапов).
3. Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола.
4. Результативность – это свойство состоит в том, что алгоритм должен приводить к решению задачи за конечное число шагов.
5. Массовость. Алгоритм решения задачи pазpабатывается в общем виде.

Формы представления алгоритмов:

• словесная (записи на естественном языке);

• графическая (изображения из графических символов);

• псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке;

• программная (тексты на языках программирования).

Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных.

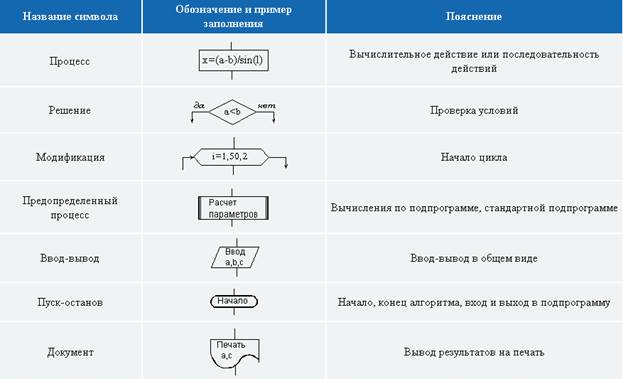
Графическом представление – алгоритм изображается в виде последовательности связанных между собой функциональных блоков.

Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.

В таблице приведены наиболее часто употребляемые символы: