Постановка и геометрическая интерпретация задачи параметрического программирования

Обобщением задач линейного программирования являются задачи параметрического программирования. Данными задач параметрического программирования являются не постоянные величины, а функции, определенным образом зависящие от некоторых детерминантных параметров, в этом и заключается обобщение. Предположим, например, что изготовленная заводом продукция подлежит хранению, то ее цена будет определяться из двух компонентов: 1) постоянной, зависящей от стоимости продукции на момент изготовления; 2) переменной, имеющую зависимость от срока хранения продукции. Линейную форму задачи оптимального планирования этого производства можно сформулировать через коэффициенты, линейно зависимые от единого параметра, в частности от времени .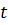

Нередко на практике встречаются задачи, где в целевой функции значения коэффициентов известны приближенно. Таким образом, можно узнать поведение решений задач при разных значениях этих коэффициентов, представив их в форме линейных функций параметра 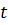. Подобно можно провести исследование для случая, когда меняются коэффициенты системы ограничений.

Рассмотрим целевую функцию, где коэффициенты зависят от параметра. В этом случае, математически, задачу представляют так: пусть параметр 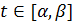, где 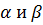— действительные числа. Необходимо найти для каждого 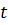на отрезке свой вектор

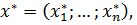максимизирующий

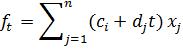(1.1)

при условиях

(1.2)

В функции (1.1) 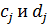известные константы.