Численный метод решения задачи

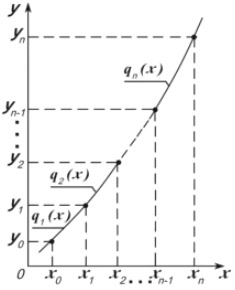
Значения f(x₀ ), f(x₁ ), … , f(x_n ) , т.е. значения табличной функции в узлах, называются разделенными разностями нулевого порядка (k=0).

Отношение 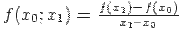называется разделенной разностью первого порядка (k=1) на участке [x₀ , x₁ ] и равно разности разделенных разностей нулевого порядка на концах участка [x₀ , x₁ ], разделенной на длину этого участка.

Для произвольного участка [x_i , x_i+1 ] разделенная разность первого порядка (k=1) равна

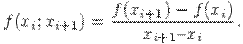
Отношение 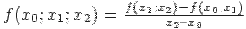называется разделенной разностью второго порядка (k=2) на участке [x₀ , x₂ ] и равно разности разделенных разностей первого порядка, разделенной на длину участка [x₀, x₂ ].

Для произвольного участка [x_i , x_i+2 ] разделенная разность второго порядка (k=2) равна

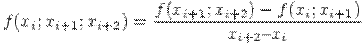
Таким образом, разделенная разность k-го порядка на участке [x_i , x_i+k ] может быть определена через разделенные разности (k-1)-го порядка по рекуррентной формуле:

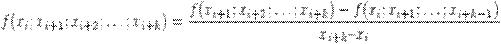(2.3)

Где 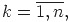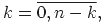n – степень многочлена.

Максимальное значение k равно n. Тогда i =0 и разделенная разность n-го порядка на участке [x₀ ,x_n ] равна

,

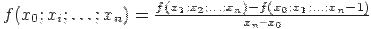т.е. равна разности разделенных разностей (n-1)-го порядка, разделенной на длину участка [x₀ ,x_n ].

Разделенные разности

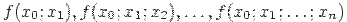
являются вполне определенными числами, поэтому выражение (2.2) действительно является алгебраическим многочленом n-й степени. При этом в многочлене (2.2) все разделенные алгебраическим многочленом n-й степени. При этом в многочлене (2.2) все разделенные разности определены для участков [x₀ , x_0+k ], .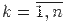

Лемма: алгебраический многочлен (2.2), построенный по формулам Ньютона, действительно является интерполяционным многочленом, т.е. значение многочлена в узловых точках равно значению табличной функции

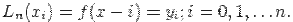
Докажем это. Пусть х=х₀ , тогда многочлен (2.2) равен

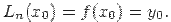
Пусть х=х₁ , тогда многочлен (2.2) равен

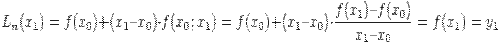
Пусть х=х₂ , тогда многочлен (2.2) равен

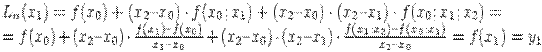
Заметим, что решение задачи интерполяции по Ньютону имеет некоторые преимущества по сравнению с решением задачи интерполяции по Лагранжу. Каждое слагаемое интерполяционного многочлена Лагранжа зависит от всех значений табличной функции y_i , i=0,1,…n. Поэтому при изменении количества узловых точек N и степени многочлена n (n=N-1) интерполяционный многочлен Лагранжа требуется строить заново. В многочлене Ньютона при изменении количества узловых точек N и степени многочлена n требуется только добавить или отбросить соответствующее число стандартных слагаемых в формуле Ньютона (2.2). Это удобно на практике и ускоряет процесс вычислений.