Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Билет №9. Задачи линейной теории автоматического управления. Уравнения динамики САУ и их решение.
|
|
1.Изучение динамических свойств и характеристик различных звеньев автоматических систем любой физической природы. 2.Формирование функциональных и структурных схем САУ. 3.Построение динамических характеристик САУ. 4.Определение показателей точности и ошибок САУ.5.Исследование устойчивости САУ.6.Оценка качественных показателей процесса управления. 7.Изучение различных видов корректирующих устройств вводимых в САУ для повышения точности и улучшения динамических свойств.
Уравнения динамики САУ и их решение: Исследование переходных процессов САУ основывается на использовании дифференциальных уравнений при изучении динамических процессов САУ. При этом отвлекаются от конкретной физической природы процессов, а используют лишь их математическую модель. В основе построения математической модели лежит ее структурная схема, состоящая из типовых математических звеньев. В свою очередь каждое типовое динамическое звено описывается дифференциальными или операторными уравнениями, которые описывают физическую природу происходящих в них процессах.
dx/dt+dy/dt=0 Процесс дифференцирования Лаплас предложил заменить функцией P=d/dt оператор Лапласа, а процесс интегрирования на 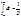 , получил: px+py=0
, получил: px+py=0
Одно конкретное устройство САУ (электродвигатель, реле, трансформатор) описывается одним дифференциальным уравнением.
Совокупность нескольких дифференциальных уравнений динамических звеньев представляет собой математическую модель всей системы и служит для получения общего характеристического уравнения системы в целом.
Аналитические методы расчета основаны на использовании классических или операторных методах:
1.Классическое вариационное исчисление. 2.Принцип максимума Л.С.Понтрягина. 3.Метод динамического программирования Р.Беллмана.
Билет № 10.Основные типы входных воздействий для исследования САУ.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Для исследования динамических свойств САУ используют следующие типовые сигналы:
1.Ступенчатый. 2.Импульсный. 3.Гармонический. 4.Линейно- нарастающий. 5.Прямоугольный.
Ступенчатый сигнал наиболее простой - функция времени, которая в момент времени t0=0 и достигает значения a=const и далее остается постоянным
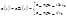
1(t)-единичная функция времени
Импульсный сигнал - предел прямоугольного импульса высотой h и длительностью Δ t при 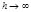 и
и 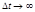 .
.
Площадь импульса определяется 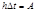 , при этом сигнал представляет собой производную от ступенчатого сигнала и описывается по формуле:
, при этом сигнал представляет собой производную от ступенчатого сигнала и описывается по формуле:
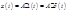
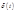 - функция Дирана
- функция Дирана
Гармонический сигнал 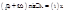
Линейно-нарастающий 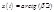
Прямоугольный импульс (то же что и ступенчатый, только заканчивается).

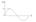


 Динамические характеристики отображают переходные процессы в системе при различных формах воздействия и определяются с использованием соответствующих сигналов:
Динамические характеристики отображают переходные процессы в системе при различных формах воздействия и определяются с использованием соответствующих сигналов:
1.Ступенчатый сигнал- для получения переходной характеристики. 2.Импульсный сигнал - для получения весовой характеристики. 3.Гармонический сигнал- при исследовании частотных свойств сигнала. 4.Линейно-нарастающий – при исследовании динамики следящих систем.
Прямоугольный сигнал – при построении комплексной характеристики САУ.
Билет № 12. Типовое динамическое звено, определение. Основные хар-ки звена.
САУ любой сложности может быть представлена из совокупности типовых динамических звеньев. Различат несколько десятков типовых динамических звеньев, основные из них следующие: 1.Без инерционное (усилительное) звено.2.Идеальное интегрирующее звено.3.Идеальное дифференцирующее звено. 4.Апериодическое 1-го и 2-го порядка звено. 5.Колебательное звено. 6.Реальное интегрирующее звено. Каждое типовое динамическое звено описывается своими собственными характеристикам: 1.Передаточная функция звена ω (p)=y(p)/x(p) Показывает отношение операторного изображения выходной величины к операторному изображению входной величины.
2.Переходная характеристика y(t)-показывает качество переходного процесса. 3.Весовая функция h(t)-показывает реакцию звена на единичное импульсное воздействие. 4.Амплитудно-частотная характеристик А(ω)- показывает зависимость амплитуды выходного сигнала от частоты входного. 5.Фазо-частотная характеристика φ (ω)- показывает зависимость фазы выходного сигнала от частоты входного. 6.Комплексная характеристика ω (ω j) - показывает границы и запас устойчивости работы звена.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
 ПП – переходный процесс
Исходя из вида переходных процессов, все САУ делятся:
1.Устойчивые САУ- при изменении входных сигналов, регулируемая величина переходит в новое заданное состояние и поддерживается сколь угодно долго.
ПП – переходный процесс
Исходя из вида переходных процессов, все САУ делятся:
1.Устойчивые САУ- при изменении входных сигналов, регулируемая величина переходит в новое заданное состояние и поддерживается сколь угодно долго.
 2.Неустойчивые САУ- вызывают изменение регулируемой величины во времени без ее стабилизации.
3.Консервативные СА- система находится на грани устойчивости.
В зависимости от заданного режима САУ должна обеспечивать требуемое количество работы в переходных режимах вызванных изменением задающего параметра x(t) или возмущающего f(t).
Качество регулирования оцениваются следующими основными показателями:
Величина перерегулирования - отношение а1 к а2 определяет величину перерегулирования
а1 > а2 – затухающий процесс (чем больше разница, тем больше коэффициент затухания).
а1 < а2 -расходящийся процесс, САУ неустойчивая.
а1 = а2 автоколебательный процесс, коэффициент затухания равен нулю.
2.Время переходного процесса tпп чем меньше этот промежуток, тем быстрее осуществляется реакция системы на изменение входных сигналов.
Длительность переходных процессов определяется зоной статической ошибки-
2.Неустойчивые САУ- вызывают изменение регулируемой величины во времени без ее стабилизации.
3.Консервативные СА- система находится на грани устойчивости.
В зависимости от заданного режима САУ должна обеспечивать требуемое количество работы в переходных режимах вызванных изменением задающего параметра x(t) или возмущающего f(t).
Качество регулирования оцениваются следующими основными показателями:
Величина перерегулирования - отношение а1 к а2 определяет величину перерегулирования
а1 > а2 – затухающий процесс (чем больше разница, тем больше коэффициент затухания).
а1 < а2 -расходящийся процесс, САУ неустойчивая.
а1 = а2 автоколебательный процесс, коэффициент затухания равен нулю.
2.Время переходного процесса tпп чем меньше этот промежуток, тем быстрее осуществляется реакция системы на изменение входных сигналов.
Длительность переходных процессов определяется зоной статической ошибки-
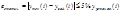
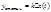 k-коэффициент усиления САУ
3.Быстродействие системы- определяется промежутком времени от начала действия входного сигнала до момента первого пересечения линии yуст, определяет чувствительность системы
4.Собственная частота колебаний системы
k-коэффициент усиления САУ
3.Быстродействие системы- определяется промежутком времени от начала действия входного сигнала до момента первого пересечения линии yуст, определяет чувствительность системы
4.Собственная частота колебаний системы
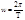 Т- постоянная времени судна
Т- постоянная времени судна
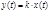 , где К - коэффициент усиления
, где К - коэффициент усиления
 1.Передаточная функция звена
1.Передаточная функция звена
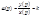 2. Переходная характеристика
2. Переходная характеристика
 Для исследования переходной характеристики используется ступенчатый сигнал.
3. Весовая характеристика
Весовая характеристика показывает отсутствие реакции на единичное импульсное воздействие (обладает нулевой инерционностью)
4.Амплитудно-частотная характеристика - д анное звено обладает нулевой инерционностью.
Для исследования переходной характеристики используется ступенчатый сигнал.
3. Весовая характеристика
Весовая характеристика показывает отсутствие реакции на единичное импульсное воздействие (обладает нулевой инерционностью)
4.Амплитудно-частотная характеристика - д анное звено обладает нулевой инерционностью.
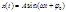
 , где
, где  - действительная часть
- действительная часть 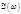 - мнимая часть характеристики.
Амплитудно-частотная характеристика показывает, что амплитуда выходного сигнала постоянна для всего диапазона частот и определяется коэффициентом усиления. Данное звено не вносит никаких изменений в форму сигнала.
5. Фазо-частотная характеристика
- мнимая часть характеристики.
Амплитудно-частотная характеристика показывает, что амплитуда выходного сигнала постоянна для всего диапазона частот и определяется коэффициентом усиления. Данное звено не вносит никаких изменений в форму сигнала.
5. Фазо-частотная характеристика
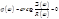 Фазо-частотная характеристика показывает что для выходного сигнала отсутствует фазовый сдвиг для всего диапазона частот.
Фазо-частотная характеристика показывает что для выходного сигнала отсутствует фазовый сдвиг для всего диапазона частот.
 6. Комплексная характеристика
6. Комплексная характеристика 



 Данное звено обладает неограниченным запасом устойчивости по амплитуде входного сигнала. Примеры безинерционного усилительного звена: выключатель, реле, трансформатор.
Данное звено обладает неограниченным запасом устойчивости по амплитуде входного сигнала. Примеры безинерционного усилительного звена: выключатель, реле, трансформатор.
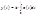 1.Передаточная функция звена
1.Передаточная функция звена
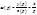 2.Переходная характеристика
2.Переходная характеристика
 характеристика показывает, что на выходе звена идет накопление сигналов.
3. Весовая характеристика
Весовая характеристика показывает отсутствие реакции на единичное импульсное воздействие (обладает нулевой инерционностью)
4. Амплитудно-частотная характеристика
Амплитудно-частотная характеристика показывает, что чем меньше частота, тем больше всплеск амплитуды на выходе.
5.Фазо-частотная характеристика
характеристика показывает, что на выходе звена идет накопление сигналов.
3. Весовая характеристика
Весовая характеристика показывает отсутствие реакции на единичное импульсное воздействие (обладает нулевой инерционностью)
4. Амплитудно-частотная характеристика
Амплитудно-частотная характеристика показывает, что чем меньше частота, тем больше всплеск амплитуды на выходе.
5.Фазо-частотная характеристика
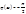 Фазовый сдвиг постоянен для всего диапазона частот.
6. Комплексная характеристика
Фазовый сдвиг постоянен для всего диапазона частот.
6. Комплексная характеристика

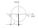

 Согласно критериям Найквеста, данное звено обладает запасом устойчивости по фазе входного сигнала
Согласно критериям Найквеста, данное звено обладает запасом устойчивости по фазе входного сигнала 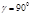 и запасом устойчивости по амплитуде h. Пример: курс судна на циркуляции, конденсатор и т.д.
и запасом устойчивости по амплитуде h. Пример: курс судна на циркуляции, конденсатор и т.д.
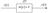
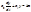 , где a0 a1 b - параметры звена.
Для получения передаточной функции используем преобразование Лапласа и разделим все уравнение на a1, в результате получим:
, где a0 a1 b - параметры звена.
Для получения передаточной функции используем преобразование Лапласа и разделим все уравнение на a1, в результате получим:
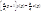 Вводим замену переменных:
a0/a1=T, где Т – постоянная времени звена.
B/a1=K, где К – коэффициент усиления.
Получаем:
(Tp+1)y(p)=K*x(p)
Вводим замену переменных:
a0/a1=T, где Т – постоянная времени звена.
B/a1=K, где К – коэффициент усиления.
Получаем:
(Tp+1)y(p)=K*x(p)
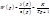 2. Переходная характеристика
3Т – длительность процесса
2. Переходная характеристика
3Т – длительность процесса
 3. Весовая характеристика
Весовая характеристика показывает, что апериодическое звено первого порядка обладает инерционностью. Данная характеристика показывает чувствительность звена при единичном импульсном воздействии.
4. Амплитудно-частотная характеристика
3. Весовая характеристика
Весовая характеристика показывает, что апериодическое звено первого порядка обладает инерционностью. Данная характеристика показывает чувствительность звена при единичном импульсном воздействии.
4. Амплитудно-частотная характеристика
 При w®¥, A(w)®0
При частотах близким к нулевым, максимальное значение амплитуды не превышает значения К.
5. Фазо-частотная характеристика
j(w)=-arctg(T*w)
6. Комплексная характеристика
w (jw)=A(w)*j(w)
При w®¥, A(w)®0
При частотах близким к нулевым, максимальное значение амплитуды не превышает значения К.
5. Фазо-частотная характеристика
j(w)=-arctg(T*w)
6. Комплексная характеристика
w (jw)=A(w)*j(w)
 Точка пересечения годографа и единичной окружности является характеристической точкой и вектор, проведенный из центра в эту точку, определяет запас устойчивости по фазе входного сигнала g, а расстояние от крайней левой точки годографа до точки -1j0 называется h и определяет запас устойчивости по амплитуде входного сигнала. Другими словами годограф комплексной характеристики показывает границу устойчивости работы звена.
Точка пересечения годографа и единичной окружности является характеристической точкой и вектор, проведенный из центра в эту точку, определяет запас устойчивости по фазе входного сигнала g, а расстояние от крайней левой точки годографа до точки -1j0 называется h и определяет запас устойчивости по амплитуде входного сигнала. Другими словами годограф комплексной характеристики показывает границу устойчивости работы звена.

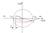 Система автоматического управления будет устойчива в том случае, если годограф передаточной функции не охватывает точку [-1; j0]. В противном случае система не устойчива.
Если через точку с координатами [-1; j0] провести окружность единичного радиуса с центром в точке [0; 0], то получим точку пересечения годографа передаточной функции с окружностью (точка А). Угол γ определяет запас устойчивости системы по фазе входного сигнала (x(t) и f(t)). Запас устойчивости по модулю амплитуды входного сигнала определяется отрезком h, который ограничивает устойчивость системы в целом.
Особенности критерия:
Система автоматического управления будет устойчива в том случае, если годограф передаточной функции не охватывает точку [-1; j0]. В противном случае система не устойчива.
Если через точку с координатами [-1; j0] провести окружность единичного радиуса с центром в точке [0; 0], то получим точку пересечения годографа передаточной функции с окружностью (точка А). Угол γ определяет запас устойчивости системы по фазе входного сигнала (x(t) и f(t)). Запас устойчивости по модулю амплитуды входного сигнала определяется отрезком h, который ограничивает устойчивость системы в целом.
Особенности критерия:
 Различают характеристики первого и второго рода. а) характеристика первого рода называется годограф пересекающий ось абсцисс справа от точки [-1; j0]
График устойчивой системы второго рода.
б) График неустойчивой системы.
Различают характеристики первого и второго рода. а) характеристика первого рода называется годограф пересекающий ось абсцисс справа от точки [-1; j0]
График устойчивой системы второго рода.
б) График неустойчивой системы.
 В случае, если годограф передаточной функции проходит через точку [-1; j0], то система находится на грани устойчивости (консервативная система)
Вопрос№22
Данные системы характеризуются тем, что управляющий алгоритм автоматически, целенаправленно изменяется для достижения успешного или в каком-либо смысле оптимального управления.
Все адаптивные САУ делятся на 3 вида:
Самонастраивающаяся система – адаптация в данной системе осуществляется путем изменения параметров управляющих воздействий
Самоорганизующаяся система – система, в которой адаптация осуществляется путем изменения не только параметров u(t), но и структура управляющего устройства. (т.е. меняется алгоритм обработки результатов измерений).
Самообучающаяся САУ – это САУ, в которой оптимальный режим работы объекта управления определяется при помощи управляющего устройства, алгоритм которого автоматически целенаправленно совершенствуется в процессе обучения, путем автопоиска. При этом при выборе решения, система автоматически запоминает все предыдущие состояния.
Вопрос№25
Особенности решения навигационной задачи с использованием вероятностных алгоритмов обработки результатов измерений.
Основное содержание заключается в определении координат и скоростей объекта являющихся основой их вектора состояния. X=[φ; λ; Δ B]
- географическая система координат низкоскоростных объектов. x=[x, y, z, x, ỳ, z, Δ B, Δ B] - для высокоскоростных объектов
Для нахождения данных величин, используют алгоритмы, которые отличаются ходом вычислительного процесса. На практике используются итерационные алгоритмы. В основу метода статистического оценивания могут быть положены следующие критерии качества оптимизации:
1.минимум дисперсии ошибок оценки вектора состояния
2.минимум суммы модуля невязок
3.максимум функций правдоподобия
4.максимум плотности апостериорной вероятности
Уравнение измерений в вероятностном алгоритме может быть представлено в виде разностных матрично-векторных уравнений
Xk+1=ФXk+ГWk
Zk+1=HXk+ν k+1, где Х – вектор состояния Ф – фундаментальная матрица (математическая модель движения объекта) Г - матрица коэффициентов погрешностей измерений Н – матрица коэффициентов проекций градиентов навигационных параметров
ν - вектор шумов измерений W – вектор шумов системы (воздействие окружающей среды) Z – вектор значений измерений
Первое уравнение системы описывает динамику движения объекта. Второе уравнение системы описывает динамику погрешностей измерений.
Вопрос№28
Характер погрешности измеренного параметра по различным системам различен. Повысить точность и надёжность ОМС можно за счёт совместного использования нескольких измерительных систем:
- автономная навигационная система - спутниковая сетевая РНС
yизм(t)=yист(t)+ Δ y(t)aнс+ξ (t)aнс - автономная система
yизм(t)=yист(t)+ Δ y(t)срнс+ξ (t)срнс - СРНС
Погрешности СРНС имеют хорошую долговременную стабильность параметра на воздействие широкополосных помех.
Погрешности АНС обладают хорошей кратковременной стабильностью.
В случае, если годограф передаточной функции проходит через точку [-1; j0], то система находится на грани устойчивости (консервативная система)
Вопрос№22
Данные системы характеризуются тем, что управляющий алгоритм автоматически, целенаправленно изменяется для достижения успешного или в каком-либо смысле оптимального управления.
Все адаптивные САУ делятся на 3 вида:
Самонастраивающаяся система – адаптация в данной системе осуществляется путем изменения параметров управляющих воздействий
Самоорганизующаяся система – система, в которой адаптация осуществляется путем изменения не только параметров u(t), но и структура управляющего устройства. (т.е. меняется алгоритм обработки результатов измерений).
Самообучающаяся САУ – это САУ, в которой оптимальный режим работы объекта управления определяется при помощи управляющего устройства, алгоритм которого автоматически целенаправленно совершенствуется в процессе обучения, путем автопоиска. При этом при выборе решения, система автоматически запоминает все предыдущие состояния.
Вопрос№25
Особенности решения навигационной задачи с использованием вероятностных алгоритмов обработки результатов измерений.
Основное содержание заключается в определении координат и скоростей объекта являющихся основой их вектора состояния. X=[φ; λ; Δ B]
- географическая система координат низкоскоростных объектов. x=[x, y, z, x, ỳ, z, Δ B, Δ B] - для высокоскоростных объектов
Для нахождения данных величин, используют алгоритмы, которые отличаются ходом вычислительного процесса. На практике используются итерационные алгоритмы. В основу метода статистического оценивания могут быть положены следующие критерии качества оптимизации:
1.минимум дисперсии ошибок оценки вектора состояния
2.минимум суммы модуля невязок
3.максимум функций правдоподобия
4.максимум плотности апостериорной вероятности
Уравнение измерений в вероятностном алгоритме может быть представлено в виде разностных матрично-векторных уравнений
Xk+1=ФXk+ГWk
Zk+1=HXk+ν k+1, где Х – вектор состояния Ф – фундаментальная матрица (математическая модель движения объекта) Г - матрица коэффициентов погрешностей измерений Н – матрица коэффициентов проекций градиентов навигационных параметров
ν - вектор шумов измерений W – вектор шумов системы (воздействие окружающей среды) Z – вектор значений измерений
Первое уравнение системы описывает динамику движения объекта. Второе уравнение системы описывает динамику погрешностей измерений.
Вопрос№28
Характер погрешности измеренного параметра по различным системам различен. Повысить точность и надёжность ОМС можно за счёт совместного использования нескольких измерительных систем:
- автономная навигационная система - спутниковая сетевая РНС
yизм(t)=yист(t)+ Δ y(t)aнс+ξ (t)aнс - автономная система
yизм(t)=yист(t)+ Δ y(t)срнс+ξ (t)срнс - СРНС
Погрешности СРНС имеют хорошую долговременную стабильность параметра на воздействие широкополосных помех.
Погрешности АНС обладают хорошей кратковременной стабильностью.
 В связи с тем, что различные навигационные системы имеют различные частотные характеристики погрешностей то имеется возможность их разделения и выделения, т.е. фильтрация. Рассмотрим в качестве примера схему компенсаций погрешностей измерений с помощью фильтра Калмана:
На выходе фильтра в результате фильтрации получаем ψ ист+δ /АНС- δ /АНС= ψ ист - не верно. Ψ ист+ δ АНСδ ^АНС - ψ ист + δ ф
В результате использования фильтра Калмана, результирующая погрешность алгоритма компенсации определяется только погрешностью работы фильтра Калмана. Для повышения точности работы алгоритма компенсации, необходимо повышать точность математической модели погрешности измерений.
Особенности решения навигационной задачи с использованием вероятностных алгоритмов обработки результатов измерений.
Основное содержание заключается в определении координат и скоростей объекта являющихся основой их векторосостояния.
В связи с тем, что различные навигационные системы имеют различные частотные характеристики погрешностей то имеется возможность их разделения и выделения, т.е. фильтрация. Рассмотрим в качестве примера схему компенсаций погрешностей измерений с помощью фильтра Калмана:
На выходе фильтра в результате фильтрации получаем ψ ист+δ /АНС- δ /АНС= ψ ист - не верно. Ψ ист+ δ АНСδ ^АНС - ψ ист + δ ф
В результате использования фильтра Калмана, результирующая погрешность алгоритма компенсации определяется только погрешностью работы фильтра Калмана. Для повышения точности работы алгоритма компенсации, необходимо повышать точность математической модели погрешности измерений.
Особенности решения навигационной задачи с использованием вероятностных алгоритмов обработки результатов измерений.
Основное содержание заключается в определении координат и скоростей объекта являющихся основой их векторосостояния.
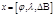 - географическая система координат низкоскоростных объектов.
- географическая система координат низкоскоростных объектов.
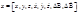 - для высокоскоростных объектов
Для нахождения данных величин, используют алгоритмы, которые отличаются ходом вычислительного процесса. На практике используются итерационные алгоритмы. В основу метода статистического оценивания могут быть положены следующие критерии качества оптимизации: 1.минимум дисперсии ошибок оценки вектора состояния. 2.минимум суммы модуля невязок. 3.максимум функций правдоподобия. 4.максимум плотности апостериорной вероятности.
Уравнение измерений в вероятностном алгоритме может быть представлено в виде разностных матрично-векторных уравнений
- для высокоскоростных объектов
Для нахождения данных величин, используют алгоритмы, которые отличаются ходом вычислительного процесса. На практике используются итерационные алгоритмы. В основу метода статистического оценивания могут быть положены следующие критерии качества оптимизации: 1.минимум дисперсии ошибок оценки вектора состояния. 2.минимум суммы модуля невязок. 3.максимум функций правдоподобия. 4.максимум плотности апостериорной вероятности.
Уравнение измерений в вероятностном алгоритме может быть представлено в виде разностных матрично-векторных уравнений
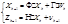 , где Х – вектор состояния; Ф – фундаментальная матрица (математическая модель движения объекта); Г - матрица коэффициентов погрешностей измерений; Н – матрица коэффициентов проекций градиентов навигационных параметров; V - вектор шумов измерений; W – вектор шумов системы (воздействие окружающей среды); Z – вектор значений измерений.
Первое уравнение системы описывает динамику движения объекта. Второе уравнение системы описывает динамику погрешностей измерений.
Окончательно, алгоритм фильтрации методом Калмана имеет вид:
, где Х – вектор состояния; Ф – фундаментальная матрица (математическая модель движения объекта); Г - матрица коэффициентов погрешностей измерений; Н – матрица коэффициентов проекций градиентов навигационных параметров; V - вектор шумов измерений; W – вектор шумов системы (воздействие окружающей среды); Z – вектор значений измерений.
Первое уравнение системы описывает динамику движения объекта. Второе уравнение системы описывает динамику погрешностей измерений.
Окончательно, алгоритм фильтрации методом Калмана имеет вид:
 , где КК- коэффициент усиления фильтра;
РК - ковариационная матрица погрешностей оценки навигационного сеанса.
Собственное значение матрицы Р определяют полуоси эллипса погрешностей. А собственные вектора матрицы определяют направление этих полуосей. Таким образом с использованием фильтра Калмана имеется возможность на каждый конкретный момент времени определять эллипс погрешности навигационного сеанса. Имеется возможность автоматически подстраивать работу фильтра через его коэффициент усиления к текущим условиям плавания. Это дает возможность создания автоматических адоптивных систем управлением движения судна.
, где КК- коэффициент усиления фильтра;
РК - ковариационная матрица погрешностей оценки навигационного сеанса.
Собственное значение матрицы Р определяют полуоси эллипса погрешностей. А собственные вектора матрицы определяют направление этих полуосей. Таким образом с использованием фильтра Калмана имеется возможность на каждый конкретный момент времени определять эллипс погрешности навигационного сеанса. Имеется возможность автоматически подстраивать работу фильтра через его коэффициент усиления к текущим условиям плавания. Это дает возможность создания автоматических адоптивных систем управлением движения судна.
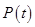 2.среднее время безотказной работы
2.среднее время безотказной работы 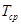 3.интенсивность отказов
3.интенсивность отказов 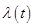 4.эксплуатационные коэффициенты:
- коэффициент готовности
4.эксплуатационные коэффициенты:
- коэффициент готовности 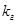 .
- коэффициент вынужденного простоя
.
- коэффициент вынужденного простоя 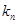 .
- коэффициент расхода элементов
.
- коэффициент расхода элементов 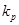 .
5.Вероятность безопасной работы системы – случайная функция времени, в течение которого не возникает ни одного отказа.
6. Вероятность отказа – противоположная функция появляемости событий.
Функциональная надежность Навигационной аппаратуры определяется комплексом мер:
Одобренный проект Регистром на установку данного изделия на судно.
В проект включается: расположение антенн для решения вопроса о электромагнитной совместимости, расположение основного прибора для удобства использования, монтаж оборудования (крепление устройства, прокладка кабелей, прохождение водонепроницаемых переборок, подключение к источнику питания).
.
5.Вероятность безопасной работы системы – случайная функция времени, в течение которого не возникает ни одного отказа.
6. Вероятность отказа – противоположная функция появляемости событий.
Функциональная надежность Навигационной аппаратуры определяется комплексом мер:
Одобренный проект Регистром на установку данного изделия на судно.
В проект включается: расположение антенн для решения вопроса о электромагнитной совместимости, расположение основного прибора для удобства использования, монтаж оборудования (крепление устройства, прокладка кабелей, прохождение водонепроницаемых переборок, подключение к источнику питания).
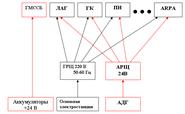 По требованиям SOLAS аккумуляторы должны обеспечивать работу оборудования ГМССБ в течении 6 часов.
Квалифицированная эксплуатация бортовой аппаратуры.
По требованиям SOLAS аккумуляторы должны обеспечивать работу оборудования ГМССБ в течении 6 часов.
Квалифицированная эксплуатация бортовой аппаратуры.
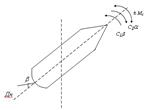
 , где I – момент инерции создаваемый движителем, w - угловая скорость, L - сумма моментов сил, действующих на корпус судна в результате перекладки пера руля и внешних факторов. С другой стороны, L=c1b-c2a±Mc, здесь c1, c2 - гидродинамические коэффициенты, зависящие от самой конструкции корпуса судна, шага винта, обрастания и т.д., и представляют собой сложные эмпирические зависимости, которые рассчитываются при испытаниях головной модели в серии. b - угол перекладки пера руля; a - скорость изменения положения ДП судна относительно вертикальной оси; Mc - суммарный момент сил внешних факторов, действующих на судно.
, где I – момент инерции создаваемый движителем, w - угловая скорость, L - сумма моментов сил, действующих на корпус судна в результате перекладки пера руля и внешних факторов. С другой стороны, L=c1b-c2a±Mc, здесь c1, c2 - гидродинамические коэффициенты, зависящие от самой конструкции корпуса судна, шага винта, обрастания и т.д., и представляют собой сложные эмпирические зависимости, которые рассчитываются при испытаниях головной модели в серии. b - угол перекладки пера руля; a - скорость изменения положения ДП судна относительно вертикальной оси; Mc - суммарный момент сил внешних факторов, действующих на судно.
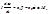 Учитывая, что w=da/dt, получаем
Учитывая, что w=da/dt, получаем 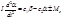
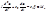 Используем преобразование Лапласа и разделим все уравнения на c2, в результате получим:
Используем преобразование Лапласа и разделим все уравнения на c2, в результате получим:
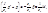 Обозначим:
I/c2=T- постоянная времени судна, описывает инерционные характеристики судна.
c1/c2=K - коэффициент усиления по управлению. Описывает эффективность воздействия пера руля.
1/c2=`K- коэффициент усиления по внешнему воздействию.
Подставим в уравнение, получим
(Tp2+p)a-Kb± =`K Mc - основное уравнение для получения передаточной функции.
1.Рассмотрим случай движения судна при b¹ 0 и Mc=0 (движение судна при нормальных условиях).
Обозначим:
I/c2=T- постоянная времени судна, описывает инерционные характеристики судна.
c1/c2=K - коэффициент усиления по управлению. Описывает эффективность воздействия пера руля.
1/c2=`K- коэффициент усиления по внешнему воздействию.
Подставим в уравнение, получим
(Tp2+p)a-Kb± =`K Mc - основное уравнение для получения передаточной функции.
1.Рассмотрим случай движения судна при b¹ 0 и Mc=0 (движение судна при нормальных условиях). 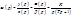 - передаточная функция по управляющему воздействию.
2.Рассмотрим движение судна приb=0 и Mc¹ 0 (прямолинейное движение судна при воздействии внешних факторов)
- передаточная функция по управляющему воздействию.
2.Рассмотрим движение судна приb=0 и Mc¹ 0 (прямолинейное движение судна при воздействии внешних факторов)
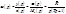 - передаточная функция по внешнему фактору.
- передаточная функция по внешнему фактору.

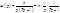 wS=w(p1)+ w(p2), где
wS=w(p1)+ w(p2), где
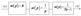 w(p)=k - усилительное звено
w(p)=1/p - интегрирующее звено
w(p)=1/(Tp+1) - апериодическое звено
w(p)=k - усилительное звено
w(p)=1/p - интегрирующее звено
w(p)=1/(Tp+1) - апериодическое звено
 Различают несколько режимов работы современного авторулевого:
1.Ручное управление. 2.Полуавтоматическое (следящий режим). 3.Автоматическое управление.
Различают несколько режимов работы современного авторулевого:
1.Ручное управление. 2.Полуавтоматическое (следящий режим). 3.Автоматическое управление.
 1. Рассмотрим ручное управление
ИД – исполнительный двигатель
РМ – рулевая машина
Алгебра передаточных функций
1. Рассмотрим ручное управление
ИД – исполнительный двигатель
РМ – рулевая машина
Алгебра передаточных функций
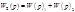
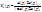
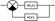 Знак в знаменателе определяется типом обратной связи. При положительной - «-», а при отрицательной – «+».
Знак в знаменателе определяется типом обратной связи. При положительной - «-», а при отрицательной – «+».
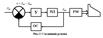
 Быстродействие данного режима определяется коэффициентом обратной связи.
Быстродействие данного режима определяется коэффициентом обратной связи.
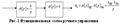
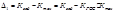
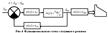
 Коэффициент обратной связи (КОС) влияет на быстродействие системы в целом.
Коэффициент обратной связи (КОС) влияет на быстродействие системы в целом.
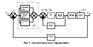 Качество регулирования определяется блоком коррекции:
1.Интегратор учитывает (компенсирует) снос судна из-за действия ветра и течения. 2.Тахогенератор влияет на перерегулирование. 3.Сельсин-трансформатор вырабатывает сигнал, пропорциональный углу поворота штурвала.
Таким образом качество переходного процесса определяется КОС, интегратором и тахогенератором.
На выходе блока коррекции сигнал представлен следующей формулой:
Качество регулирования определяется блоком коррекции:
1.Интегратор учитывает (компенсирует) снос судна из-за действия ветра и течения. 2.Тахогенератор влияет на перерегулирование. 3.Сельсин-трансформатор вырабатывает сигнал, пропорциональный углу поворота штурвала.
Таким образом качество переходного процесса определяется КОС, интегратором и тахогенератором.
На выходе блока коррекции сигнал представлен следующей формулой:
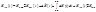 Для подстройки авторулевого к текущим условиям плавания необходимо использовать 3 коэффициента:
Для подстройки авторулевого к текущим условиям плавания необходимо использовать 3 коэффициента: