💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Определение ЭДС методом компенсации

Сущность метода компенсации ЭДС состоит в следующем. Рассмотрим принципиальную электрическую схему, представленную на рис. 32.1. Источник тока с ЭДС E подключается к реохорду AB, а исследуемый элемент с ЭДС E_x присоединяют к началу реохорда A и через чувствительный гальванометр Г к подвижному контакту реохорда С. При этом необходимо выполнить два условия: 1) ЭДС элемента E должна быть больше ЭДС элемента E_х, 2) к точке А реохорда элементы подключаются одинаковыми полюсами.

Так как Е > Е_x, то на реохорде АВ всегда будет такая точка, разность потенциалов между которой и точкой А будет равна электродвижущей силе исследуемого элемента. Перемещая контакт С вдоль реохорда, ищут такое его положение, при котором в контуре AFГС с элементом Е_x тока не будет. При этом происходит компенсация падения напряжения на участке АС реохорда и подключенной к этому участку электродвижущей силы Е_x.

Отсутствие тока в гальванометре становится возможным только при соединении источников ЭДС в схеме одноименными полюсами. В этом случае ток I₂, который ответвился бы в контур AFГС при отсутствии в нем элемента Е_x, и ток I₁, индуцированный элементом Е_x, текут в противоположных направлениях. Ток I₂ – от “плюса” (точка А) через точки F и Г к “минусу” (точка С), т.е. против часовой стрелки. Ток I₁ – от “плюса” к “минусу” элемента Е_x, т.е. по часовой стрелке). При компенсации токи I₁ и I₂ становятся равными по величине, и суммарный ток через гальванометр не идет.

При условии, что ЭДС Е_x скомпенсирована, ток I в контуре AODB не разветвляется и равен:

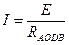, (32.1)

где R_AODB – полное сопротивление контура AODB. Обозначим r_x сопротивление участка цепи между точками А и С. Тогда разность потенциалов V_A - V_C между точками А и С:

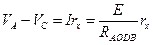. (32.2)

Следовательно, электродвижущая сила Е_x исследуемого элемента равна:

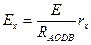. (32.3)

Если заменить исследуемый элемент нормальным элементом Вестона, электродвижущая сила Е_n которого известна, и вновь добиться отсутствия тока в контуре AFГС, можно получить:

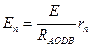. (32.4)

Разделив выражение (32.3) на выражение (32.4), имеем:

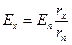. (32.5)

Таким образом, сравнение электродвижущих сил двух элементов может быть практически сведено к сравнению двух сопротивлений, использованных при компенсационных измерениях.

Метод компенсации для определения ЭДС обладает рядом важных преимуществ. Во-первых, сила тока через элементы, ЭДС которых сравниваются между собой, близка к нулю. Точность измерений ограничивается ценой деления гальванометра, которая соответствует 10^-6 – 10^-7 А у различных типов стрелочных гальванометров. Поэтому падения напряжения внутри элемента, снижающего значение измеренной на полюсах элемента разности потенциалов, практически нет. Не существенным является и падение напряжения в проводах, соединяющих элемент с измерительной схемой. Во-вторых, при компенсационном методе гальванометр работает как нулевой прибор и градуировка его шкалы в результат измерений не входит. Наконец, величина ЭДС вспомогательной батареи Е также не входит в окончательный результат. Необходимо лишь, чтобы величина ее ЭДС во время измерений была постоянной. Рабочая схема для измерения ЭДС источника напряжения методом компенсации показана на рис. 32.2.

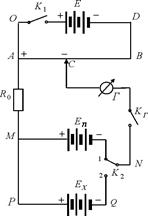
Она состоит из трех контуров, в каждый из которых включен источник напряжения. Контур AODB состоит из источника напряжения E, ключа K 1 и струны реохорда AB (длинной проволоки с большим удельным сопротивлением 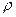). При замыкании ключа K 1 элемент Е подключается к реохорду. В контуре AMNC включено большое сопротивление R 0 (порядка 105 Ом), нормальный элемент E n, ЭДС которого известна с большой степенью точности, двойной ключ K 2 и чувствительный нуль-гальванометр Г.

Рис.32.2

В контур APQNC включены сопротивление R ₀, источник E_x, величину ЭДС которого следует измерить, ключ K ₂ и гальванометр Г. Контакт C может свободно перемещаться по струне реохорда.

Ключ K ₂ при замыкании может находиться либо в положении 1, тогда в цепь включается элемент E _n , либо в положении 2, тогда в цепь включается исследуемый источник E _x.

Большое сопротивление R ₀ необходимо включать в схему по следующей причине. Если в цепь включается нормальный элемент Вестона, то этот источник напряжения сохраняет неизменной свою ЭДС с точностью до шестого знака (при постоянной температуре) только в том случае, когда через источник течет ток, не превышающий 10^-4 А. В противном случае нормальный элемент поляризуется и его ЭДС уменьшается. Кроме того, большое сопротивление R ₀ служит для защиты чувствительного гальванометра Г от слишком больших токов при включении его в момент сильной раскомпенсации схемы.

Рассмотрим процесс измерения ЭДС по схеме рис. 32.2. Ключ K ₂ включен в положение 1. При этом в схему включается нормальный элемент. Перемещая контакт C вдоль струны реохорда, добиваются отсутствия тока в гальванометре. Гальванометр имеет свой ключ К _г . Включать этот ключ надо на очень непродолжительное время, чтобы убедиться, что компенсация в схеме еще не достигнута. При достижении компенсации ЭДС нормального элемента будет в точности равна падению напряжения на участке струны реохорда AC, сопротивление которого мы обозначим r _n.

Переключим теперь ключ K ₂ в положение 2. Этим самым мы включаем в цепь измеряемый источник напряжения E _x. Передвигая контакт C на реохорде, необходимо добиться компенсации ЭДС E _x на новом сопротивлении r _x.

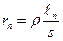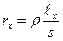Если струна реохорда однородна, то и , где 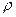– удельное сопротивление струны реохорда, а S – площадь его поперечного сечения. В этом случае равенство (32.5) приобретает вид:

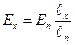(32.6)

Таким образом, измерение ЭДС сводится к измерению длин 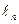и 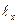участков струны реохорда, на которых выполняется компенсация.