Основы теории статистического контроля

Выборочный контроль, построенный на научной основе, т.е. исходящий из теории вероятностей и математической статистики, называют статистическим контролем. Предпринимателя и менеджера выборочный контроль может интересовать не только в связи с качеством продукции, но и в связи, например, с контролем экологической обстановки, поскольку зафиксированные государственными органами экологические нарушения влекут штрафы и иные " неприятные" последствия. Или в связи с выборочным контролем документации.

Обсудим основные подходы статистического контроля.

При статистическом контроле решение о генеральной совокупности - об экологической обстановке в данном регионе или о партии продукции - принимается по выборке, состоящей из некоторого количества единиц (единиц экологического контроля или единиц продукции). Следовательно, выборка должна представлять партию, т.е. быть репрезентативной (представительной). Как эти слова понимать, как проверить репрезентативность? Ответ может быть дан лишь в терминах вероятностных моделей выборки.

Наиболее распространенными являются две вероятностные модели - биномиальная и гипергеометрическая. В первой из них предполагается, что результаты контроля 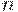единиц можно рассматривать как совокупность n независимых одинаково распределенных случайных величин 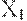, , 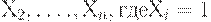если 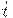ое измерение показывает, что имеется нарушение, т.е. превышено ПДК (предельная норма концентрации) или 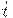ое изделие дефектно, и , если это не так. Тогда число 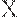превышений ПДК (при другой интерпретации - дефектных единиц продукции в партии) равно

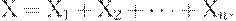
(1)

Известно, что распределение 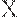имеет вид

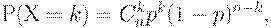
(2)

где 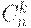- число сочетаний из 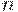элементов по 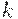, а 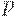-уровень дефектности (в другой предметной области - в экологии - доля превышений ПДК в генеральной совокупности), т.е. 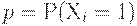. Формула (2) задает так называемое биномиальное распределение.

Из формулы (1) и Центральной Предельной Теоремы теории вероятностей вытекает, что при увеличении объема выборки n распределение 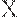сближается с нормальным распределением.

Вторая модель - гипергеометрическая - соответствует случайному отбору единиц в выборку. Пусть среди 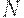единиц, составляющих генеральную совокупность, имеется 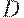дефектных. Случайность отбора означает, что каждая единица имеет одинаковые шансы попасть в выборку. Более того, ни одна пара единиц не имеет преимущества перед любой другой парой при отборе в выборку. То же самое - для троек, четверок и т.д. Итак, каждое из сочетаний по 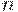единиц из 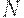имеет одинаковую вероятность быть отобранным в качестве выборки, равную, очевидно, .

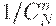Отбор случайной выборки согласно описанным правилам организуют при проведении различных лотерей. Пусть 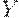-число дефектных единиц в такой выборке. Известно, что тогда 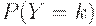- гипергеометрическое распределение, т.е.

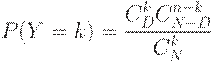
Замечательный математический результат состоит в том, что биномиальная и гипергеометрическая модели весьма близки, когда объем генеральной совокупности (партии) по крайней мере в 10 раз превышает объем выборки. Таким образом, можно констатировать, что

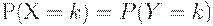
(3)

с достаточной для практики точностью, если объем выборки мал по сравнению с объемом партии. При этом в качестве p в формуле (2) берут .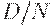

Близость результатов, получаемых с помощью биномиальной и гипергеометрической моделей, весьма важна с методологической точки зрения. Дело в том, что эти модели исходят из принципиально различных методологических предпосылок. В биномиальной модели случайность присуща каждой единице - она с какой-то вероятностью дефектна, а с какой-то - годна. В то же время в гипергеометрической модели качество определенной единицы детерминировано, задано, а случайность проявляется лишь в отборе, вносится инженером, экологом или экономистом при составлении выборки.

В науках о человеке противоречие между двумя рассматриваемыми моделями выборки еще более выражено. Биномиальная модель предполагает, что поведение человека, в частности, выбор им определенного варианта при ответе на вопрос, определяется с участием случайных причин. Например, человек может случайно сказать " да", случайно - " нет". Некоторые философы отрицают присущую поведению человека случайность. Они верят в причинность и считают поведение конкретного человека практически полностью определенным (детерминированным) его взглядами, жизненным опытом, окружающей средой. Поэтому они принимают гипергеометрическую модель и считают, что случайность отличия ответов в выборке от ответов во всей генеральной совокупности определяется всецело случайностью, вносимой при отборе единиц наблюдения в выборку.

Соотношение (3) показывают, что во многих случаях нет необходимости выбирать одну из моделей, поскольку обе дают близкие численные результаты. Отличия проявляются при обсуждении вопроса о том, какую выборку считать представительной. Является ли таковой выборка, составленная из 20 изделий, лежащих сверху в первом вскрытом ящике? В биномиальной модели вполне допустим ответ " да", в гипергеометрической - только " нет".

Биномиальная модель легче для теоретического изучения, поэтому будем её рассматривать в дальнейшем. Однако при реальном контроле лучше формировать выборку, исходя из гипергеометрической модели. Это делают, выбирая номера изделий (для включения в выборку) с помощью датчиков псевдослучайных чисел на ЭВМ или с помощью таблиц псевдослучайных чисел. Алгоритмы формирования выборки встраивают в современные программные продукты по статистическому контролю.

Планы статистического контроля и правила принятия решений. Под планом статистического контроля понимают алгоритм, т.е. правила действий при контроле качества. На " входе" при этом - генеральная совокупность (партия продукции), а на " выходе" - одно из двух решений: " принять партию" либо " забраковать партию". Рассмотрим несколько примеров.

Одноступенчатые планы контроля 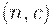: отобрать выборку объема n; если число дефектных единиц в выборке 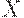не превосходит 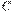, то партию принять, в противном случае забраковать. Число с называется " приемочным числом".

Частные случаи: план 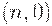-партию принять тогда и только тогда, когда все единицы в выборке являются годными; план 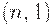- партия принимается, если в выборке все единицы являются годными или ровно одно - дефектное, во всех остальных случаях партия бракуется.

Двухступенчатый план контроля 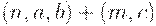: отобрать первую выборку объема n; если число дефектных единиц в первой выборке 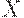не превосходит 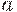, то партию принять; если число дефектных единиц в первой выборке 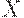больше или равно 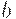, то партию забраковать; во всех остальных случаях, т.е. когда 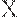больше 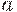, но меньше 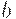, следует взять вторую выборку объема 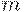; если число дефектных единиц во второй выборке 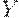не превосходит 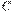, то партию принять, в противном случае забраковать.

Рассмотрим в качестве примера план 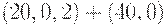. Сначала берется первая выборка объема 20. Если все единицы в ней - годные, то партия принимается. Если две или больше - дефектные, партия бракуется. А если только одно - дефектное? В реальной ситуации в таких случаях начинаются споры между представителями предприятия и экологического контроля, или поставщика и потребителя. Говорят, например, что дефектная единица случайно попала в партию, что ее подсунули конкуренты или что при контроле случайно сделан неправильный вывод. Поэтому, чтобы споры пресечь, берут вторую выборку объема 40 (вдвое большего, чем в первый раз). Если все единицы во второй выборке - годные, то партию принимают, в противном случае - бракуют.

В реальной нормативно-технической документации - договорах на поставку, технических регламентах, стандартах, технических условиях, инструкциях по экологическому контролю и т.д. - не всегда четко сформулированы планы статистического контроля и правила принятия решений. Например, при описании двухступенчатого плана контроля вместо задания приемочного числа с может стоять загадочная фраза " результат контроля второй выборки считается окончательным". Остается гадать, как принимать решение по второй выборке. Менеджер, администратор (государственный служащий), инженер, эколог или экономист, занимающийся вопросами экологического контроля или контроля качества, должен первым делом добиваться кристальной ясности в формулировках правил принятия решений, иначе ошибочные и необоснованные решения, а потому и убытки неизбежны.

Оперативная характеристика плана статистического контроля. Каковы свойства плана статистического контроля? Они, как правило, определяются с помощью функции 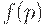, связывающей вероятность 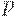дефектности единицы контроля с вероятностью 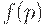приемки партии, положительной оценки экологической обстановки или заключения о правильности ведения бухгалтерской документации по результатам контроля. При этом вероятность p того, что конкретная единица дефектна, называется входным уровнем дефектности, а указанная функция называется оперативной характеристикой плана контроля. Если дефектные единицы отсутствуют, , то партия всегда принимается, т.е. 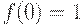. Если все единицы дефектные, , то партия наверняка бракуется, 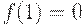. Между этими крайними значениями 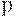функция 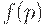монотонно убывает. При изучении свойств плана входной уровень дефектности 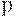- свободный параметр, он может принимать любые значения между 0 и 1.

Вычислим оперативную характеристику плана 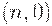. Поскольку партия принимается тогда и только тогда, когда все единицы являются годными, а вероятность того, что конкретная единица - годная, равна 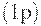, то оперативная характеристика имеет вид

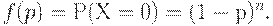
(4)

Для плана 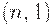оперативная характеристика, как легко видеть, такова:

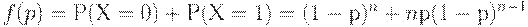
(5)

Оперативные характеристики для конкретных планов статистического контроля не всегда имеют такой простой вид, как в случае формул (4) и (5). Рассмотрим в качестве примера план (20, 0, 2) + (40, 0). Сначала найдем вероятность того, что партия будет принята по результатам контроля первой партии. Согласно формуле (4) имеем:

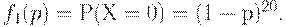
Вероятность того, что понадобится контроль второй выборки, равна

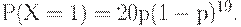
При этом вероятность того, что по результатам её контроля партия будет принята, равна

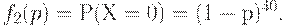
Следовательно, вероятность того, что партия будет принята со второй попытки, т.е. что при контроле первой выборки обнаружится ровно одна дефектная единица, а затем при контроле второй - ни одной, равна

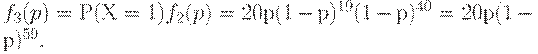
Следовательно, вероятность принятия партии с первой или со второй попытки равна

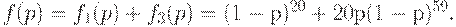
При практическом применении методов статистического приемочного контроля для нахождения оперативных характеристик планов контроля вместо формул, имеющих обозримый вид лишь для отдельных видов планов, применяют численные компьютерные алгоритмы или заранее составленные таблицы.

Риск поставщика и риск потребителя, приемочный и браковочный уровни дефектности. С оперативной характеристикой связаны важные понятия приемочного и браковочного уровней дефектности, а также понятия " риск поставщика " и " риск потребителя". Чтобы ввести эти понятия, на оперативной характеристике выделяют две характерные точки, делящие входные уровни дефектности на три зоны (област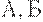и) - и 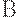. В зоне почти всегда все хорошо, а именно - почти всегда экологическая обстановка признается благополучной, почти все партии принимаются. В зоне 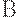, наоборот, почти всегда все плохо, а именно - почти всегда экологический контроль констатирует экологические нарушения, почти все партии бракуются. Зона 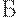- буферная, переходная, промежуточная, в ней как вероятность приемки, так и вероятность браковки заметно отличаются от 0 и 1. Для задания границ между зонами выбирают два малых числа- риск поставщика (производителя, предприятия) 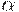и риск потребителя (заказчика, системы экологического контроля) 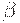, при этом границы между зонами задают два уровня дефектности - приемочный 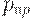и браковочный 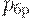, определяемые из уравнений

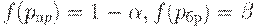
(6)

Таким образом, если входной уровень дефектности не превосходит 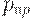, то вероятность забракования партии мала, т.е. не превосходит 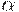. Приемочный уровень дефектности выделяет зону значений входного уровня дефектности, в которой нарушения экологической безопасности почти всегда не отмечаются, партии почти всегда принимаются, т.е. соблюдаются интересы проверяемого предприятия (в экологии), поставщика (при контроле качества). Это - зона комфортности для поставщика. Если он обеспечивает работу (входной уровень дефектности) в этой зоне, то его практически никогда никто не потревожит.

Если же входной уровень дефектности больше браковочного уровня дефектности 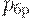, то нарушения почти наверняка фиксируются, партия почти всегда бракуется, т.е. экологи узнают о нарушениях, потребитель оказывается защищен от попадания к нему партий со столь высоким уровнем брака. Поэтому можно сказать, что в зоне 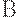соблюдаются интересы потребителей - брак к ним не попадает.

При выборе плана контроля часто начинают с выбора приемочного и браковочного уровней дефектности. При этом выбор конкретного значения приемочного уровня дефектности отражает интересы поставщика, а выбор конкретного значения браковочного уровня дефектности - интересы потребителя. Можно доказать (см. ниже), что для любых положительных чисел 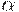и 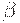и любых входных уровней дефектност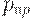и и 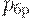, причем 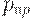меньше 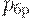, найдется план контроля 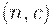такой, что его оперативная характеристика 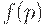удовлетворяет неравенствам

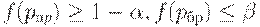
При практических расчетах обычно принимают 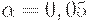(т.е. 5%) и 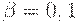(т.е. 10%).

В качестве примера вычислим приемочный и браковочный уровни дефектности для плана 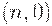. Из формул (4) и (6) вытекает, что

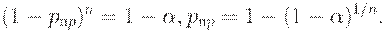
Поскольку риск поставщика 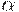мал, то из известного соотношения математического анализа

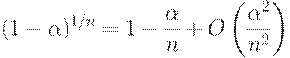
вытекает приближенная формула

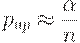
Для браковочного уровня дефектности имеем

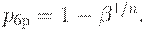
При практическом применении методов статистического приемочного контроля аналитическими формулами, имеющими обозримый вид лишь для отдельных видов планов, не пользуются. Для нахождения приемочных и браковочных уровней дефектности планов контроля вместо них применяют численные компьютерные алгоритмы или заранее составленные таблицы. Такие таблицы имеются в нормативно-технической документации или научно-технических публикациях.

Предел среднего выходного уровня дефектности. Обсудим судьбу забракованной партии продукции. В зависимости от ситуации эта судьба может быть разной. Партия может быть утилизирована. Например, забракованная партия гвоздей может быть направлена на переплавку. У партии может быть понижена сортность, и она может быть продана по более низкой цене (при этом результаты выборочного контроля будут использованы не только для констатации того, что не выдержан заданный уровень качества, но и для оценки реального уровня качества). Наконец, партия продукции может быть подвергнута сплошному контролю (для этого обычно привлекают инженеров из всех заводских служб). При сплошном контроле все дефектные изделия обнаруживаются и либо исправляются на месте, либо извлекаются из партии. В результате в партии остаются только годные изделия. Такая процедура называется " контроль с разбраковкой".

При среднем входном уровне дефектности 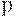и применении контроля с разбраковкой с вероятностью 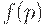партия принимается (и уровень дефектности в ней по -прежнему равен 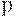) и с вероятностью 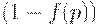бракуется и подвергается сплошному контролю, в результате чего к потребителю поступают только годные изделия. Следовательно, по формуле полной вероятности средний выходной уровень дефектности равен

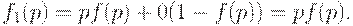
Средний выходной уровень дефектности 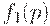равен 0 при и , положителен на интервале (0; 1), а потому достигает на нем максимума, который в теории статистического контроля называется пределом среднего выходного уровня дефектности (сокращенно ПСВУД):

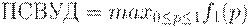
Пример. Рассмотрим план 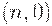. Для него 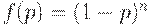и 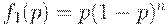. Чтобы найти ПСВУД, надо приравнять 0 производную среднего выходного уровня дефектности по среднему входному уровню дефектности:

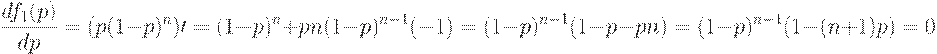
В полученном уравнении корень соответствует минимуму, а не максимуму. Поскольку непрерывная функция на замкнутом отрезке достигает максимума, то максимум достигается при

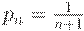
Следовательно,

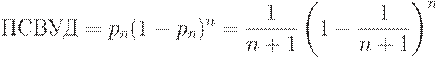
(7)

По выражению (7) могут быть проведены конкретные расчеты. Однако оно довольно громоздко. Его можно упростить, используя один замечательный предел из курса математического анализа, а именно:

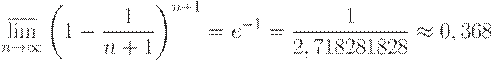
(8)

Сравнивая соотношения (7) и (8), видим, что

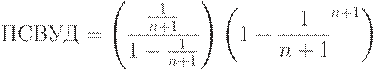
Первая скобка равна 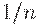, а вторая согласно соотношению (8) приближается к 0, 368 при росте объема выборки. Поэтому получаем простую асимптотическую формулу

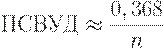
Для более сложных планов ПСВУД рассчитывают с помощью более или менее сложных компьютерных программ.

При проведенном выше рассмотрении основ статистического контроля расчетные формулы удалось получить лишь для простейших планов, в основном для планов вида 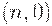. Если ослабить требования и рассчитывать не на точные формулы, а на асимптотические, при 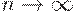, то можно справиться и с одноступенчатыми планами вида .

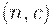Асимптотическая теория одноступенчатых планов. Пусть 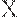- число дефектных единиц продукции в выборке объема 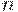. Как уже отмечалось, распределение 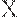является биномиальным и имеет вид

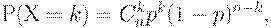
где 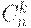- число сочетаний из 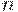элементов по 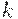, а 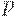- входной уровень дефектности.

Пусть используется одноступенчатый план контроля 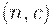. Тогда оперативная характеристика этого плана имеет вид

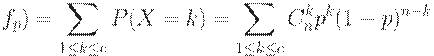
Пусть 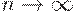Тогда по Закону Больших Чисел теории вероятностей (по теореме Бернулли)

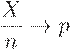
(сходимость по вероятности). Значит, если 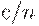окажется заметно больше входного уровня дефектности 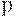, то партии будут почти всегда приниматься, а если 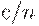окажется заметно меньше входного уровня дефектности 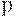, то партии будут почти всегда отклоняться. Ситуация будет нетривиальной только там, где величины 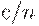и 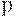близки друг к другу.

Хотя оперативная характеристика рассчитывается с помощью сумм биномиальных вероятностей, анализировать эти суммы затруднительно. Поэтому целесообразно найти для нее приближение с помощью теоремы Муавра-Лапласа. Имеем цепочку тождественных преобразований:

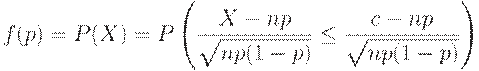
Справа стоит именно то выражение, которое участвует в теореме Муавра-Лапласа. Воспользовавшись равномерной сходимостью в этой теореме, можно записать, что

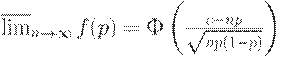
где 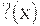- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.

Последняя формула позволяет указать асимптотические выражения для приемочного и браковочного уровней дефектности. Действительно, согласно определениям этих понятий

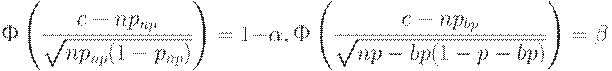
(9)

откуда с помощью элементарных преобразований получаем, что

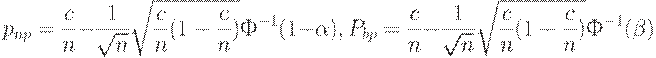
(10)

Так как величины 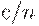и 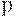близки друг к другу, то при переходе от формулы (9) к формуле (10) в подкоренных выражениях приемочный и браковочный уровни дефектности заменены на 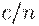(с точностью до бесконечно малых более высокого порядка).

Поскольку при практическом применении статистического приемочного контроля, как уже отмечалось, принимают 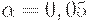, , 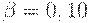то в предыдущие формулы следует подставить 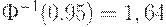и 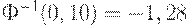Итак, итоговые формулы для приемочного и браковочного уровней дефектности имеют вид

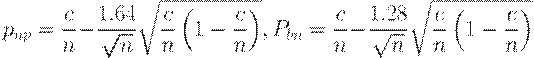
Перейдем к задаче синтеза. Пусть заданы приемочный и браковочный уровни дефектности. Требуется построить одноступенчатый план, имеющий эти характеристики. Из формул (9) следует, в частности, что

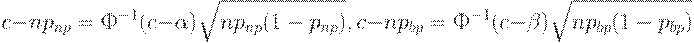
(11)

Вычитая из первого уравнения второе, получаем, что

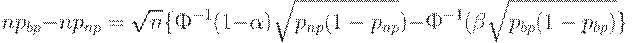
Следовательно, оценка необходимого объема выборки имеет вид

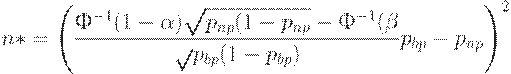
Для стандартных значений рисков 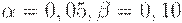имеем:

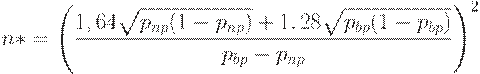
(12)

С помощью уравнений (11) нетрудно найти оценку 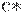приемочного числа, заменив неизвестный объем выборки на его оценку 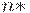. Будем использовать оценку

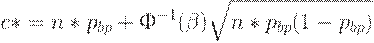
Для стандартного значения 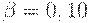имеем

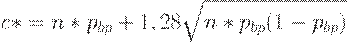
(13)

Итак, по формуле (12) можно рассчитать оценку объема выборки, затем по формуле (13) найти оценку приемочного числа. Необходимо отметить, что результаты расчетов по рассматриваемым асимптотическим формулам отнюдь не всегда дают целые числа, поэтому необходима корректировка полученных результатов.

Полученные формулы позволяют решить сформулированную выше задачу - по заданным приемочному и браковочному уровням дефектности подобрать такой одноступенчатый план контроля, что его оперативная характеристика 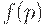удовлетворяет неравенствам

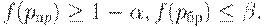
Поэтому при практической работе корректировка асимптотических результатов должна быть направлена на выполнение указанных неравенств.

Пример. Пусть 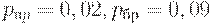. Тогда по формуле (12) оценка объема выборки равна

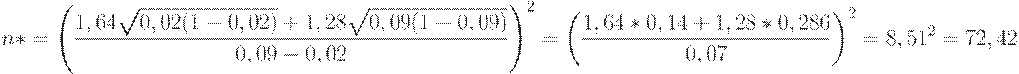
Полученное число не является натуральным, поэтому вполне естественно откорректировать объем выборки до ближайшего целого, т.е. до .

Оценку приемочного числа находим по формуле (13):

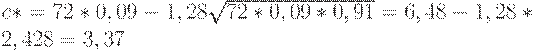
Полученное число не является целым, поэтому в качестве приемочного числа надо взять ближайшее целое, т.е. до 3.

Если объем выборки округлить до 73, то аналогично получим

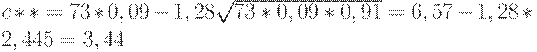
При округлении снова получаем 3.

С помощью первого из уравнений (11) можно построить оценку с* на основе приемочного уровня дефектности:

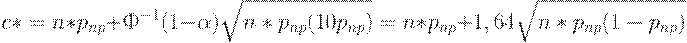
Подставив конкретные значения, получим практически ту же оценку, что и раньше:

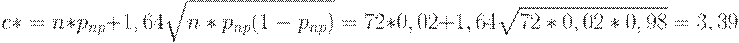
Итак, в результате асимптотических расчетов найден одноступенчатый план (72, 3).