Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рассмотрим как пример Площадь поверхности тора
|
|
В двух словах, тор – это бублик. Хрестоматийный пример, рассматриваемый практически во всех учебниках по матану, посвящён нахождению объёма тора, и поэтому в целях разнообразия я разберу более редкую задачу о площади его поверхности. Сначала с конкретными числовыми значениями:
Пример 1
Вычислить площадь поверхности тора, полученного вращением окружности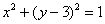 
вокруг оси 
.
Решение: как вы знаете, уравнение 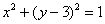задаёт окружность единичного радиуса с центром в точке 
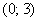. При этом легко получить две функции:
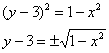
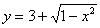– задаёт верхнюю полуокружность;
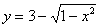– задаёт нижнюю полуокружность:
Суть кристально прозрачна: окружность вращается вокруг оси абсцисс и образует поверхность бублика. Единственное, здесь во избежание грубых оговорок следует проявить аккуратность в терминологии: если вращать круг, ограниченный окружностью 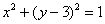, то получится геометрическое тело, то есть сам бублик. И сейчас разговор о площади его поверхности, которую, очевидно, нужно рассчитать как сумму площадей:
1) Найдём площадь поверхности, которая получается вращением «синей» дуги 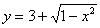вокруг оси абсцисс. Используем формулу 
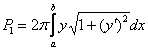. Как я уже неоднократно советовал, действия удобнее проводить поэтапно:
Берём функцию 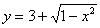и находим её производную:
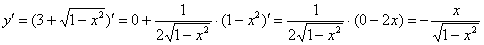
Далее максимально упрощаем корень:
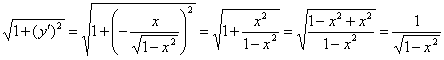
И, наконец, заряжаем результат в формулу:
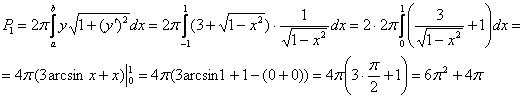
Заметьте, что в данном случае оказалось рациональнее удвоить интеграл от чётной функции по ходу решения, нежели предварительно рассуждать о симметрии фигуры относительно оси ординат.
2) Найдём площадь поверхности, которая получается вращением «красной» дуги 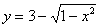вокруг оси абсцисс. Все действия будут отличаться фактически только одним знаком. Оформлю решение в другом стиле, который, само собой, тоже имеет право на жизнь:
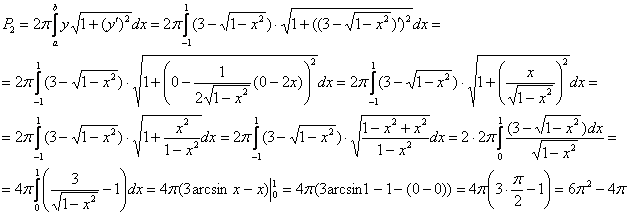
3) Таким образом, площадь поверхности тора:
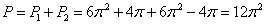
Ответ: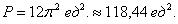 
Задачу можно было решить в общем виде – вычислить площадь поверхности тора, полученного вращением окружности 
вокруг оси абсцисс, и получить ответ 
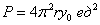. Однако для наглядности и бОльшей простоты я провёл решение на конкретных числах.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Если вам необходимо рассчитать объём самого бублика, пожалуйста, обратитесь к учебнику, в качестве экспресс-справки: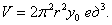 
Что только мы не делали с параболой за годы обучения, поэтому было бы большим упущением не покрутить её в своё удовольствие:
Пример 2
Вычислить площадь сферы, полученной вращением окружности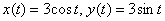 
вокруг оси .
Решение: из материалов статьи о площади и объемё при параметрически заданной линии вы знаете, что уравнения 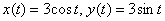задают окружность с центром в начале координат радиуса 3.
Ну а сфера, для тех, кто забыл, – это поверхность шара (или шаровая поверхность).
Придерживаемся наработанной схемы решения. Найдём производные:
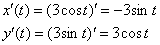
Составим и упростим «формульный» корень:
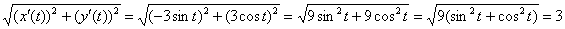
Что и говорить, получилась конфетка. Ознакомьтесь для сравнения, как Фихтенгольц бодался с площадью эллипсоида вращения.
Согласно теоретической ремарке, рассматриваем верхнюю полуокружность. Она «прорисовывается» при изменении значения параметра в пределах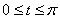 
(легко видеть, что 
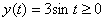на данном промежутке), таким образом:
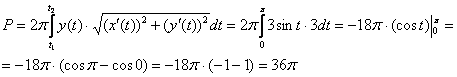
Ответ: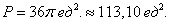 
Если решить задачу в общем виде, то получится в точности школьная формула площади сферы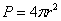 
, где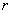 
– её радиус.
Пример 3
Вычислить площадь поверхности, образованной вращением кардиоиды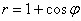 
вокруг полярной оси.
Решение: график данной кривой можно посмотреть в Примере 6 урока о полярной системе координат. Кардиоида симметрична относительно полярной оси, поэтому рассматриваем её верхнюю половинку на промежутке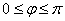 
(что, собственно, обусловлено и вышесказанным замечанием).
Поверхность вращения будет напоминать яблочко.
Техника решения стандартна. Найдём производную по «фи»:
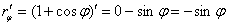
Составим и упростим корень:
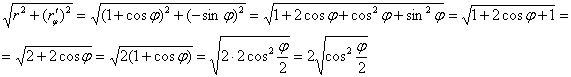
Надеюсь, с заштатными тригонометрическими формулами ни у кого не возникло затруднений.
Используем формулу:
На промежутке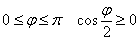 
, следовательно: 
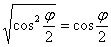(о том, как правильно избавляться от корня, я подробно рассказал в статье Длина дуги кривой).
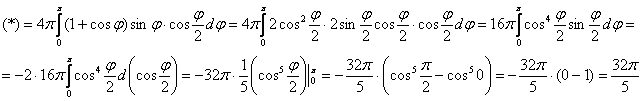
Ответ: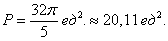 
Пример 4: Решение: вычислим площадь поверхности, образованной вращением верхней ветви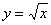 
вокруг оси абсцисс. Используем формулу 
.
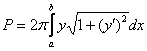В данном случае: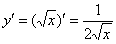 
;
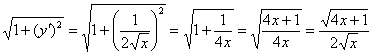
Таким образом:
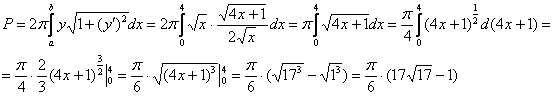
Ответ: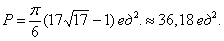 
Пример 5
Вычислить площадь шарового пояса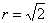 
, 
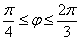
Решение: используем формулу:
Ответ: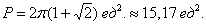 
3)
Фигуру можно вращать 2-мя способами.
– вокруг оси абсцисс;
– вокруг оси ординат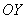
Пример 1
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями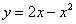 
, 
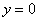вокруг оси .
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости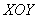 
необходимо построить фигуру, ограниченную линиями 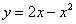, , 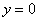при этом не забываем, что уравнение 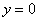задаёт ось
Объем тела вращения можно вычислить по формуле:
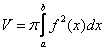
В формуле перед интегралом обязательно присутствует число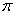 
. Так повелось – всё, что в жизни крутится, связано с этой константой.
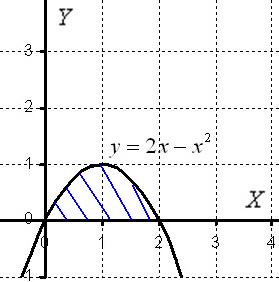
Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.
Функция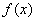 
… что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболы 
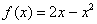сверху. Это и есть та функция, которая подразумевается в формуле.
В практических заданиях плоская фигура иногда может располагаться и ниже оси . Это ничего не меняет – подынтегральная функция в формуле возводится в квадрат: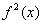 
, таким образом интеграл всегда неотрицателен, что весьма логично.
Вычислим объем тела вращения, используя данную формулу:
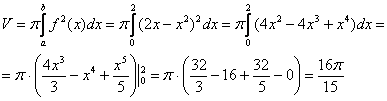
Как я уже отмечал, интеграл почти всегда получается простой, главное, быть внимательным.
Ответ: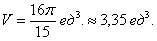 
Пример 2
Дана плоская фигура, ограниченная линиями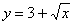 
, 
, 
.
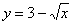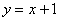1) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси .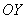
Выполним чертёж:
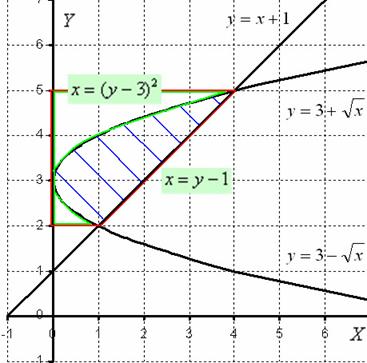
Итак, фигура, заштрихованная синим цветом, вращается вокруг оси 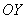. В результате получается «зависшая бабочка», которая вертится вокруг своей оси.
Для нахождения объема тела вращения будем интегрировать по оси 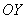. Сначала нужно перейти к обратным функциям. Это уже сделано и подробно расписано в предыдущем пункте.
Теперь снова наклоняем голову вправо и изучаем нашу фигуру. Очевидно, что объем тела вращения, следует найти как разность объемов.
Вращаем фигуру, обведенную красным цветом, вокруг оси 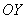, в результате получается усеченный конус. Обозначим этот объем через 
.
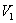Вращаем фигуру, обведенную зеленым цветом, вокруг оси 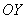и обозначаем через 
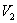объем полученного тела вращения.
Объем нашей бабочки равен разности объемов 
.
Используем формулу для нахождения объема тела вращения:
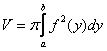
В чем отличие от формулы предыдущего параграфа? Только в букве.
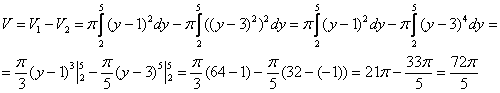
А вот и преимущество интегрирования, о котором я недавно говорил, гораздо легче найти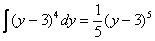 
, чем предварительно возводить подынтегральную функцию в 4-ую степень.
Ответ: 
Пример 3
Вычислить объем тела, образованного вращением вокруг оси 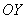фигуры, ограниченной кривым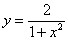и 
и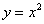 
.
Решение: Выполним чертеж:
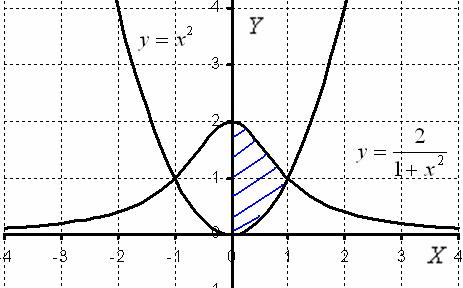
Попутно знакомимся с графиками некоторых других функций. Такой вот интересный график чётной функции ….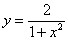
Для цели нахождения объема тела вращения достаточно использовать правую половину фигуры, которую я заштриховал синим цветом. Обе функции являются четными, их графики симметричны относительно оси 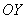, симметрична и наша фигура. Таким образом, заштрихованная правая часть, вращаясь вокруг оси 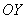, непременно совпадёт с левой нештрихованной частью.
Перейдем к обратным функциям, то есть, выразим «иксы» через «игреки»:
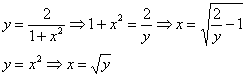
Обратите внимание, что правой ветке параболы 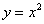соответствует обратная функция 
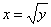. Левой неиспользуемой ветке параболы соответствует обратная функция 
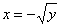. В таких случаях нередко возникают сомнения, какую же функцию выбрать? Сомнения легко, развеиваются, возьмите любую точку правой ветки и подставьте ее координаты в функцию 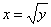. Координаты подошли, значит, функция 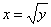задает именно правую ветку, а не левую.
К слову, та же история и с функций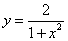 
. Чайнику, не всегда бывает сразу понятно, какую обратную функцию выбрать: 
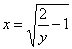или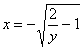 
. В действительности я и сам всегда страхуюсь, подставляя в найденную обратную функцию пару точек графика.
Теперь наклоняем голову вправо и замечаем следующую вещь:
– на отрезке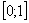 
над осью 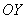расположен график функции ;
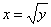– на отрезке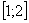 
над осью 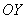расположен график функции ;
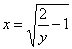Логично предположить, что объем тела вращения нужно искать уже как сумму объемов тел вращений!
Используем формулу:
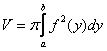
В данном случае:
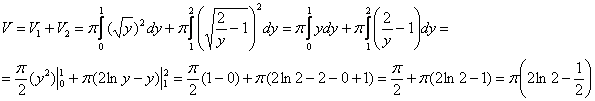
Ответ: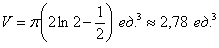 
Пример 4:
: Выполним чертеж:
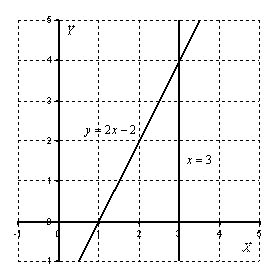
Объем тела вращения:
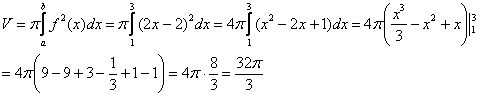
Ответ: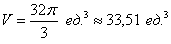 
Пример 5:
Выполним чертеж:
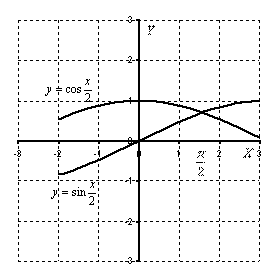
Объем тела вращения вычислим как разность объемов при помощи формулы:
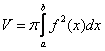
В данном случае:
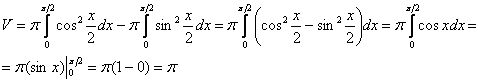
Ответ: 
|
|