
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод найменших квадратів для побудови градуювальної характеристики.
|
|
При експериментальному вивченні функціональної залежності однієї величини у від іншої величини х роблять ряд вимірювань величини у при різноманітних значеннях величини х. Результати вимірювань можуть бути подані на графіку у виді точок (х1, у1), (х2, у2),... (хn, уn). Ставиться задача підбору формули, що описує результати експерименту. Особливість задачі складається в тому, що наявність випадкових помилок вимірювання робить недоцільним підбір такої формули, що точно описувала б усі експериментальні значення. Іншими словами, графік, що відповідає підібраній формулі, не повинний проходити через всі експериментальні точки. Для виключення впливу помилок, роблять велике число вимірювань. Запишемо обрану функціональну залежність у вигляді:
y=f(x, a0, a1,..., an), (2.1)
де x - незалежна змінна;
а0, а1,..., аn - постійні параметри. Постійні параметри невідомі і підлягають визначенню. Для їх знаходження проводиться ряд вимірювань величин х і у. Підставляючи їх у рівність (1) одержимо рівняння вигляду:
yi=f(xi, a0, a1,..., am), (2.2)
де xi, yi - відповідні одне одному обмірювані значення;
i=1, 2,..., m;
m - кількість вимірювань.
Якби значення х і у знаходилися точно, то для опису m+1 параметра достатньо було б зробити m+1 вимірювань. Насправді, значення х і у містять випадкові помилки, тому промова може йти тільки про одержання " достатньо гарних" оцінок шуканих параметрів. Іншими словами, необхідно знайти найбільше ймовірні значення невідомих параметрів. Ці ймовірні значення будуть тим більше близькі до істинних, чим більше число виконаних спостережень.
Через те що рівняння (2.2) задовольняється неточно, то будемо мати:
y-f(xi, a0, a1,..., am)=di,
де d - відхилення виміряних значень yi від обчислених за формулою (2.2).
Принцип найменших квадратів підтверджує, що найімовірнішими значеннями параметрів будуть такі, при яких сума квадратів відхилень di буде найменшої, тобто
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
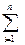 yi-f(xi, a0, a1,..., am)]2=min. (2.3)
yi-f(xi, a0, a1,..., am)]2=min. (2.3)
Розглядаємо а0, а1,..., аm як незалежні змінні і прирівнюючи до " 0" частні похідні від лівої частини по цим змінним, одержимо m+1 рівняння з m+1 невідомим.
У даному випадку функціональна залежність має вигляд: y=a0+a1*x
Вираження, що визначає суму квадратів різниці виміряного значення і розрахункового, запишемо у вигляді 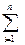 yi-(a0+a1*x1)]2=
yi-(a0+a1*x1)]2= 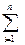 s2i. Продиференціювавши дане вираження послідовно по а0 і а1 і прирівнявши отримані вираження до нуля, одержимо систему рівнянь
s2i. Продиференціювавши дане вираження послідовно по а0 і а1 і прирівнявши отримані вираження до нуля, одержимо систему рівнянь
n*a0+a1* 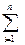 xi=
xi= 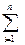 yi
yi
a0* 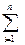 xi+a1*
xi+a1* 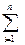 xi2=
xi2= 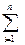 yi*xi
yi*xi
Вирішуючи дану систему рівнянь щодо а0 і а1, отримуємо
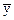 *
* 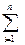 xi2 -
xi2 - 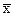 *
* 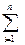 yi*xi
yi*xi
a0= (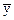 *
* 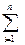 xi2 -
xi2 - 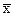 *
* 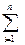 yi*xi)/(
yi*xi)/(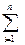 xi2 -
xi2 - 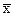 *
* 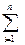 xi);
xi);
a1=(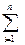 xi*yi -
xi*yi - 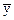 *
* 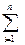 xi)/ (
xi)/ (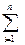 xi2 -
xi2 - 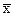 *
* 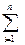 xi);
xi);
де 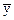 = (1/n)*
= (1/n)* 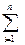 yi;
yi; 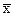 = (1/n)*
= (1/n)* 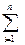 xi.
xi.
|
|
