Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Краткая теория. Цель работы – определение моментов инерции различных тел, проверка теоремы Штейнера.

Лабораторная работа №14

МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ИЗУЧЕНИЕ ТЕОРЕМЫ ШТЕЙНЕРА ПРИ ПОМОЩИ УНИВЕРСАЛЬНОЙ УСТАНОВКИ КОБРА 3

Цель работы – определение моментов инерции различных тел, проверка теоремы Штейнера.

Приборы и принадлежности

Установка Кобра 3, световой барьер, устройство для изучения крутильных колебаний, держатель для гирь, гири, нить.

Краткая теория

При малых амплитудах колебаний возвращающий момент пропорционален углу отклонения от положения равновесия. Следовательно, получаем гармонические круговые колебания с частотой

.

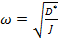Модуль кручения D ^* определяется параметрами спиральной пружины. Период колебания тела

определяется при помощи секундомера. Неизвестный момент инерции можно рассчитать из значений для модуля кручения D ^* и периода колебаний T при помощи выражения:

.

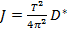Анализ формул позволяет вывести следующую зависимость моментов инерции J тел:

Круглый диск:

Момент инерции J круглого диска зависит от массы m и радиуса r диска:

.

Полый и цельный цилиндр:

Момент инерции J_V полого цилиндра зависит от его массы m_V и радиуса r:

.

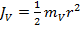Для полого цилиндра такой же массы и внешним радиусом момент инерции будет больше. Он зависит как от массы m_H полого цилиндра, так и от радиусов r_i и r_a:

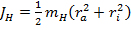(для полого цилиндра).

Через плотность материала ρ и высоту h масса полого цилиндра выражается как

.

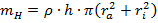Выражение для расчета момента инерции J_H имеет вид:

,

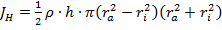преобразовав которое, получаем:

.

з данного выражения видно, что момент инерции полого цилиндра может выражаться как момент инерции двух цельных цилиндров с одинаковой плотностью. Масса большего цельного цилиндра с радиусом r_a равна:

,

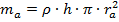а масса меньшего цельного цилиндра с радиусом r_i равна:

.

Таким образом, получаем:

.

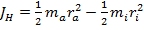Сфера:

Момент инерции J_K однородного сферического тела по отношению к оси, проходящей через его центральную точку, равна:

.

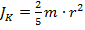Таким образом, момент инерции цилиндра с тем же радиусом r и той же массой m больше, чем момент инерции сравниваемой сферы.

В таблице 1 наряду со значениями массы и размеров тел представлены табличные значения моментов инерции и значения, полученные экспериментальным путем.

Стержень с подвижными гирями:

Момент инерции стержня с подвижными гирями зависит от расстояния между гирями и осью вращения. Полученные моменты инерции стержня без подвижных гирь и с ними, которые расположены в различных точках стержня, а также вычисленные значения момента инерции стержня представлены в таблице 2:

,

момент инерции гирь без стержня:

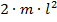
а сумма моментов инерции стержня и гирь:

.

Каждый раз измеренный момент инерции соответствует сумме отдельных моментов инерции.

Для проводимых измерений использовались следующие параметры:

Длина стержня 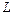60 см

Масса 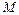стержня 0, 1715 кг

Масса одной гири 0, 2115 кг

Теорема Штейнера:

Согласно теореме Штейнера, общий момент инерции J тела, вращающегося вокруг произвольной оси, равен:

,

где J₀ - момент инерции относительно оси, параллельной оси вращения и проходящей через центр масс (ось гравитации), r ² - квадрат расстояния между осью вращения и осью гравитации.

В таблице 3 представлены значения момента инерции полученные экспериментально J _измер и соответствующие теоретические .

Таблица 1

Тело	m, кг	r, см	J, кг·см2	JT, кг·см2
Диск	0, 292		17, 42	17, 66
Цельный цилиндр	0, 370	4, 9	4, 78	4, 44
Полый цилиндр	0, 390	:	8, 15	7, 49

Таблица 2

Таблица 3 (масса диска m = 0, 454 кг)