Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сканер 200

США

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

1) заметим, что в силу тождества 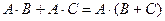последний запрос в таблице равносилен такому:

(США & Япония) | (США & Китай) Û США & (Япония | Китай)

2) тогда вводя обозначение для областей

A = США, B = Япония | Китай,

получаем стандартную задачу с двумя переменными:

3) имеем по формуле (см. решения ниже)

N_A = N_A|B - N_B + N_{A& B} = 450 – 260 + 50 = 240

4) Ответ: 240

Ещё пример задания:

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Сколько страниц (в тысячах) будет найдено по запросу

Ростов & Орёл & Курск

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

5) заметим, что во всех четырёх запросах есть «сомножитель» «Ростов &», поэтому эта задача равносильна такой:

6) теперь обозначим A = Орёл & Курск и получим задачу с двумя областями:

7) по формуле для задачи с двумя областями (см. задачи, разобранные ниже)

N_A|B = N_A + N_B - N_{A& B}

получаем

N_A = N_A|B - N_B + N_{A& B}

8) вычисляем: 370 – 204 + 68 = 234.

9) Ответ: 234.

Ещё пример задания:

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Сколько страниц (в тысячах) будет найдено по запросу

Подкова & Наковальня

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение (вариант 1, рассуждения по диаграмме):

10) построим диаграмму Эйлера-Венна

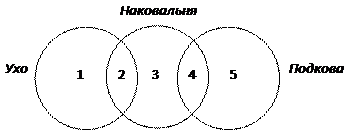
11) количество сайтов, удовлетворяющих запросу в области i, будем обозначать через N_i

12) здесь 5 областей, причём известны следующие данные:

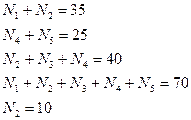
13) нас интересует область 4. Находим ответ прямой подстановкой:

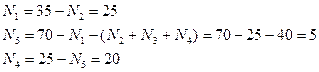
14) таким образом, ответ – 20.

Решение (вариант 2, рассуждения по диаграмме):

1) пп. 1-2 такие же, как в варианте 1

2) заметим, что в прямую сумму величин областей Ухо, Подкова и Наковальня дважды входят области 2 и 4, поэтому для вычисления 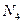достаточно вычесть из суммы Ухо+Подкова+Наковальня размер их объединения (Ухо | Подкова | Наковальня) и величину области 2 (Ухо & Наковальня).

3) тогда сразу получаем

.

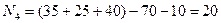4) ответ – 20.

Еще пример задания:

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Сколько страниц (в тысячах) будет найдено по запросу

пирожное | выпечка

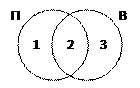Решение (вариант 1, рассуждения по диаграмме):

5) построим диаграмму Эйлера-Венна, обозначив области «пирожное» (через П) и «выпечка» (В):

6) количество сайтов, удовлетворяющих запросу в области i, будем обозначать через N_i

7) несложно сообразить, что число сайтов в интересующей нас области равно

N₁ + N₂ + N₃ = (N₁ + N₂) + (N₃ + N₂) – N₂

8) поскольку нам известно, что по условию

N₁ + N₂ = 8700

N₃ + N₂ = 7500

N₂ = 3200

сразу получаем

N₁ + N₂ + N₃ = 8700 + 7500 - 3200 = 13000

9) таким образом, ответ – 13000.

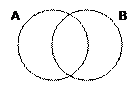Решение (вариант 2, общая формула):

1) сначала выведем формулу, о которой идет речь; построим диаграмму Эйлера-Венна для двух переменных A и B:

2) обозначим через N_A, N_B, N_{A& B} и N_A|B число страниц, которые выдает поисковый сервер соответственно по запросам A, B, A & B и
A | B

3) понятно, что если области A и B не пересекаются, справедлива формула N_A|B=N_A+N_B

4) если области пересекаются, в сумму N_A+N_B область пересечения N_{A& B} входит дважды, поэтому в общем случае

N_A|B = N_A + N_B - N_{A& B}

5) в данной задаче

N_П = 8700, N_В = 7500, N_{П& В} = 3200

6) тогда находим число сайтов в интересующей нас области по формуле

N_П|B = N_П + N_B – N_{П& B} = 8700 + 7500 – 3200 = 13000

7) таким образом, ответ – 13000.

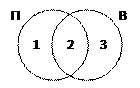Решение (вариант 3, решение системы уравнений):

1) нарисуем области «пирожное» (обозначим ее через П) и «выпечка» (В) в виде диаграммы (кругов Эйлера); при их пересечении образовались три подобласти, обозначенные числами 1, 2 и 3;

2) составляем уравнения, которые определяют запросы, заданные в условии:

пирожное & выпечка N₂ = 3200

пирожное N₁ + N₂ = 8700

выпечка N₂ + N₃ = 7500

3) подставляя значение N₂ из первого уравнения в остальные, получаем

N₁ = 8700 - N₂ = 8700 – 3200 = 5500

N₃ = 7500 - N₂ = 7500 – 3200 = 4300

4) количество сайтов по запросу пирожное | выпечка равно

N₁ + N₂ + N₃ = 5500 + 3200 + 4300 = 13000

5) таким образом, ответ – 13000.

Еще пример задания:

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Сколько страниц (в тысячах) будет найдено по запросу

Рубин & Динамо & Спартак

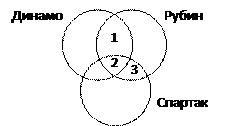Решение (вариант 1, круги Эйлера, полная диаграмма):

1) в этой задаче неполные данные, так как они не позволяют определить размеры всех областей; однако их хватает для того, чтобы ответить на поставленный вопрос

2) обозначим области, которые соответствуют каждому запросу

3) из таблицы следует, что в суммарный результат первых двух запросов область 2 входит дважды (1 + 2 + 2 + 3), поэтому, сравнивая этот результат с третьим запросом (1 + 2 + 3), сразу находим результат четвертого:

N₂ = (320 + 280) – 430 = 170

4) таким образом, ответ – 170.

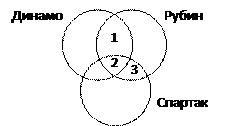Решение (вариант 2, круги Эйлера, неполная диаграмма):

1) заметим, что в этой задаче все запросы (в том числе и тот, результат которого нужно найти, имеют вид

X & Рубин

2) поэтому часть «& Рубин» в каждом из запросов можно просто отбросить, тогда останется только две области:

здесь добавление «-1» в имени области обозначает «пересечение с областью Рубин»

3) требуется найти размер области «Динамо-1 & Спартак-1»

4) для диаграммы с двумя областями можно использовать общую формулу

N_A|B = N_A + N_B - N_{A& B}

5) из которой следует

N_{A& B} = N_A + N_B - N_A|B

6) в данном случае получаем

N_{A& B} = (320 + 280) – 430 = 170

7) таким образом, ответ – 170.

Ещё пример задания:

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.

1) принтеры & сканеры & продажа

2) принтеры & сканеры

3) принтеры | сканеры

4) принтеры | сканеры | продажа

Решение (вариант 1, рассуждение с использованием свойств операций «И» и «ИЛИ»):

1) меньше всего результатов выдаст запрос с наибольшими ограничениями – первый (нужны одновременно принтеры, сканеры и продажа)

2) на втором месте – второй запрос (одновременно принтеры и сканеры)

3) далее – третий запрос (принтеры или сканеры)

4) четвертый запрос дает наибольшее количество результатов (принтеры или сканеры или продажа)

5) таким образом, верный ответ – 1234.

Решение (вариант 2, через таблицы истинности):

1) каждое из условий можно рассматривать как сложное высказывание

2) обозначим отдельные простые высказывания буквами:

A: принтеры (на странице есть слово «принтеры»)

B: сканеры

C: продажа

3) запишем все выражения-запросы через логические операции

, , ,

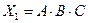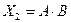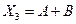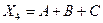
4) здесь присутствуют три переменные, А, B и C (хотя второе и третье выражения от С не зависят!), поэтому для составления таблицы истинности нужно рассмотреть 8 = 23²³³³ всевозможных комбинаций этих логических значений

5) выражение 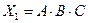равно 1 (истинно) только при 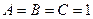, в остальных случаях – равно 0 (ложно)

6) выражение 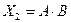равно 1 только при 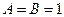, в остальных случаях – равно 0

7) выражение 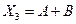равно 0 только при 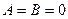, в остальных случаях – равно 1

8) выражение 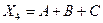равно 0 только при 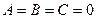, в остальных случаях – 1

9) запишем результаты пп. 5-8 в виде таблицы истинности

A	B	C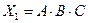

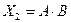
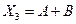
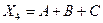
10) по таблице видим, что наименьшая «область действия» у первого выражения, поисковый сервер выдаст наименьшее число запросов

11) область, где 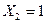, включает в себя[1] всю область, где 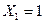и еще один вариант, поэтому «поисковик» выдаст больше запросов, чем для первого случая

12) аналогично делаем вывод, что область 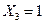включает всю область 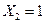и расширяет ее, а область 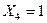– это расширение области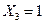

13) таким образом, верный ответ – 1234.

Решение (вариант 3, через диаграммы):

1) запишем все ответы через логические операции

, , ,

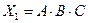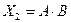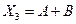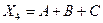
2) покажем области, определяемые этими выражениями, на диаграмме с тремя областями

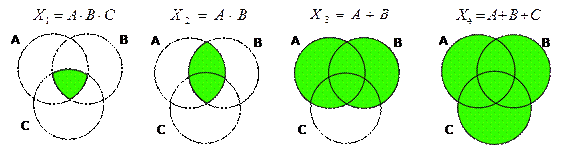
3) сравнивая диаграммы, находим последовательность областей в порядке увеличения: (1, 2, 3, 4), причем каждая следующая область в этом ряду охватывает целиком предыдущую (как и предполагается в задании, это важно!)

4) таким образом, верный ответ – 1234.

Еще пример задания:

Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:

Сколько сайтов будет найдено по запросу

(принтер | сканер) & монитор

если по запросу принтер | сканер было найдено 450 сайтов, по запросу принтер & монитор – 40, а по запросу сканер & монитор – 50.

Решение (вариант 1, использованием свойств операций «И» и «ИЛИ»):

1) обратим внимание на такой факт[2] (справа указано количество сайтов по каждому запросу)

сканер 200