Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

If n < 6 then begin

Begin

writeln(n);

If n < 5 then begin

F(n + 1);

F(n + 3)

End

end;

Найдите сумму чисел, которые будут выведены при вызове F(1).

Решение (вариант 1, построение дерева вызовов):

1) поскольку в начале каждого вызова на экран выводится значение единственного параметра функции, достаточно определить порядок рекурсивных вызовов и сложить значения параметров

2) поскольку при выполняется два рекурсивных вызова, решать такую задачу «на бумажке» удобно в виде двоичного дерева (в узлах записаны значения параметров при вызове функции):

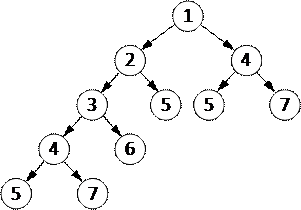
3) складывая все эти числа, получаем 49

4) ответ: 49.

Решение (вариант 2, подстановка):

1) можно обойтись и без дерева, учитывая, что при каждом вызове с n < 5 происходит два рекурсивных вызова; сумму чисел, полученных при вызове , обозначим через :

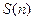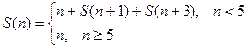
2) выполняем вычисления:

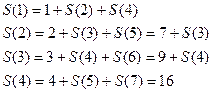
3) теперь остаётся вычислить ответ «обратным ходом»:

4)

5) Ответ: 49.

Ещё пример задания:

Дан рекурсивный алгоритм:

procedure F(n: integer);

Begin

writeln(n);

if n < 6 then begin

F(n+2);

F(n*3)

End

end;

Найдите сумму чисел, которые будут выведены при вызове F(1).

Решение (вариант 1, метод подстановки):

6) сначала определим рекуррентную формулу; обозначим через G(n) сумму чисел, которая выводится при вызове F(n)

7) при n > = 6 процедура выводит число n и заканчивает работу без рекурсивных вызовов:

G(n) = n при n > = 6

8) при n < 6 процедура выводит число n и дважды вызывает сама себя:

G(n) = n + G(n+2) + G(3n) при n < 6

9) в результате вызова F(1) получаем

G(1) = 1 + G(3) + G(3)

G(3) = 3 + G(5) + G(9) = 3 + G(5) + 9

G(5) = 5 + G(7) + G(15) = 5 + 7 + 15 = 27

10) используем обратную подстановку:

G(3) = 3 + G(5) + 9 = 3 + 27 + 9 = 39

G(1) = 1 + 2*G(3) = 79

11) Ответ: 79.

Решение (вариант 2, динамическое программирование):

1) п. 1-3 такие же, как в первом варианте решения

2) заполняем таблицу G(n) при n > = 6 (где G(n) = n)

3) остальные ячейки заполняем, начиная с n = 5 справа налево, используя формулу:

G(n) = n + G(n+2) + G(3n)

4) ответ читаем в самой левой ячейке

5) Ответ: 79.

Пример задания:

Дан рекурсивный алгоритм:

procedure F(n: integer);

Begin

writeln('*');