
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лабораторная работа №4. Цель лабораторной работы: освоить технику проверки гипотезы о виде закона распределения генеральной совокупности
|
|
ТЕМА: ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ ПО КРИТЕРИЮ ПИРСОНА.
Цель лабораторной работы: освоить технику проверки гипотезы о виде закона распределения генеральной совокупности, используя критерий Пирсона.
Задание:
Использовать выборку из 1лаб.работы и сделать теоретические частоты.
Найдем середины интервалов и примем их в качестве вариант для расчета числовых характеристик. n =ni= 200
Определим 
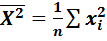 *
* 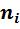
Дисперсия D=  -
- 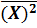
Ср.квад. отклонение σ = 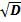
Найдем теоретические частоты. Для этого пронормируем данную случайную величину X и перейдем к величине Z, Z=X- x/ σ.
Затем найдем теоретические вероятности, пользуясь формулой
P =Φ (Zi+1) − Φ (Zi)+, Φ (z) – функция Лапласа
Проверить согласно гипотезе критерию Пирсона о нормальности распределения.
Сравним эмпирические и теоретические частоты, используя критерий Пирсона. Вычислим наблюдаемое значение критерия Пирсона по формуле
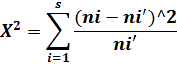
Необходимым условием применения критерия Пирсона является наличие в каждом из интервалов не менее 5 наблюдений. Однако, учитывая, что первые три интервала содержат малочисленные частоты, объединим их, а соответствующие частоты и теоретические частоты сложим. Данные расчетов приведем в таблице.
По таблице критических точек распределения (приложение 5), по уровню значимости α =0, 05 и числу степеней свободыk = s − 1 = 30-1 = 29 (s – число интервалов) находим критическую точку правосторонней критической области(0, 05; 0.01). Так как χ 2< χ 2кр, то гипотезу о нормальном распределении генеральной совокупности принимаем.
Пример задания:
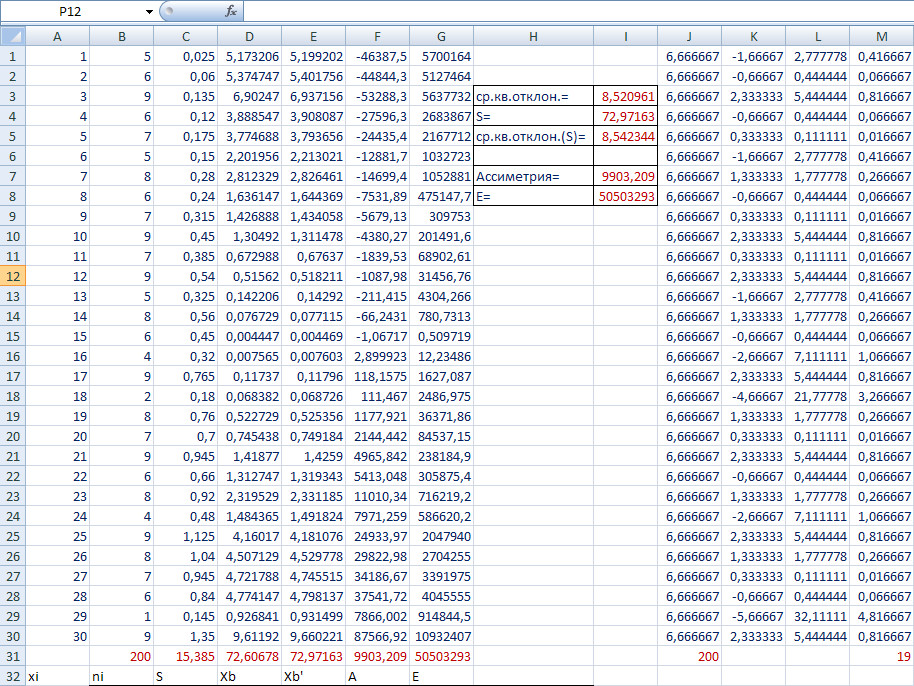
1. 
2. 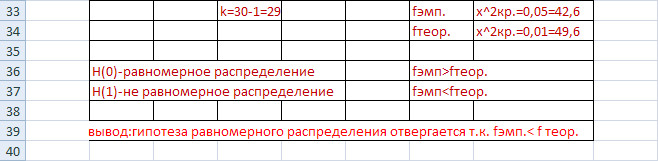
Вывод: fэмп.< X^2 для 0, 01, то Н0 отвергается. Гипотеза равномерного распределения отвергается т.к. fэмп.< fтеор.
|
|
