
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
I I I. Преобразование тригонометрических выражений.
|
|
А1. Вычислите: 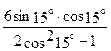 1) 3
1) 3  2)
2)  3) 1, 5
3) 1, 5 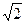 4) 0.
4) 0.
А1. Вычислите cos215° - sin215° 1) - 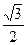 2)
2) 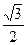 3)
3) 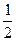 4)
4) 
А1. Вычислите 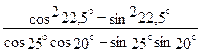 1) -1 2)
1) -1 2)  3)
3) 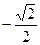 4) 1
4) 1
А1. Вычислите 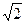 sin22, 5° cos22, 5° 1) 1 2)
sin22, 5° cos22, 5° 1) 1 2) 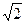 3)
3)  4)
4) 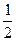
А2. Найдите значение выражения  . 1) -3 2) 2 3) -2 4) 3
. 1) -3 2) 2 3) -2 4) 3
A2. Найдите значение выражения 2sinπ + 3cosπ + ctg 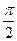 1) -3 2) 1 3) -1 4) 0
1) -3 2) 1 3) -1 4) 0
A2. Найдите значение выражения sin 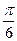 ∙ sin
∙ sin 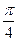 ∙ sin
∙ sin 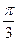 ∙ sinπ 1) 0 2)
∙ sinπ 1) 0 2) 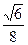 3)
3) 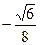 4)
4) 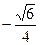
A2. Найдите значение выражения tg 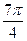 –2 sin
–2 sin 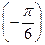 – cos3π 1)
– cos3π 1)  2) 1 3)
2) 1 3)  – 2 4) –
– 2 4) – 
А3. Упростите выражение: cos2(π – α) + cos2(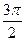 – α) 1) 1 2) 2cos2α 3) 2 sin2α 4) 0
– α) 1) 1 2) 2cos2α 3) 2 sin2α 4) 0
А3.Упростите выражение: sin3α cos2α + sin2α cos3α – cos(2π – α)
1) sin5α + cosα 2) sinα + cosα 3) sin5α – cosα 4) sinα – cosα
А3. Упростите выражение: sin3, 5α sin2, 5α – cos3, 5α cos2, 5α + cos(4π + α)
1) cosα + cos6α 2) 0 3) 2cosα 4) – cos6α + cosα
А3. Упростите выражение: sin3α sin2α – cos3α cos2α – cos(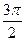 – α)
– α)
1) cos5α – sinα 2) – cos5α + sinα 3) – cos5α – sinα 4) 2 sinα
А4. Найдите значение выражения 3cos2x + 2, если sin2x = 0, 8. 1) 3, 08 2) 7, 4 3) 1, 6 4) 2, 6
А4. Найдите значение выражения 3sin2x - 1, если cos2x = 0, 5. 1) 0, 5 2) -1, 5 3) 1, 25 4) -0, 5
А4. Найдите значение выражения 2cos2x - 1, если sin2x = 0, 3. 1) 0, 4 2) -0, 3 3) 0, 82 4) 0, 7
В1. Найдите значение выражения 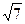 tgα ∙ sin
tgα ∙ sin  , если sinα =
, если sinα = 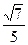 .
.
В1. Найдите значение выражения 2 sin2α + 6 cos2α, если sin α = - 0, 2.
В1. Найдите значение выражения 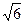 tg α · cos (π + α), если sin α =
tg α · cos (π + α), если sin α = 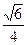 .
.
В1. Найдите значение выражения 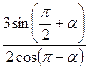 . если α =
. если α = 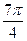 .
.
В6. 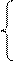 Найдите значение функции f(х) =
Найдите значение функции f(х) = 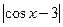 , если
, если 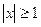
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
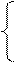 sin(-x), если
sin(-x), если 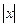 < 1. при х = -
< 1. при х = - 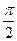
В6. Найдите значение функции f(х) =  , если
, если 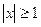
cosx, если 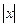 < 1. при х =
< 1. при х = 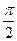
В6. Найдите значение tg α, если cos α =  и -
и - 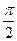 < α < 0.
< α < 0.
В6. Зная, что sinα = 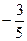 , π < α <
, π < α < 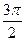 , найдите tg(
, найдите tg(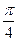 + α)
+ α)
ПРОИЗВОДНАЯ
А 8. Найдите точку максимума функции f (х) = х3 – 3 х2. 1) 0 2) 2 3) – 2 4) 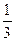
А 8. Найдите точку минимума функции у = х2 – 1 1) 0 2) – 1 3) 1 4) 0, 5
А 8. Найдите точку максимума функции у = 4х – х4. 1) 0 2) – 1 3) 1 4) – 2
А 8. Решите уравнение f׳ (х) = 0, если f(х) = (3х2 + 1)∙ (3х2 – 1). 1) ±  2) 2 3) ±
2) 2 3) ±  4) 0.
4) 0.
А 10. Найдите тангенс угла наклона касательной, проведённой к графику функции у = - 0, 5х2 в его точке с абсциссой х0 = - 3. 1) – 3 2) – 4, 5 3) 3 4) 0.
А 10. Найдите тангенс угла наклона касательной, проведённой к графику функции у = - 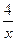 в его точке с абсциссой х0 = - 2. 1) 1 2) 2 3) 0 4) – 1.
в его точке с абсциссой х0 = - 2. 1) 1 2) 2 3) 0 4) – 1.
А 10. Вычислите скорость изменения функции g(х) = х3 + 2х в точке х0 = 2. 1) 14 2) 12 3) 8 4) 16.
А 10. Найдите значение производной функции у = x2 + sin x в точке х0 = π.
1) π 2 – 1 2) 2π + 1 3) 2π – 1 4) 2π
А 10. Найдите значение производной функции у = 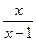 в точке х0 = 0. 1) 1 2) 0 3) 0, 5 4) - 1
в точке х0 = 0. 1) 1 2) 0 3) 0, 5 4) - 1
В2. Составьте уравнение касательной к графику функции f(х) = х2 + 2х в его точке с абсциссой х0 = -2. В ответе укажите координату по оси ординат точки с абсциссой равной – 3, 5
В2. Составьте уравнение касательной к графику функции f(х) = х2 + 1 в его точке с абсциссой х0 = 1. В ответе укажите координату по оси ординат точки с абсциссой равной – 5, 5
В2. Составьте уравнение касательной к графику функции f(х) = х2 – 4 в его точке с абсциссой х0 = -2. В ответе укажите координату по оси ординат точки с абсциссой равной – 1, 5
В2. Составьте уравнение касательной к графику функции f(х) = 2 – х2 в его точке с абсциссой х0 = -3. В ответе укажите координату по оси ординат точки с абсциссой равной – 2, 5
В 8. Решите неравенство f׳ (х) < 0, если f(х) = 2х3 – 6х. В ответе укажите число целых решений этого неравенства.
В 8. Решите неравенство f׳ (х) > 0, если f(х) = 6х2 – х3. В ответе укажите число целых решений этого неравенства.
В 8. Решите неравенство f׳ (х) ≥ 0, если f(х) = 7, 5х2 – х3. В ответе укажите число целых решений этого неравенства.
В 8. Решите неравенство f׳ (х) ≥ 0, если f(х) = 12х – х3. В ответе укажите число целых решений этого неравенства.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
В 4. Найдите наименьшее значение функции у = х3 + 3х2 – 4 на отрезке [-4; 1].
В 4. Найдите наименьшее значение функции у = 2х + 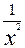 на отрезке [
на отрезке [ 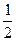 ; 3].
; 3].
В 4. Найдите наименьшее значение функции f(х) = 6х3 – 3х2 – 12х + 7 на отрезке [-1; 2].
В 4. Найдите наибольшее значение функции f(х) = х4 – 8х3 + 10х2 + 1 на отрезке [-1; 2]
В 4. Найдите наибольшее значение функции у = х – 2 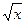 на промежутке [0: +∞).
на промежутке [0: +∞).
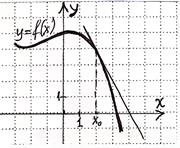
В1. На рисунке изображён график функции f(х) и касательная к нему в точке с абсциссой х0. Найдите f׳ (х) в точке х0.
1) -2
2) 2
3) 8
4) - 4
В1. На рисунке изображён график функции f(х) и касательная к нему в точке с абсциссой х0. Найдите f׳ (х) в точке х0.
1) 1
2) – 5
3) – 1
4) 5

В 10. Функция у = f(х) задана на отрезке [-5; 6]. На рисунке изображён график её производной у = f׳ (х). Исследуйте на монотонность функцию у = f(х). В ответе укажите количество промежутков, на которых функция убывает.

В 10. Функция у = f(х) задана на отрезке [а; в]. На рисунке изображён график её производной у = f׳ (х). Исследуйте на монотонность функцию у = f(х). В ответе укажите количество промежутков, на которых функция убывает.

В 10. Функция у = f(х) задана на отрезке [а; в]. На рисунке изображён график её производной у = f׳ (х). Исследуйте на монотонность функцию у = f(х). В ответе укажите количество промежутков, на которых функция убывает.
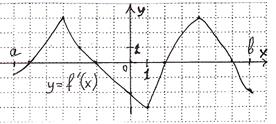
В 10. На рисунке изображён график производной функции у = f(х). Найдите число точек, в которых тангенс угла наклона касательной к этой функции равен 2.
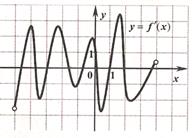
В 10. На рисунке изображён график производной функции
у = f(х). Найдите число точек экстремума этой функции.

В10. На рисунке изображён график производной функции
у = f(х). Найдите число промежутков возрастания этой функции.
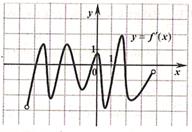
В10. На рисунке изображён график производной функции
у = f(х). Найдите число точек минимума этой функции.
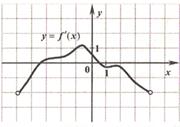
В10. Функция у = f(х) определена на интервале (- 6; 4). На рисунке изображён график её производной. Найдите точку а, в которой функция у = f(х) принимает наибольшее значение.
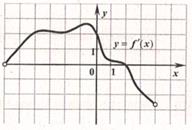
В10. Функция у = f(х) определена на интервале (- 6; 5). На рисунке изображён график её производной. Найдите длину промежутка убывания этой функции.
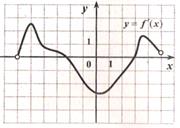
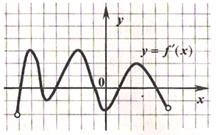
В 10. На рисунке изображён график производной функции у = f(х). В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох.
А10. При движении тела по прямой расстояние S (в метрах) от начальной точки движения изменяется по закону S(t) = 0, 5 t 2 - 4 t + 6 (t – время движения в секундах). Через сколько секунд тело остановиться?
1) 2 2) 4 3) 6 4) -4
А9. К графику функции у = Зх2 + 5х - 15 в точке хо=1/6 проведена касательная. Найдите тангенс угла наклона касательной к оси Ох.
1)6 2)11 3)7 4)4.
А8. Найдите производную функции у = 5 + 8 х7 + 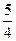 х4.
х4.
1) у ' = 5х + х8 + 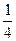 х5 2) у ' = 56х6 + 5х3 3) у ' = 5х + 15х6 + 5х3 4) у ' = х8 + 5х3
х5 2) у ' = 56х6 + 5х3 3) у ' = 5х + 15х6 + 5х3 4) у ' = х8 + 5х3
В3. При движении тела по прямой расстояние S(в метрах) от начальной точки движения изменяется по закону S(t) = t3 /3 –t2 + t - 1 (t - время движения в секундах). Найдите скорость (м/с) тела через 4 секунды после начала движения.
В3. Точка движется по координатной прямой согласно закону х(t) = t 2 + 2t + 9, где х(t) – координата точки в момент времени t. В какой момент времени скорость будет равна 12?
|
|
