Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Невозмущенное (кеплерово) орбитальное движение

В соответствии со вторым законом Ньютона движение центра масс спутника в инерциальной системе координат ОХо Y0Z0 описы­ вается уравнением

F = тg, (2.1)

где т - масса спутника; g - вектор центростремительного ускоре­ ния; F - вектор силы земного притяжения.

Первый закон Кеплера гласит, что любая траектория спутника, движущегося в центральном поле тяготения, лежит в неподвижной относительно инерциальной системы координат плоскости, проходящей через центр тяготения, и представляет собой кривую второго порядка, в одном из фокусов которой находится центр притяжения. Плоскость, в которой лежит траектория движения спутника, называется орбитальной плоскостью.

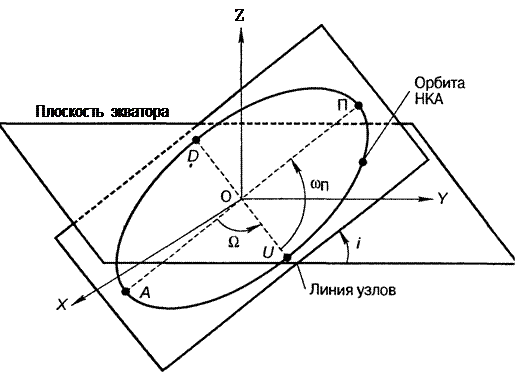
Элементы кеплеровой орбиты спутника

Проходящая через экватор плоскость ХОУ называется эквато­ риальной плоскостью. Ориентация орбитальной плоскости харак­ теризуется ее положением относительно экваториальной плоскости. Линия пересечения этих плоскостей называется линией узлов, а узлами орбиты спутника являются точки пересечения орбиты с экваториальной плоскостью. Узел U, образующийся при движении спутника из южной небесной полусферы в северную, называют восходящим, а узел D, образующийся при движении из северной небесной полусферы в южную - нисходящим.

Для однозначного определения положения орбитальной плоскости относительно экваториальной применяются два орбитальных элемента: долгота восходящего узла и наклонение орбиты.

Прямую линию, проходящую через фокусы эллипса О, называют линией апсид, а точки пересечения этой линии с эллипсом - апси­ дами. Ближайшую к центру полярной системы координат вершину (точка П) называют перицентром, а удаленную вершину (точка А) - апоцентром. Это обобщенные термины. Если спутник вращается по эллиптической орбите вокруг Земли, то эти точки называются соответственно перигей и апогей. Заметим, что точку апоцентра имеют только эллиптические орбиты.

Когда спутник движется по эллиптической орбите, его угловая скорость непостоянна и зависит от положения на орбите. Для вы­ числений удобнее использовать равномерное движение с постоянной угловой скоростью. С этой целью вводится угловой параметр М - средняя аномалия для момента времени t, или средняя аномалия эпохи t:

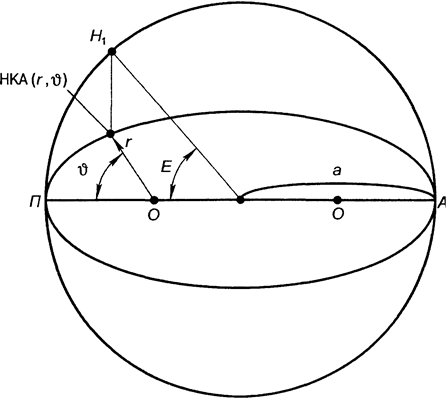
Геометрический смысл эксцентрической аномалии

Если период обращения спутника равен звездным суткам (Т = Тз), такие спутник относят к суточным, а при периоде обращения крат­ ном Тз к синхронным. Если площадь орбиты суточного спутника лежит в плоскости экватора, такой спутник называют геостацио­ нарным, так как он неподвижен относительно экватора.

Период обращения НКА ГЛОНАСС 11, 2 ч; НКА GPS NAVSTAR 12 ч. Таким образом, спутник GPS один раз в сутки проходит над одной и той же точкой на поверхности земли. Период обращения геостационарных спутников 23 ч 56 мин. 4, 091 с.

Форма орбиты спутника и ориентация орбитальной плоскости в инерциальной системе координат определяется начальными условиями вывода на орбиту. Начальная точка орбиты и вектор скорости спутника должны лежать в орбитальной плоскости. Для движения спутника по круговой орбите необходимо, чтобы возникающая центробежная сила была равна силе тяготения, или, иначе, чтобы начальная скорость соответствовала круговой скорости Vкр на заданной высоте НА и была направлена перпендикулярно радиус-вектору r.

Для вывода спутника на эллиптическую орбиту необходимо уско­ рить его до второй космической скорости V11= 40300 км/ч = 11, 2 км/с. Скорость движения спутника по эллиптической орбите максимальна в перигее и минимальна в апогее.

При использовании в навигационной системе круговых орбит спутники движутся с постоянной угловой скоростью, что значи­ тельно упрощает расчеты и прогнозирование координат спутников в приемниках потребителей и наземных контрольных станций. С дру­ гой стороны, использование вытянутых эллиптических орбит с апо­ геем, расположенным над заданным районом, позволяет спутнику находиться максимальное время именно над этим районом. Но в этом случае в процессе движения спутника будет значительно из­ меняться расстояние до потребителя и условия прохождения сиг­ нала, что приводит к значительному расширению динамического диапазона и усложнению аппаратуры потребителя. Кроме того, эл­ липтические орбиты менее стабильны. В навигационных системах GPS NAVSTAR и ГЛОНАСС применяются круговые орбиты.