Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Расчет потенциометрических датчиков.

При расчете потенциометрических датчиков применительно к условиям их работы в системах автоматического регулирования обычно требуется определить статическую характеристику и температуру обмотки.

Найдём уравнение статической характеристики U_вых=f(x_вх) для схемы, приведенной на рис. 5.8, в, полагая, что потенциометр является линейным, т.е. все его витки имеют одинаковую длину.

Составим эквивалентную схему (рис. 5.9) и определим общее сопротивление цепи r_э относительно входных зажимов, обозначив полное сопротивление самого потенциометра r₀:

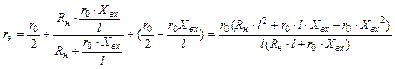
Отсюда общий ток цепи

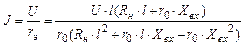(5.15)

а выходное напряжение в предположении, что источник, питающий цепь, обладает нулевым внутренним сопротивлением,

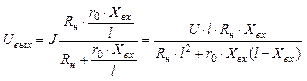(5.16)

Зависимость U_вых=f(X_вх) изображена на рис. 5.10 (кривая 2).

При Х_вх=Х_{вх max}=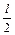

(5.17)

Представив выражение (5.17) в виде

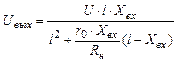
заметим, что при соблюдении условия R_н> > r₀ второй член знаменателя будет значительно меньше первого и им можно пренебречь. В этом случае выражение (5.16) приводится к виду:

(5.18)

и зависимость U^I_вых=f(X_вх) есть прямая, проведенная из начала координат под углом 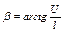(кривая 1). Практически выражение (5.18) дает достаточно точные результаты уже при соотношении R_н> (8…10)r₀

В некоторых случаях, когда вероятные отклонения ползунка в процессе работы системы автоматического регулирования достаточно велики, большую точность может дать линеаризация статистической характеристики методом секущей. Секущая 3 проводится из начала координат в точку А^I с координатами (Х_{вх max} U^I_{вых max}), соответствующую наиболее вероятному максимальному отклонению ползунка. В этом случае

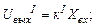
Рис 5.9. Эквивалентная схема потенциометра, включенного по схеме изображенной на рис. 5.8, в.

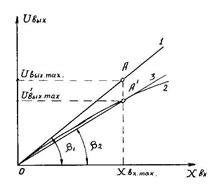
Рис. 5.10. Статистические характеристики линейного потенциометра включенного по схеме, показанной на рис. 5.8, в.

1 – нагруженный потенциометр; 2 – потенциометр с нагрузкой;

3 – линеаризованная характеристика нагруженного потенциометра.

где 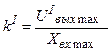(5.19)

Предполагая, что ток нагрузки достаточно мал, а температурный коэффициент сопротивления провода незначителен, перегрев обмотки можно найти из уравнения теплового баланса

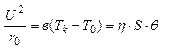(5.20)

где S – площадь поверхности резистора;

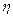- коэффициент теплоотдачи;

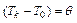- перегрев обмотки;

r₀ – сопротивление обмотки;

в – коэффициент рассеяния.

При выборе допустимой температуры обмотки потенциометра этот вопрос необходимо рассмотреть с двух точек зрения: работы скользящего контакта и возникающих в обмотке механических напряжений.

Желательно, чтобы температура контактных поверхностей не превышала 200⁰ С, так как при более высоких температурах для многих материалов начинается интенсивное окисление.

Надежное контактирование можно обеспечить только в результате правильного выбора натяжения проволоки в процессе намотки. Для этого, помимо конструктивных данных потенциометра, необходимо знать минимально и максимально возможную температуру его обмотки и каркаса.

Для определения конструктивных размеров потенциометра рекомендуется следующая последовательность расчета, которая будет дана для тороидальной конструкции каркаса (см. рис. 5.11), включенного по схеме, приведенной на рис. 5.8, в.

Будем полагать, что заданы:

максимальная величина входного перемещения в одну сторону α _вх.max (рад), чувствительность К; допустимый входной момент М_вх; величина сопротивления нагрузки R_н.

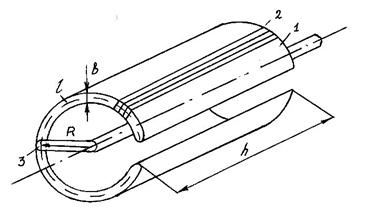
Рис. 5.11. Устройство потенциометра с тороидальным каркасом.

1 – каркас; 2 – обмотки; 3 – ползунок

Предположим, что условие R_н> > r₀ может быть выдержано. Требуемая величина питающего напряжения определяется из выражения:

или с учетом запаса по перемещению (порядка 1, 3…1, 8)

U=3Kα _{вх max} (5.21)

Далее, задавшись материалом обмотки и контактирующей части ползунка, из соотношения

M_вх=RF_n=RFμ (5.22)

можно выбрать радиус потенциометра R и величину контактного давления F.

Здесь μ – коэффициент трения контактирующих поверхностей; F_n – усилие требуемое для перемещения ползунка.

Выбор радиуса потенциометра определяет и длину дуги каркаса (см. рис.5. 10).

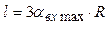(5.23)

Если далее задаться допустимым перегревом обмотки 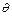, то высота каркаса h и его толщина b определяются выбором диаметра провода обмотки d.

Действительно, учитывая, что в первом приближении

S=2(h+b) ,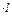

а так же что

(5.24)

где 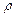- удельное сопротивление;

q – площадь поперечного сечения провода

На основании выражения (20) будем иметь.

Отсюда

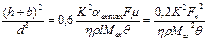(5.25)

Уменьшение диаметра проволоки желательно как с точки зрения уменьшения размеров потенциометра, таки с точки зрения уменьшения ступенчатости статической характеристики (для снижения шумов в системе автоматического регулирования). Однако при этом необходимо ориентироваться на механическую прочность проволоки и, в частности, проверить возникающие в ней напряжения температурного характера.