Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Квазистационарным называют такой ток, для которого время установления одинакового значения по всей цепи значительно меньше периода колебаний.

Будем считать, что для квазистационарных токов, так же как и для постоянных, сила тока одновременно одинакова в любом се­чении неразветвленного проводника. Для них справедлив закон Ома, однако сопротивление цепи зависит от частоты изменения тока. Потерями энергии на электромагнитное излучение этих токов пренебрегаем. Переменный ток можно рассматривать как вы­нужденные электромагнитные колебания.

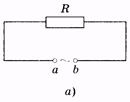
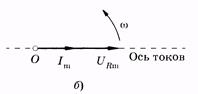
Рис. 14.4

Представим три разных цепи (рис. 14.4, а — 14.6, а), к каждой из которых приложено переменное напряжение

U = U _m cos w t

где U _m— амплитудное значение напряжения, w— круговая частота колебаний.

Для цепи с резистором (рис. 14.4, а) выражение (14.18) запишем в форме

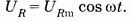(14.19)

Используя закон Ома, получим выражение для тока через сопротивление R:

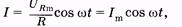(14.20)

где

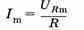(14.21)

— амплитуда тока. Как видно из (14.19) и (14.20), ток и напряжение при этом изменяются в одной фазе, что можно изобразить с помощью векторной диаграммы (рис. 14.4, б). На диаграмме амплитуды U_{R m}и I _т представлены как одинаково направленные векторы, равномерно вращающиеся против часовой стрелки с угловой скоростью w. Проекция этих векторов на «ось токов» (горизонтальная прямая) дает мгновенные значения напряжения и тока. В цепи с сопротивлением Л (омическим сопротивлением) происходит выделение тепла.

Цепь, представленная на рис. 14.5, а, содержит катушку с ин­дуктивностью L, омическое сопротивление равно нулю.

Для этой цепи выражение (14.18) запишем в форме

U_L = U_Lm cos w t. (14.22)

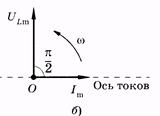
Рис. 14.5

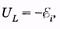
При приложении переменного напряжения U_L в катушке возникает противоположно направленная ЭДС самоиндукции при этом, согласно закону Ома, откуда

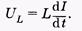(14.23)

Подставляя (14.23) в (14.22), имеем

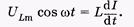(14.24)

Разделив переменные в уравнении (14.24), проинтегрируем его:

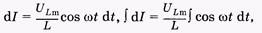
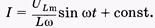(14.25)

Постоянный член в (14.25) равен нулю, так как в цепи действует только переменное напряжение и нет причин для появления постоянной составляющей тока. Окончательно получаем

1 = [ U_{L m} / (L w)]sin w t = 1 _m cos (w t - p/2), (14.26)

где

I _m =U_{L m}(L w) (14.27)

— амплитуда тока. Как видно из (14.26) и (14.22), фаза тока (w t - p/2), а напряжения — w t. Следовательно, ток отстает по фазе от напряжения на p/2, что показано на векторной диаграмме рис. 14.5, б.

Сравнивая (14.27) с законом Ома, заметим, что выражение

Х = L w (14.28)

играет роль сопротивления цепи, которое называют индуктивным. Это сопротивление вместе с U_{L m}определяет силу тока: чем больше частота w и индуктивность L, тем меньше I _m.

При чисто индуктивном сопротивлении теплота в цепи не выделяется, так как R = 0. Роль индуктивности сводится к накоплению энергии магнитного поля и возвращению этой энергии обратно источнику тока. Таким образом, происходит периодическая перекачка энергии от источника в цепь и от цепи к источнику, в идеальном случае без потерь энергии.

В цепи, в которой имеется только конденсатор с электроемкостью С (рис. 14.6 а), омическое сопротивление всюду, кроме емкости, и индуктивность цепи равны нулю. Омическое сопротивление R конденсатора для постоянного тока бесконечно велико. Напряжение на конденсаторе выражается зависимостью:

U_С = U_{C m}cos w t. (14.29)

Ток в цепи будет определяться скоростью изменения заряда на обкладках конденсатора. Используя соотношение для электроемкости, найдем

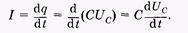(14.30)

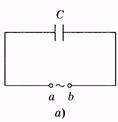
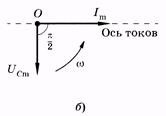
Рис. 14.6

На основании (14.29) запишем

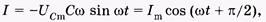(14.31)

где

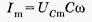(14.32)

— амплитуда тока. Как видно из (14.31) и (14.29), фаза тока (w t - p/2), а напряжения — w t. Следовательно, ток опережает напряжение на p/2, что показано на векторной диаграмме (рис. 14.6, б).

Сравнивая (14.32) с законом Ома, заметим, что выражение

Х_L = L w (14.33)

играет роль сопротивления цепи, которое называют емкостным. Оно определяет амплитуду тока: чем меньше емкость С и частота со, тем меньше I _m. Для постоянного тока (w = 0) емкость является бесконечно большим сопротивлением, и тока в такой цепи не будет. Заметим, что отсутствие конденсатора в цепях с резистором или индуктивностью формально означало не С = 0, а Х_C = 0, т. е. С ® ¥.

В цепи с конденсатором теплота не выделяется, так как омическое сопротивление проводников равно нулю (нагревание диэлектрика в переменном электрическом поле здесь не учитывает­ся, оно будет рассмотрено позже). Роль емкости сводится к накоплению энергии электрического поля конденсатора и возвращению этой энергии обратно источнику тока. Происходит периодическая перекачка энергии от источника в цепь и от цепи к источнику, в идеальном случае без потерь энергии.

Из формул (14.28) и (14.33) можно убедиться, что индуктивное и емкостное сопротивление в СИ измеряются в омах.