
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В-пятых, это так называемая дисперсия остатков.
|
|
Этот показатель рассчитывается по формуле:
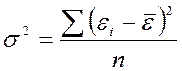 , где
, где
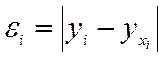 - так называемые «остатки» уравнений регрессии, т.е. отклонения теоретических (расчетных) значений переменной y от ее фактических значений.
- так называемые «остатки» уравнений регрессии, т.е. отклонения теоретических (расчетных) значений переменной y от ее фактических значений.
Наконец, это так называемый критерий Фишера, который позволяет оценить статистическую значимость самого индекса детерминации. Критерий Фишера рассчитывается по формуле:
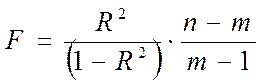
где n - число наблюдений (то есть известных значений всех переменных) или, что то же самое, длина ряда исходных статистических данных;
m – число параметров уравнения регрессии.
Число параметров, как правило, на единицу больше числа переменных (хотя из этого общего правила могут быть исключения).
Например, в уравнении двухфакторной линейной регрессии 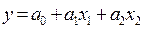 три параметра:
три параметра: 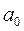 ,
, 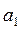 ,
, 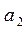 , то есть
, то есть 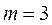
Расчетное значение 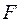 сравнивается с табличным при количестве степеней свободы:
сравнивается с табличным при количестве степеней свободы: 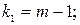
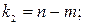
Наконец, имеется еще такой специальный показатель, как критерий Стьюдента, который используется не для оценки значимости всего уравнения в целом, а отдельных параметров уравнения регрессии. Критерий Стьюдента может использоваться в качестве дополнительного критерия отбора факторов, которые целесообразно включить в модель регрессии. Значимость отдельного параметра уравнения регрессии характеризует то, насколько случайным является отличие данного параметра от нуля.
Таким образом, если оказалось, что параметр 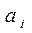 при переменной
при переменной  не является значимым, то это значит, что фактор
не является значимым, то это значит, что фактор  не играет важной роли, и целесообразно исключить его из уравнения, то есть построить новое уравнение регрессии без этого фактора.
не играет важной роли, и целесообразно исключить его из уравнения, то есть построить новое уравнение регрессии без этого фактора.
Обычно в уравнении множественной линейной регрессии значения критерия Стьюдента рассчитываются по формулам:
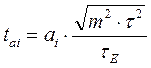 ,
, 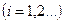 для любого параметра, кроме a0, а для параметра a0 этот критерий определяется по формуле:
для любого параметра, кроме a0, а для параметра a0 этот критерий определяется по формуле:
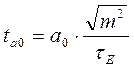
Расчетное значение критерия Стьюдента (так же, как и значение критерия Фишера) сравнивается с табличным. Если расчетное значение превышает табличное, то данный параметр считается значимым.
Далее мы остановимся на содержательном смысле критерия Фишера и критерия Стьюдента более подробно.
2й учебный вопрос: Общие правила проверки статистических гипотез.
Обычно в выборочных наблюдениях, как известно из курса теории статистики, оценку генерального параметра получают на основе выборочного показателя с учетом ошибки репрезентативности. Ошибка выборки – это разница между значениями показателя, полученного по выборке и генеральным параметром. В другом случае в отношении свойств генеральной совокупности выдвигается некоторая гипотеза о величине средней, дисперсии, характере распределения, форме и тесноте связи между переменными. Проверка гипотезы осуществляется на основе выявления согласованности эмпирических данных с гипотетическими (теоретическими). Если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных. Основой проверки статистических гипотез являются данные случайных выборок. При этом безразлично, оцениваются ли гипотезы в отношении реальной или гипотетической генеральной совокупности. Последнее открывает путь применения этого метода за пределами собственно выборки: при анализе результатов эксперимента данных сплошного наблюдения, но малой численности. В этом случае рекомендуется проверить, не вызвана ли установленная закономерность стечением случайных обстоятельств, насколько она характерна для того комплекса условий, в которых находится изучаемая совокупность.
Статистической гипотезой (обозначается Н) называется предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки. Так, может быть выдвинута гипотеза о том, что средняя 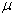 в генеральной совокупности равна некоторой величине а (записывается Н:
в генеральной совокупности равна некоторой величине а (записывается Н: 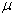 = а) или о том, что генеральная средняя больше некоторой величины (Н:
= а) или о том, что генеральная средняя больше некоторой величины (Н: 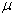 > в).
> в).
Различают простые и сложные гипотезы. Гипотеза называется простой, если она однозначно характеризуется параметром распределения случайной величины. Например, Н: 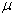 = а.
= а.
Сложная гипотеза состоит из конечного или бесконечного числа простых гипотез, при этом указывается некоторая область вероятных значений параметра. Например, Н: 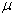 > в. Эта гипотеза состоит из множества простых гипотез Н:
> в. Эта гипотеза состоит из множества простых гипотез Н: 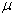 = с, где с – любое число, большее в.
= с, где с – любое число, большее в.
Гипотезы о параметрах генеральной совокупности называются параметрическими, о распределениях – непараметрическими. Гипотеза о том что две совокупности сравниваемые по одному или нескольким признакам, не отличаются, называется нулевой гипотезой или нуль-гипотезой (обозначается Н0). При этом предполагается, что действительное различие сравниваемых величин равно нулю, а выявленное по данным отличие от нуля носит случайный характер. Например, Н0: 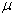 1 =
1 = 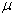 2 и т.д.
2 и т.д.
Нулевая гипотеза отвергается тогда, когда по выборке получается результат, который при истинности выдвинутой нулевой гипотезы маловероятен. Границей невозможного или маловероятного обычно считают  = 0, 05, т.е. 5% или 0, 01, 0, 001. Если ориентироваться на правило «трех сигм» (оно состоит в следующем:
= 0, 05, т.е. 5% или 0, 01, 0, 001. Если ориентироваться на правило «трех сигм» (оно состоит в следующем: 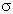 = 1/6(хmах - хmin), так как в нормальном распределении в размахе вариации «укладывается» 6
= 1/6(хmах - хmin), так как в нормальном распределении в размахе вариации «укладывается» 6 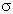 (±3
(±3 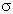 )), то вероятность ошибки a должна быть равна 0, 0027. Однако для этого уровня вероятности ошибки значений критериев редко табулируются: как правило, значения критериев в статистико-математических таблицах рассчитаны для вероятностей ошибки 0, 05; 0, 01; 0, 001.
)), то вероятность ошибки a должна быть равна 0, 0027. Однако для этого уровня вероятности ошибки значений критериев редко табулируются: как правило, значения критериев в статистико-математических таблицах рассчитаны для вероятностей ошибки 0, 05; 0, 01; 0, 001.
Статистическим критерием называют определенное правило, устанавливающее условия отклонения проверяемой нулевой гипотезы. Проверка статистических гипотез состоит из следующих этапов:
· формулируется в виде статистической гипотезы задача исследования;
· выбирается статистическая характеристика гипотезы;
· выбираются испытуемая и альтернативная гипотезы на основе анализа возможных ошибочных явлений и их последствий;
· определяется область допустимых значений, критическая область, а также критическое значение статистического критерия (t; F; 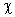 2) по соответствующей таблице;
2) по соответствующей таблице;
· вычисляется фактическое значение статистического критерия;
· проверяется гипотеза на основе сравнения фактического и критического значений критерия, и в зависимости от результатов проверки гипотеза либо отклоняется, либо не отклоняется.
При проверке гипотез по одному из критериев возможны 2 ошибочных решения:
- неправильное отклонение Н0: ошибка 1-го рода;
- неправильное принятие Н0: ошибка 2-го рода.
В то время, как фактически Н0 верна (1) и Н0 не верна (2), принимают 2 ошибочных решения:
- Н0 отклоняется и принимается альтернативная гипотеза;
- Н0 не отклоняется
Вероятности, соответствующие неверным решениям, называется риском 1 и риском 2. Риск 1 равен вероятности ошибки α (уровню значимости), риск 2 равен вероятности ошибки β. Поскольку α всегда больше 0, то всегда есть риск ошибки β. Обычно задают значение α и пытаются сделать возможно β малым. Вероятность 1-β называется мощностью критерия: чем она больше, тем меньше вероятность ошибки 2-го рода.
Альтернативная гипотеза Н1 может быть сформулирована по-разному в зависимости от того, какие отклонения от гипотетической величины нас особенно беспокоят: положительные, отрицательные либо и те, и другие. Соответственно альтернативные гипотезы могут быть записаны как:
Н1: 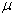 > а, Н1:
> а, Н1: 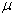 < а, Н1:
< а, Н1: 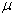
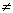 а
а
3й учебный вопрос: Оценка значимости уравнений регрессии с помощью критерия Фишера.
После построения уравнения линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, следовательно, фактор х не оказывает влияния на результат у.
Величина F–отношения (F-критерий) получается при сопоставлении факторной и остаточной дисперсии в расчете на одну степень свободы.
F = Dфакт / Dост (5.5)
F-критерий проверки для нулевой гипотезы Н0: Dфакт = Dост
Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным (отличным от 1), если оно больше табличного.
В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл Н0 отклоняется.
Если же величина оказалась меньше табличной Fфакт < Fтабл, то вероятность нулевой гипотезы меньше заданного уровня (например, 0, 05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым и не отклоняется. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. В математической статистике дисперсионный анализ рассмотрен как самостоятельный инструмент (метод) статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества модели. Центральное место в анализе дисперсии занимает разложение общей суммы квадратов отклонений переменной у от среднего значения у на 2 части - «объясненную» и «необъясненную»:
| Общая сумма квадратов отклонений | = | Сумма квадратов отклонений, объясненная регрессией | + | Остаточная сумма квадратов отклонений |
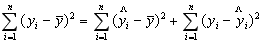 (5.6)
(5.6)
или Q = Q R + Q e (5.7)
В переводной литературе обычно принято следующее обозначение:
TSS = RSS + ESS
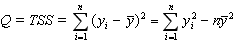 - общая сумма квадратов отклонений; (5.8)
- общая сумма квадратов отклонений; (5.8)
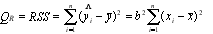 – сумма квадратов отклонений, обусловленная регрессией; (5.9)
– сумма квадратов отклонений, обусловленная регрессией; (5.9)
Q = ESS = 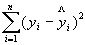 – остаточная сумма квадратов отклонений. (5. 10)
– остаточная сумма квадратов отклонений. (5. 10)
Таблица 5.1
|
|