
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Графический метод
|
|
О величине перекрытия судят по коэффициенту перекрытия, который выражают отношением угла торцового перекрытия к угловому шагу. Угол торцового зацепления a – это угол поворота колеса от положения зубьев при входе в зацепление. Следовательно, Е = jа1/t1, где t1=2p/z1– угловой шаг.

Если Е< 1, то непрерывности зацепления зубьев не будет.
Виды смещений. Основной вид смещения при нарезании, уравнительное и воспринимаемое смещения.
1) смещение равно 0

2) Начальная прямая, которая катится без скольжения в процессе нарезания зубчатых колес Хm> 1 Þ это случай положительного смещения.

3) Xm< 0 – случай отрицательного смещения.
начальная прямая

xΣ – суммарный коэф-т смещения x1+x2=xΣ , y – коэф-т воспринимаемого смещения, Δ y – коэф-т уравнительного смещения. Δ y= xΣ –y
Передаточное отношение одно- и многоступенчатых зубчатых
передач с неподвижными
осями вращения.
Одноступенчатая передача с внешним зацеплением. Особенность: меняет знаки. u12=±ω 1/ω 2, ω 1=vk/r1, ω 2=vk/r2.
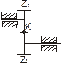
Одноступенчатая зубчатая передача с внутренним зацеплением. Особенность: не меняет знаки.
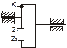
Подставим ω 1 и ω 2 в формулу для передаточного отношения u12:
u12=±r2/r1=±z2/z1.
Многоступенчатая зубчатая передача с неподвижными осями (односторонние зубчатые передачи соединены последовательно:

u16 = u12 ∙ u34 ∙ u56 =
= (-1)ω 1/ω 2 ∙ ω 3/ω 4 ∙ (-1)ω 5/ω 6 =
= ω 1/ω 2 ∙ ω 3/ω 4 ∙ ω 5/ω 6 =
= (-1) z2/z1 ∙ z4/z3 ∙ (-1) z6/z5
Передаточное отношение многоступенчатой зубчатой передачи = передаточному отношению входному колесу от выходного колеса.
z2∙ z4∙ z6 - произведение числа зубьев ведомых колес.
z1∙ z3∙ z5 - произведение числа зубьев ведущих колес. Тогда Uвх/вых = Пzведомых колес/Пzведущих колес × (-1)k, где k – число внешних зацеплений.
Определение передаточного отношения планетарного механизма аналитическим методом (методом обращения движения).
Если одно из центральных колес многоступенчатого зубчатого механизма неподвижно, то она называется планетарным механизмом.
Число степеней свободы W=3n-2p1-
-2p2=3∙ 3-2∙ 3-2=1
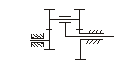
Планетарный механизм, имеющий неподвижное звено всегда можно превратить в дифференциал, и наоборот. Это и есть свойство обратимости планетарных механизмов. Основная идея метода Виллиса (метода обращения движения): берем центральное звено планетарного механизма и даем ему дополнительное вращение равное скорости вращения водила, но направленное в противоположную сторону. Тогда водило становится неподвижным звеном и механизм из планетарного превращается в зубчатый механизм с неподвижными осями колес (обращенный механизм), состоящий из нескольких последовательных соединенных пар зубчатых колес.
| Движение | Z1 | в | Z4 |
| действит. | Ω 1 | ω в | |
| Дополнит | -ω в | -ω в | -ω в |
| суммарное | ω 1-ω в | -ω в |
Передаточное отношение обращенного механизма имеет вид:
u14(в)=(ω 1-ω в)/(-ω в)=(-1)2z2z4/z1z3
u1в(4)=ω 1/ω в=1-u14(в)
u1в - передаточное отношение планетарного механизма.
uв1(4)=1/u1в(4)=1/1-u14(в)
Передаточное отношение от четвертого колеса к водилу, если первое колесо остановлено: u4в(1)=1-u41(в)
uв4(1)=1/u4в(1)=1/1-u41(в)
u1в(4)=1/1-u14(в)=1-z2z4/z1z3=
1-99∙ 101/100∙ 100=0, 0001
uв1(4)=1/u1в(4)=10000
Т.е. при одном обороте водила колесо повернется на 0, 0001.
Передаточное отношение планетарного механизма по методу баланса мощностей в балансу моментов.
u1в -?
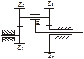
u1в=1-u14(в)=1-(-1)2z2z4/z1z3=1-r2r4/r1r3
⌠ M1ω 1+Mвω в=0
│ M1+Mв+M4=0
ω 1/ω в=-Mв/M1=(M1+M4)/M1=1+M4/M1
M1=F12∙ r1, M4= -F43∙ r4, F34∙ r3=F21∙ r2,
F34= F21∙ r2/r3, F43= -F34= -F21∙ r2/r3,
M4= -F43∙ r4= F21∙ r2r4/r3,
u1в=ω 1/ω в=1+M4/M1=
=1-F12∙ r2∙ r4/F12∙ r1∙ r3=1-r2r4/r1r3
Передаточное отношение планетарных механизмов графическим методом.
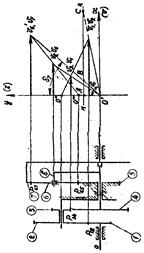
Особенности определения передаточного отношения дифференциальных механизмов с замыкающей кинематической цепью аналитическим и графическим методами.
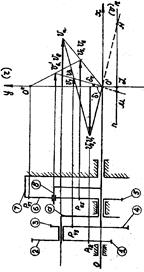
Механизм имеет два водила «a», «в» Þ содержит 2 планетарных механизма. Т.к. оба центральных колеса могут вращаться, заключаем, что левая часть заданного механизма, состоящая из водила «а», сателлита 2-3 и центральных колес 1, 4 является дифференциалом (два колеса могут вращаться). Данный механизм является замкнутым, т.к. в выделенном дифференциале водило «а» и колесо 4 соединены между собой зубчатой передачей. Замыкающая цепь содержит водило «в», на котором установлен сателлит. Поскольку центральное колесо 7 здесь неподвижно, то замыкающая цепь (колеса 5 и 7, водило «в» и сателлит 6) представляет собой простой планетарный механизм. Рассмотрим дифференциал (1, 2-3, «а», 4) отдельно. Воспользуемся методом Виллиса, т.е. остановим водило, преобразуем дифференциал в приведенный зубчатый механизм.
| Движение | а | ||
| действит. | ω а | w1 | w4 |
| дополнит. | -ω а | -ω а | -ω а |
| суммарное | w1(а)= =w1–wа | ω 4(а)= =w4–wа |
Далее, для приведенного механизма составляем отношение угловых скоростей центральных колес и выражаем его через радиусы: i14(a)=w1(a)/w4(a)=(w1–wa)/(w4–wa)=(r2r4)/(r1r3)
После этого рассматриваем отдельно замыкающую цепь. Поскольку она выполнена в виде простого планетарного механизма, то и здесь применяем метод Виллиса:
| Движение | в | ||
| действит. | ω в | w5 | w7 =0 |
| дополнит | -ω в | -ω в | -ω в |
| суммарное | w5(в)= w5–wв | ω 7(в)= –wв |
i57=w5(в)/w7(в)=(w5–wв)/(–wв) = –r7/r5. С целью определения искомого передаточного отношения решаем полученные уравнения совместно:
(1-е): (w1–w5)/(w4–w5) = r2r4/(r1r3),
(2-е): 1–w5/w4= –r7/r5.
Из 2-го уравнения w5=w4(1+r7/r5). Подставив это значение в 1-е уравнение, получим: [w1–w4(1+r7/r5)] /
/ [w4–w4(1+r7/r5) = (r2r4)/(r1r3), сократив на w4, получим: [(w1/w4) – (1+r5/r7)] /
/ [1–(1+r7/r5)]=r2r4/(r1r3). Отсюда i14=w1/w4=1+r7/r5–(r2r4r7)/(r1r3r5).
Дифференциал автомобиля и его кинематика.

(ω 1-ω в)/(ω 4-ω в)=1, ω 1-ω в= - (ω 4-ω в)
(ω 1+ω 4)/ω 2=ω в
Имитация движения автомобиля на повороте:
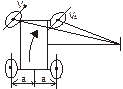
Ω =vЛ/(R+a)= vП/(R–a)
ω Л/(R+a)=ω П/(R–a)
ω Л/ω П=(R+a)/R–a)
Кулачковые механизмы. Назначение и виды кулачковых механизмов.
Кулачковые механизмы преобразуют вращательное движение начального звена (кулачка) в возвратно-поступательное движение выходного звена (толкателя). При этом форма кулачка определяет закон движения толкателя. Кулачковые механизмы бывают следующих видов:
1) Плоский кулачок с качающимся толкателем. 1-кулачок, 2-толкатель, 3-ролик, 4-силовой элемент (пружина).
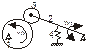
2) Плоский кулачок с поступательно перемещающимся толкателем.
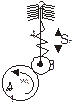
3) Пространственный кулачок.
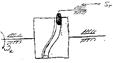
Основные этапы проектирования кулачкового механизма.
1)Выбор схемы кулачкового механизма, 2)Определение закона движения толкателя, 3)Выбор основных размеров кулачкового механизма, 4)Профилирование кулачка.
vT=ST¢ ∙ ω K, где S¢ T – аналог скорости толкателя, dS/dφ k, aT≈ ST¢ ¢ ∙ ω K2, aT=ST¢ ¢ ∙ ω K+ST¢ ∙ EK, ST¢ ¢ =d ST¢ /dφ k≈
≈ ∆ ST¢ /∆ φ = ST¢ /∆ φ при Δ φ → 0, ST¢ ¢ → ∞, что соответствует жесткому удару (скачкообразно изменяется аналог скорости толкателя ST¢)

jП – фаза подъема толкателя. 1– жесткий удар, 2–мягкий удар (скорость толкателя нарастает быстрее), 3, 4, 5– безударное движение.
Графические методы определения закона движения толкателя.
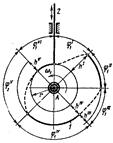
Схема механизмам поступательно движущимся толкателем
 Закон движения ведомого звена
Закон движения ведомого звена
(толкателя)
Определение минимальных размеров кулачка.
Режим самозаклинивания толкателя – когда толкатель не может передвигаться. r0 – минимальный радиус. Для кулачков с поступательным движением толкателя угол давления (α) не более 300. Для кулачков с качающимся толкателем угол давления (α) допускается до 450.

По основной теореме зацепления: wK/wT=KOT/OKK = ℓ T/DB (по подобию треугольников), DB = ℓ TwT/wK, S¢ × wK = VT. tgq=DN/NOK = [(ℓ T+ST¢)–a× cosjT]/[a× sinj], q–угол зацепления.
a× sinjT × tgq + a× cosjT = (ℓ T+ST¢), a=(ℓ T+ST¢)/ (sinjT × tgq + cosjT)
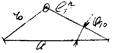
r0 = Ö (a2+ℓ T2–2aℓ TcosjT0)
Определение действительного профиля кулачка.
⌠ xB=a-eTcosφ T(φ K)
│ yB=eTsinφ T(φ K)
(x-xB)2+(y-yB)2=r2
-2(x-xB)∙ dxB/dφ K–2(y-yB)∙ dyB/dφ K=0
(x-xB)= -(y-yB)(dyB/dφ K)/(dxB/dφ K)
(y-yB)2 ∙ [(dyB/dφ K)/(dxB/dφ K)]2+(y-yB)2=r2,
(y – yB)2 = r2 × (dxB/djK)2 / [(dxB/djK)2 + (dyB/djK)2], y = yB ± r × (dxB/djK) / Ö [(dxB/djK)2 + (dyB/djK)2]
x = xB ± r × (dyB/djK) / Ö [(dxB/djK)2 + (dyB/djK)2]
|
|
