
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение теплового баланса непроточного водоема
|
|
Основу методики теплового расчета водоемов составляет уравнение теплового баланса водоема.
Впервые метод теплового баланса был применен в 1920-х годах исследователем Л.Ф.Рудовицем при оценке интенсивности испарения с Каспийского моря. В эти же годы В.В.Шулейкин на основе составления теплового баланса установил наличие теплого течения из Баренцева моря в Карское море. Тогда же этот прогноз был блестяще подтвержден специальными экспедиционными исследованиями. В 1929г. Н.М.Бернадский разработал методику расчета прудов-холодильников (проточных водоемов), которые начали создаваться в первой пятилетке по плану ГОЭЛРО в большом количестве при строительстве тепловых электростанций. Эта методика основана на методе теплового баланса и почти в неизменном виде используется до сих пор при гидротехническом проектировании.
Рассмотрим тепловой баланс водоемов. Для этого воспользуемся дифференциальным уравнением теплопроводности (5.9). Уравнение (5.9) описывает самый общий случай температурного поля — нестационарного, пространственного. Решить это уравнение аналитически чрезвычайно трудно. Поэтому рассмотрим только частные случаи теплового баланса водоемов.
Тепловой баланс непроточного водоема. Для непроточного водоема (υ x = υ y = υ z = 0) уравнение (5.9) примет следующий вид:
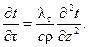 (5.15)
(5.15)
При переходе от уравнения (5.9) к уравнению (5.15) предполагалось, Что температурный режим водоема вдоль координат х и у не меняется (∂ 2 t/∂ x 2 = 0, ∂ 2 t/∂ y 2 = 0). Это справедливо, если глубина водоема и граничные условия вдоль этих координат не меняются.
После интегрирования уравнения (5.15) по глубине водоема получим
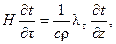 (5.16)
(5.16)
или

(5.17)
Левая часть уравнения (5.17) представляет собой изменение энтальпии отсека водоема площадью 1 м2 и глубиной H. Оно обусловлено тепловыми потоками, поступающими в этот отсек через поверхность и дно. Следовательно, правую часть уравнения (5.17) можем заменить суммой тепловых потоков через эти поверхности:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
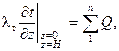 (5.18)
(5.18)
где 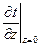 и
и 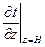 — температурный градиент у поверхности воды и у дна,
— температурный градиент у поверхности воды и у дна,
п — число слагаемых потоков.
Решая совместно уравнения (5.17) и (5.18), получаем
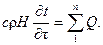 (5.19)
(5.19)
Таким образом, изменение средней температуры воды непроточного водоема во времени (∂ t/∂ τ) определяется граничными условиями (второго и третьего рода) — суммой тепловых потоков через его поверхности.
|
|
