
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Коефіцієнти кореляції та детермінації
|
|
Побудова рівняння регресії дає нам можливість розкласти значення уі в кожному спостереженні на дві складові:
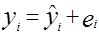 . (1.11)
. (1.11)
Величина 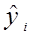 – розраховане за оціночним рівнянням економетричної моделі значення результативного показника в і -му випадку. Залишок е і є розбіжністю між фактичним і прогнозним значенням змінної у, тобто, та частина у, яку ми не можемо пояснити з допомогою рівняння регресії. Знайдемо
– розраховане за оціночним рівнянням економетричної моделі значення результативного показника в і -му випадку. Залишок е і є розбіжністю між фактичним і прогнозним значенням змінної у, тобто, та частина у, яку ми не можемо пояснити з допомогою рівняння регресії. Знайдемо
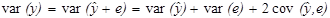 . (1.12)
. (1.12)
Врахувавши, що 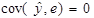 , будемо мати:
, будемо мати:
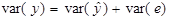 . (1.13)
. (1.13)
Дане співвідношення означає, що ми можемо розкласти загальну дисперсію var(y) на дві складові: 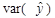 – частина, яка пояснює рівняння регресії (пояснююча дисперсія) і var(e) – непояснююча частина (дисперсія помилок або не пояснююча дисперсія).
– частина, яка пояснює рівняння регресії (пояснююча дисперсія) і var(e) – непояснююча частина (дисперсія помилок або не пояснююча дисперсія).
У лівій частині (1.13) маємо варіацію залежної змінної у навколо свого вибіркового середнього значення 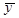 , а у правій – варіації розрахункових значень
, а у правій – варіації розрахункових значень 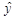 навколо середнього значення
навколо середнього значення 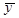 та фактичних значень у. За означенням дисперсії (1.13) прийме наступний вид:
та фактичних значень у. За означенням дисперсії (1.13) прийме наступний вид:
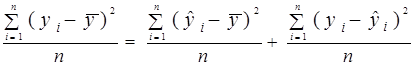 ,
,
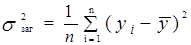 – загальна дисперсія; (1.14)
– загальна дисперсія; (1.14)
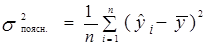 – пояснююча дисперсія; (1.15)
– пояснююча дисперсія; (1.15)
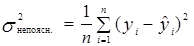 – дисперсія помилок, або (1.16)
– дисперсія помилок, або (1.16)
непояснююча дисперсія.
Тобто, з (1.14) маємо: 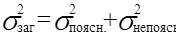 .
.
Якщо загальну дисперсію вважати незмінною, то чим більша буде пояснююча дисперсія, тим менша непояснююча, а значить менший розкид точок на діаграмі розсіювання відносно оціночної прямої.
Далі поділимо обидві частини (1.13) на var (y) і отримаємо:
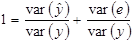 (1.17)
(1.17)
Як можна побачити з виразу (1.17) перша частина 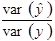 є складовою дисперсії, яку можна пояснити через лінію регресії. Друга частина
є складовою дисперсії, яку можна пояснити через лінію регресії. Друга частина 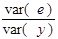 є пропорцією дисперсії помилок у загальній дисперсії, тобто являє собою частину дисперсії, яку не можна пояснити через регресійний зв’язок.
є пропорцією дисперсії помилок у загальній дисперсії, тобто являє собою частину дисперсії, яку не можна пояснити через регресійний зв’язок.
Частина дисперсії, що пояснюється регресією, називається коефіцієнтом детермінації і позначається d або r 2:
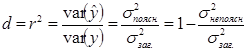 (1.18)
(1.18)
З цієї формули видно, що коефіцієнт детермінації завжди додатній і знаходиться в межах від нуля до одиниці. Максимальне значення d =1, за умови, що лінія регресії точно відповідає всім спостереженням (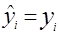 і всі залишки рівні нулю). Тоді
і всі залишки рівні нулю). Тоді 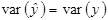 . Якщо ж для вибірки відсутній зв’язок між змінними у та х, то коефіцієнт d буде близький до нуля.
. Якщо ж для вибірки відсутній зв’язок між змінними у та х, то коефіцієнт d буде близький до нуля.
Після побудови регресійної моделі необхідно оцінити тісноту зв’язку між результативною та факторною змінними. Для цього необхідно розрахувати коефіцієнт кореляції, який саме характеризує ступінь щільності лінійної залежності між випадковими величинами х та у. Він позначається r і розраховується за формулою:
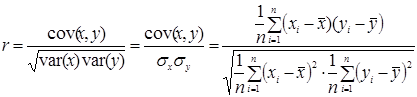 ,
,
де cov(x, y) – коефіцієнт коваріації між змінними х та у, var(x), var(y) – дисперсії змінних х та у, а sx, sy – їх середні квадратичні відхилення.
Коефіцієнт кореляції, на відміну від коефіцієнта коваріації, є вже не абсолютною, а відносною мірою зв’язку між двома факторами і приймає значення з інтервалу [-1; 1]. Додатне значення кореляції свідчить про наявність прямого зв’язку між змінними, а від’ємне – про зворотній зв’язок. Якщо коефіцієнт кореляції прямує до ±1, то мова йде про наявність тісного лінійного зв’язку між змінними. У той же час, коли він прямує до нуля, то лінійний зв’язок між змінними слабкий. Але, якщо нами отримано r =0, то не треба спішити з висновками про відсутність зв’язку між змінними. Можна лише робити висновок про відсутність лінійного зв’язку, але між вибраними змінними може існувати тісний нелінійний зв’язок. Коефіцієнт кореляції дає можливість робити висновок про тісноту саме лінійного зв’язку між змінними.
Подивимось, чи існує зв’язок між коефіцієнтом детермінації і коефіцієнтом кореляції. Для цього здійснимо наступні перетворення для коефіцієнта детермінації:
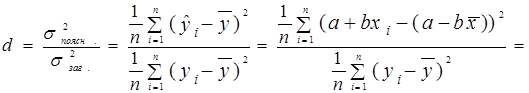
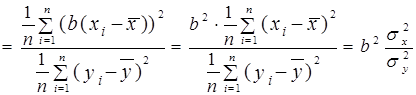 .
.
Виконаємо аналогічні перетворення для коефіцієнта кореляції, врахувавши, що 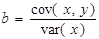 :
:
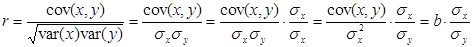 .
.
З останньої формули видно, що знак коефіцієнта кореляції визначається знаком оцінки b.
Ми бачимо, що коефіцієнт кореляції є коренем квадратним з коефіцієнта детермінації:
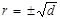 . (1.19)
. (1.19)
Приклад 1.2. На основі даних прикладу 1.1 потрібно:
1. Обчислити загальну, пояснюючу та непояснюючу дисперсію.
2. Знайти значення коефіцієнтів детермінації та кореляції.
¨ Розв’язування.
1. Для знаходження дисперсій використаємо наступні формули:
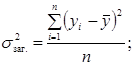
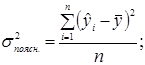
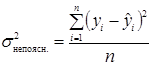 .
.
Для спрощення підрахунків побудуємо таблицю, взявши середні значення змінних з прикладу 1.1:

| № п/п | yi | xi | 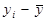
| 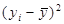
| 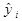
| 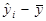
| 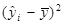
| 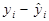
| 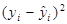
|
| 1 | 2, 2 | 1, 4 | -5, 07 | 25, 7 | 3, 74 | -3, 53 | 12, 49 | -1, 54 | 2, 36 |
| 2 | 4, 2 | 2, 2 | -3, 07 | 9, 42 | 4, 64 | -2, 63 | 6, 91 | -0, 44 | 0, 2 |
| 3 | 5, 7 | 3, 3 | -1, 57 | 2, 46 | 5, 89 | -1, 38 | 1, 91 | -0, 19 | 0, 04 |
| 4 | 6, 8 | 2, 6 | -0, 47 | 0, 22 | 5, 09 | -2, 18 | 4, 73 | 1, 71 | 2, 91 |
| 5 | 5, 9 | 3, 2 | -1, 37 | 1, 88 | 5, 77 | -1, 50 | 2, 24 | 0, 13 | 0, 02 |
| 6 | 7, 6 | 4, 5 | 0, 33 | 0, 11 | 7, 25 | -0, 02 | 0, 35 | 0, 12 | |
| 7 | 9, 5 | 5, 1 | 2, 23 | 4, 97 | 7, 93 | 0, 66 | 0, 43 | 1, 57 | 2, 47 |
| 8 | 8, 4 | 6, 7 | 1, 13 | 1, 28 | 9, 74 | 2, 47 | 6, 1 | -1, 34 | 1, 79 |
| 9 | 10, 1 | 7, 3 | 2, 83 | 8, 01 | 10, 42 | 3, 15 | 9, 92 | -0, 32 | 0, 1 |
| 10 | 12, 3 | 8, 9 | 5, 03 | 25, 3 | 12, 23 | 4, 96 | 24, 62 | 0, 07 | |
| Сума | 72, 7 | 45, 2 | 79, 36 | 72, 7 | 69, 35 | 10, 01 |
Отже, маємо:
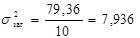 ;
; 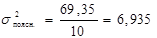 ;
; 
2. Знайдемо значень коефіцієнтів детермінації та кореляції.
Для обчислення коефіцієнта детермінації використовуємо формулу:
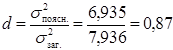 ,
,
а це означає, що 87 % загальної дисперсії пояснюється оціночною прямою, на долю неврахованих факторів припадає 13 %.
Коефіцієнт кореляції знайдемо за формулою:
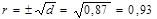 .
.
Знак коефіцієнта кореляції визначається знаком кутового коефіцієнта оціночного рівняння b (в нашому випадку він додатний). Отримане значення коефіцієнта кореляції вказує на ступінь тісноти лінійного зв’язку між змінними. Значення коефіцієнта кореляції рівне 0, 93 (близьке до одиниці), а це значить, що лінійна форма зв’язку між змінними у та х вибрана вірно і цей зв’язок тісний.
|
|