
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неньютоновские жидкости.
|
|
Течение некоторых жидкостей (коллоидных растворов, нефтей с большим содержанием асфальтенов и парафинов, растворы полимеров и т.д.) не подчиняются закону Ньютону. Такие жидкости в реологии принято называть неньютоновскими или аномальными.
Закон Ньютона обычно нарушается при течении коллоидных растворов с удлиненными частицами дисперсной фазы, способными деформироваться в поле напряжений и структурированных систем. Такие коллоидные системы обладают определенными механическими свойствами – пластичностью, упругостью, прочностью и вязкостью. Эти свойства в большинстве случаев связаны с образованием структуры в жидкости, и поэтому их часто называют структурно-механическими или реологическими свойствами.
Основы реологии коллоидных растворов впервые изучены Ф.Н.Шведовым, Бингамом и Грином. В 1889 году Ф.Н. Шведов, позже в 1916 году Бингам установили, что течение системы с пространственной структурой начинается лишь тогда, когда напряжение сдвига τ превышает определенное критическое значение τ 0, необходимое для разрушения в жидкости структурной сетки. Такое течение было названо пластическим, а критическое напряжение сдвига – пределом текучести или предельным напряжением сдвига.
Систему, течение которой подчиняется такой идеализированной схеме, в реологии называют телом Бингама или бингамовскими пластиками. Они описываются следующим реологическим уравнением Бингама-Шведова:
| τ – τ 0 = μ ’ | du | (2) |
| dx |
где μ ’ – пластическая вязкость системы.
Для ньютоновских жидкостей предельное напряжение сдвига равно нулю, и уравнение (2) переходит в закон Ньютона, а пластическая вязкость – в истинную вязкость. Из уравнения (2) следует: система до τ 0 упруго деформируется, после этого течет с постоянной пластической вязкостью μ ’ = (τ –τ 0) / (du/dx).
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
В области упругой деформации вязкость бингамовского пластика чрезвычайно высокая. Здесь упруго деформируется структурный «каркас» из частиц дисперсной фазы. При превышении τ 0, согласно уравнению Бинагама-Шведова, структурная сетка мгновенно разрушается, и вязкость системы принимает постоянное значение.
Линия консистентности бингамова тела выражается прямой линией, отсекающей отрезок на оси абсцисс, равный τ 0 от начала координат (рис.1).
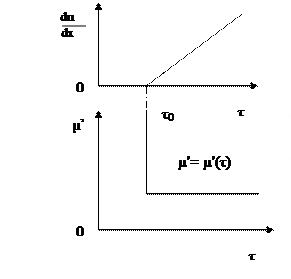
Рис.1. Линия консистентности и зависимость μ ’ от τ для пластической жидкости.
Примером систем, хорошо подчиняющихся уравнению (2), могут служить нефти с высоким содержанием парафинов при температурах ниже температуры кристаллизации. Однако у многих реальных структурированных коллоидных систем линия консистентности оказывается не прямой, а кривой, отсекающей на оси напряжений сдвига некоторый отрезок (рис.2). В этом случае при достижении предела текучести структура разрушается не сразу, а постепенно, по мере увеличения скорости сдвига.
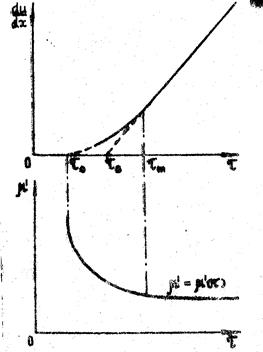 |
Рис.2. Линия консистентности и зависимость μ ’ от τ для реальной упруго-пластической системы.
Для характеристики механических свойств структуры в этом случае вводят три параметра: минимальный предел текучести (статическое напряжение сдвига), соответствующий началу течения жидкости τ 0; предел текучести по Бингаму (динамическое напряжение сдвига по Бингаму) τ Б; максимальный предел текучести (напряжение сдвига предельного разрушения структуры), при котором кривая переходит в прямую линию τ m (рис.2). Значение τ m равно напряжению, при котором структура в жидкости полностью разрушается.
Математическая модель упруго-пластической жидкости выражается следующей степенной зависимостью:
| τ – τ 0 = κ ﴾ | du | ﴿ n (3) |
| dx |
где κ – мера консистентности жидкости. С увеличением вязкости жидкости мера консистентности растет; n – степень неньютоновского поведения системы. Значение n всегда меньше единицы. Чем больше n отличается от единицы, тем сильнее проявляются неньютоновские свойства жидкости.
Кажущаяся вязкость системы определяется из соотношения
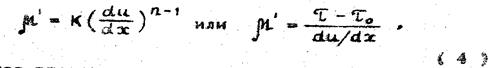
В качестве примера упруго-пластической жидкости можно указать на масляную краску, буровые растворы, высоко парафинистую дегазированную нефть с температурой ниже температуры насыщения парафином. Например, линии консистентности такой формы (рис.2) обнаружены у некоторых нефтей месторождений Азербайджана, Узбекистана, Казахстана.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
На практике наличие статического напряжения сдвига у жидкости часто играет положительную роль. Так, толщина слоя краски, оставленная после нанесения на вертикальную поверхность, определяется величиной τ 0. Следовательно, изменяя значение τ 0, можно регулировать резкой краски на покраску поверхности.
При бурении скважин процесс проходки часто прерывается. Применение качественных буровых растворов позволяет удерживать во взвешенном состоянии часть выше выбуренной породы и тем самым предотвращать поломку бурового инструмента. При этом регулирование параметров и размеров частиц удерживаемого в буровом растворе шлама достигается подбором параметра τ 0.
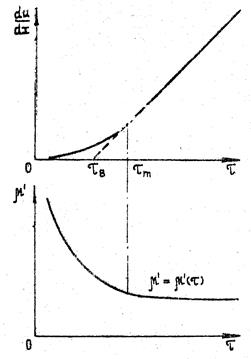
Рис.3. Линия консистентности и зависимость μ ’ от τ для вязкопластической системы.
То же самое наблюдается и при течении растворов высокомолекулярных соединений с гибкими, свернутыми в клубок макромолекулами, например, у водных растворов полимеров. Здесь снижение вязкости обусловлено распрямлением молекул и ориентацией в направлении потока. Система ведет себя при течении как жидкость, в которой взвешены частицы, способные ориентироваться или деформироваться.
Во всех этих случаях речь идет о кажущейся или эффективной вязкости, так как истинная вязкость жидкости от скорости течения не зависит.
Механические свойства псевдопластической жидкости характеризуются двумя параметрами: динамическим напряжением сдвига предельного разрушения структуры или ориентирования частиц в потоке τ m (рис.3). Реологическое уравнение у таких систем выражают в виде степенной зависимости
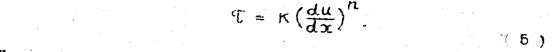
Кажущаяся вязкость вязко-пластической жидкости выражается следующим образом:
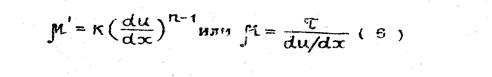
Здесь и в предыдущем случае необходимо иметь в виду, что для реальной жидкости n является переменным и зависящим от скорости сдвига. Поэтому при решении практических задач значение n следует определять в ограниченном пределе скоростей сдвига. Кроме того, неудобство использования степенного закона обусловлено зависимостью размерности меры консистентности от показателя степени.
В настоящее время для увеличения нефтеотдачи пластов, при воздействии на призабойную зону скважин и проведении изоляционных работ применяются растворы полимеров. В некоторых условиях в пористой среде они проявляют свойства дилатантных жидкостей.
Термин «дилатантная» можно применять для тех жидкостей, кажущаяся вязкость которых с увеличением скорости сдвига повышается (рис.4).
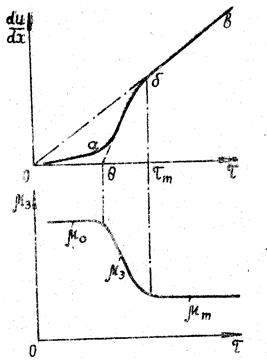
Рис.4. Линия консистентности и зависимость кажущейся вязкости от напряжения сдвига для дилатантной жидкости.
Такой тип течения был впервые обнаружен Рейнольдсом в суспензиях при большом содержании твердой фазы и крахмальных клейстерах. Рейнольдс при объяснении дилатантных свойств суспензий высказывает предположение о том, что в состоянии покоя твердые частицы имеют наиболее плотную упаковку, а пространство между частицами заполнено жидкостью. При течении суспензии с небольшой скоростью жидкость служит смазкой, уменьшающей трение между частицами, и напряжения сдвига невелики. При больших скоростях сдвига плотная упаковка частиц нарушается, увеличивается объем суспензии и уже при новой структуре жидкости ее недостаточно для смазки трущихся друг о друга частиц. Действующие напряжения сдвига при этом увеличиваются значительно быстрее, чем скорости сдвига.
Для описания реологического поведения дилатантной жидкости также применяют степенной закон, но с показателем степени больше единицы.
|
|
