Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Решение методом Монте-Карло

Для решения методом Монте-Карло будем моделировать экспоненциально-распределённую случайную величину.

В рассматриваемой системе имеется несколько простейших потоков: с одной стороны, идёт поток заявок на подключение к сети от пяти компьютеров, причём у каждого своя интенсивность 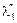, , 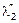, , 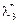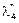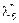. С другой стороны, каналы освобождаются компьютерами с интенсивностями 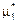, , 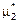, , 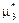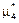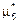. Время между наступлениями двух соседних событий для любого из этих восьми потоков моделируем следующим образом: генерируем случайное число 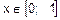, тогда время между наступлениями соседних событий в потоке с интенсивностью l определяем как .

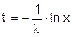1. Выбираем интервал наблюдения T, например T=20 суток (единицы измерения интервала должны совпадать с единицами измерения интенсивностей).

2. Для наблюдения за системой введём таблицу, в которой будем фиксировать состояние каждого компьютера (0 – не работает в сети, 1 – работает в сети и, соответственно, занимает канал) и время изменения текущего состояния. Предполагаем, что в начальный момент времени в сети компьютеров нет:

Для оценки вероятности отказа вводим два счётчика: счётчик попыток подключения (обращений) и счётчик отказов.

3. Моделируем работу системы по следующему алгоритму:

а) Находим минимальное время (это будет текущее время при наблюдении за системой), пусть номер этой строки i.

б) Если текущее состояние 0, значит, в это время произойдёт попытка подключения к сети, и надо увеличить счётчик обращений. Теперь проверяем, есть ли возможность подключиться, то есть смотрим, сколько компьютеров в данный момент в сети работают – считаем единицы в колонке состояний:

- Если их меньше количества каналов, компьютер к сети подключается (в столбце состояний ставим 1). Затем определяем, через какое время компьютер отключится: генерируем случайное число 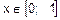, вычисляем величину 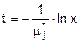и прибавляем её к текущему времени.

- Если все каналы заняты, состояние оставляем 0, увеличиваем счётчик отказов и определяем время следующей попытки подключения: генерируем случайное число 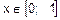, вычисляем величину 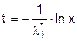и прибавляем её к текущему времени.

в) Если текущее состояние 1, значит, в это время компьютер отключается от сети. В столбце состояний ставим 0 и определяем время следующего подключения: генерируем случайное число 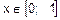, вычисляем величину 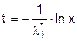и прибавляем её к текущему времени.

4. Наблюдение за системой продолжается до тех пор, пока минимальное время не превысит время наблюдения T.

5. Таких наблюдений за системой провести несколько и построить доверительный интервал для вероятности отказа.