Влияние выбора вычислительного алгоритма на результаты вычислений

Пример 3.2.1. Пусть необходимо вычислить значение выражения

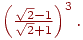
Избавившись от знаменателя, получаем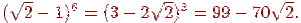

Полагая

а)

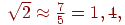
в)

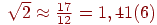
и рассматривая эти приближения как разные методы вычисления, получим следующие результаты:

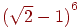
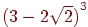
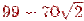
7/5	0, 004096	0, 008000
17/12	0, 005233	0, 004630	- 0, 1(6)

Очевидно, что столь значительное различие в результатах вызвано влиянием ошибки округления в задании .

Пример 3.2.2. Вычисление функции sin x с помощью ряда Тейлора.

Из курса математического анализа известно, что функция синус представляется своим рядом Тейлора

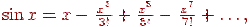
причем радиус сходимости ряда равен бесконечности — ряд сходится при любых значениях x.

Вычислим значения синуса при двух значениях аргумента. Пусть сначала 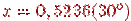. Будем учитывать лишь члены ряда, большие, чем 10^{- 4}. Выполнив вычисления с четырьмя значащими цифрами, получим sin (0.5236) = 0.5000, что соответствует принятой точности.

Пусть теперь 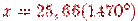. Если вычисления по данной формуле проводить с восемью значащими цифрами, то получим абсурдный результат: sin (25, 66) ≈ 24 (учитывались члены ряда, большие, чем 10^-8).

Разумеется, выходом из создавшейся ситуации может быть использование формул приведения.

Пример 3.2.3. Вычисление функции e^x с помощью ряда Тейлора.

Из курса математического анализа известно, что экспонента представляется своим рядом Тейлора

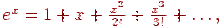
радиус сходимости этого ряда также равен бесконечности.

Приведем некоторые результаты расчетов (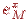 — значения экспоненты, вычисленные на компьютере).

x	ex	exM
	2, 718282	2, 718282
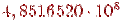
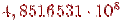
-1	0, 3678795	0, 3678794
-10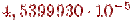
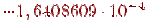
-20		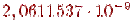1, 202966

Выходом из этой ситуации может быть использование для отрицательных аргументов экспоненты формулы

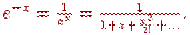
Естественно ожидать рост ошибок округления при вычислении рассматриваемой функции при больших значениях аргумента x. В этом случае можно использовать формулу e^x = e^{n + a} = eⁿe^a, где n = [x].

Пример 3.2.4. Рассмотрим следующий метод вычисления интеграла

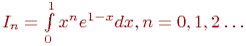
Интегрирование по частям дает

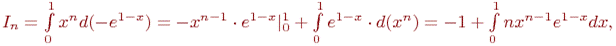
откуда следует

.

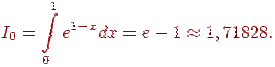
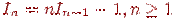Тогда

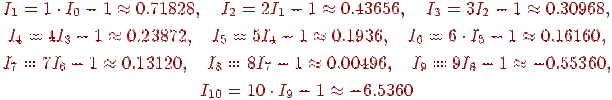
Очевидно, что отрицательные значения при n = 9, 10 не имеют смысла. Дело в том, что ошибка, сделанная при округлении I₀ до 6-ти значащих цифр сохранилась при вычислении I₁, умножилась на 2! при вычислении I₂, на 3! — при вычислении I₃, и так далее, т.е. ошибка растет очень быстро, пропорционально n!.

Пример 3.2.5. Рассмотрим методический пример вычислений на модельном компьютере, обеспечивающем точность 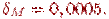Проанализируем причину происхождения ошибки, например, при вычитании двух чисел, взятых с точностью до третьей цифры после десятичной точки u = 1, 001, v = 1, 002, разность которых составляет Δ = |v_M - u_M| = 0, 001.

В памяти машины эти же числа представляются в виде

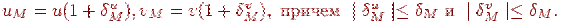
Тогда

Относительная ошибка при вычислении разности u_M - v_M будет равна

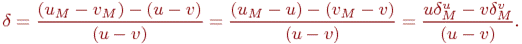
Очевидно, что 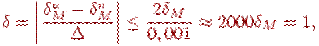т.е. все значащие цифры могут оказаться неверными.

Пример 3.2.6 Рассмотрим рекуррентное соотношение u_i+1 = qu_i, 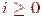, u₀ = a, q > 0, u_i > 0.

Пусть при выполнении реальных вычислений с конечной длиной мантиссы на i-м шаге возникла погрешность округления, и вычисления проводятся с возмущенным значением 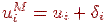, тогда вместо u_i+1 получим 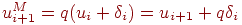, т.е.

Следовательно, если |q| > 1, то в процессе вычислений погрешность, связанная с возникшей ошибкой округления, будет возрастать (алгоритм неустойчив). В случае погрешность не возрастает и численный алгоритм устойчив.