Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Фізичні основи використання термокаротажу

Інтенсивність і поширення теплових полів залежить від термічних властивостей, геометричних форм і розмірів досліджуваних середовищ.

Термічні властивості гірських порід характеризуються коефіцієнтом теплопровідності або питомим тепловим опором, тепловою анізотропією, питомою теплоємністю і коефіцієнтом температуропровідності.

Коефіцієнт теплопровідності l визначається з відомого рівняння Фур’є:

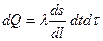, (5.1)

яке описує передачу тепла dQ за час dt через елемент середовища з поперечним перерізом ds, довжиною dl при перепаді температур dt. У рівнянні (5.1) l характеризує властивість середовища передавати теплову енергію її молекул і називається питомою теплопровідністю середовища. У системі СІ має розмірність Вт/м·градус.

Питомий тепловий опір x – величина, яка обернена питомій теплопровідності l, і має розмірність м·градус/Вт. Для різних гірських порід і корисних копалин x змінюється в широких межах – від тисячних до десятків м·градус/Вт. Він знижується зі збільшенням щільності, вологості, проникності і вмісту льоду в породі, підвищується при заміщенні в поровому просторі води нафтою, газом або повітрям і залежить від шаруватості порід (теплова анізотропія).

Теплова анізотропія порід характеризується безрозмірним коефіцієнтом

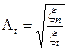, (5.2)

де x _n і x _t – питомі теплові опори породи по нормалі та по дотичній до напластування.

Так як в шаруватих породах x _n> x _t, то l _t> 1 (1, 015-1, 32).

Питома теплоємність С _р визначається з рівняння

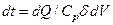, (5.3)

яке описує зміну температури dt тіла, що має об’єм dV і густину d, при наданні тілу тепла dQ. Коефіцієнт С _р у рівнянні (5.3) характеризує властивість середовища змінювати свою температуру. В системі одиниць СІ С _р має розмірність Дж/кг·градус. Для більшої частини гірських порід і корисних копалин С _р змінюється у відносно невеликих межах – від 580 до 2090 Дж/кг·градус, зростаючи зі збільшенням вологості.

Коефіцієнт температуропровідності а входить множником у диференціальне рівняння теплопровідності і має розмірність м²/с. Величина а визначається співвідношенням а=l/С_рd. Це комплексний параметр, що характеризує тепло-інерційні властивості гірських порід. Він виражає зміну температури одиниці об’єму середовища за одиницю часу. Гірські породи розрізняються за температуропровідністю більш ніж у 100 разів.

У розподілі природного теплового поля істотне значення має тепловий опір, а при вивченні нестаціонарних теплових процесів, при аналізі штучних теплових полів у свердловинах – теплоємність і температуропровідність гірських порід. Диференціація гірських порід і корисних копалин за термічними властивостями лежить в основі застосування термічних методів для вивчення геологічних розрізів свердловин, а теплова анізотропія гірських порід забезпечує можливість рішення тектонічних задач.

Аналіз теплових полів зводиться до рішення диференціального рівняння теплопровідності, що у випадку однорідного ізотропного середовища в системі прямокутних координат має вигляд:

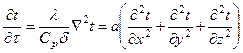, (5.4)

де ¶ t/ ¶ t – зміна температури t з часом t в точці з координатами x, y, z; Ñ ² t – лапласіан від функції t, що має в прямокутній системі координат наступне вираження:

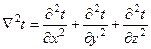. (5.5)

Інтегрування рівняння в умовах нестаціонарних теплових процесів, коли ¶ t/ ¶ t =0, є складною задачею, яку можна розв’язати лише для найбільш простих окремих випадків поширення тепла.

При сталому процесі теплообміну, коли ¶ t/ ¶ t =0, рівняння (5.4) перетвориться в рівняння Лапласа

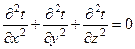. (5.6)