Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Прогнозування часових рядів за допомогою характеристик динаміки

У деяких найпростіших випадках для неперервного рівномірного ряду без коливань точковий прогноз можна зробити без аналітичного вирівнювання останнього за допомогою попередньо обчислених певних характеристик динаміки ряду:

1. Якщо всі абсолютні ланцюгові прирости 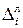рівні між собою (хоча б наближено), тобто рівні у_і часового ряду рівномірно зростають (коли 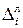> 0) або спадають (коли 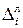< 0), то кожний наступний рівень, починаючи з
(п +1)-го, можна знаходити, додаючи до попереднього середній абсолютний приріст : у_{п +1}= у_п + . Очевидно, що в цьому випадку рівні ряду утворюють (хоча б наближено) арифметичну прогресію з різницею , що можна використовувати для виконання довгострокових прогнозів:

у_{п + l} = у_п + l · (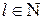). (4.29)

2. Якщо всі ланцюгові коефіцієнти зростання 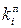рівні між собою (хоча б наближено), то кожний наступний рівень часового ряду, починаючи з
(п +1)-го, можна знаходити множенням попереднього на середній коефіцієнт зростання 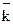: у_{п +1}= у_п · 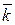. Очевидно, що в цьому випадку рівні ряду утворюють (хоча б наближено) геометричну прогресію із знаменником 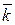, що можна використовувати для виконання довгострокових прогнозів:

у_{п + l} = у_п· (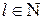). (4.30)

Слід підкреслити, що точкове прогнозування вищенаведеними наближеними способами слід вважати досить неточним, оскільки залежить від значення останнього рівня у_п часового ряду, яке може мати суттєво випадковий характер.