
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет газового цикла
|
|
25 вариантов задания приведены в табл. 1 приложения. Условия индивидуального задания берутся в соответствии с вариантом (графа 1).
Газовый цикл задан следующим образом: каждый из 4 процессов описан соответствующим показателем политропы (графы 2, 3, табл. 1 приложения); приведены термодинамические параметры некоторых точек цикла (графы 3–7, табл. 1 приложения); цикл отнесен к 1 кг воздуха.
Требуется произвести расчет газового цикла по законам и аналитическим зависимостям идеального газа.
1. Для каждого процесса, входящего в цикл, используя данные задания и характеристические уравнения, определить начальные и конечные параметры: давление, удельный объем, температуру, энтальпию, энтропию. Полученные результаты внести в табл. 8.1.1.
Таблица 8.1.1
| Точки | p | v | T | u | h | s | |||||
| Па | кгс/см2 | м3/кг | К | º С | кДж/кг | ккал/кг | кДж/кг | ккал/кг | кДж/кг· К | ккал/кг· º С | |
2. Определить характеристики цикла, используя аналитические зависимости соответствующих процессов и данные табл. 8.1.1. Полученные результаты внести в табл. 8.1.2 с учетом знака.
Таблица 8.1.2
| Процесс | ∆ u | ∆ h | ∆ s | q | l | |||||
| кДж/кг | ккал/кг | кДж/кг | ккал/кг | кДж/кг· К | ккал/кг· º С | кДж/кг | ккал/кг | кДж/кг | ккал/кг | |
| 1–2 | ||||||||||
| 2–3 | ||||||||||
| 3–4 | ||||||||||
| 4–1 |
3. Для цикла в целом определить подведенное тепло, отведенное тепло, работу цикла.
4. Перенести цикл по результатам расчета в T, s-и p, v-координаты.
5. Определить термический к.п.д. цикла. Сравнить полученный к.п.д. с термическим к.п.д. цикла Карно, совершенного при тех же крайних температурах.
Пример расчета
Вариант 0.
Цикл задан следующим образом:
p1 = 2 бар = 2 · 105 Па;
p2 = 12 бар = 12 · 105 Па;
v1 = 0, 45 м3/кг;
t3 = 300 º С;
n1–2 = k,
n2–3 = ∞,
n3–4 = k,
n4–1 = 0.
Решение.
1. Определим начальные и конечные параметры каждого процесса, входящего в цикл:
1–2 – адиабатный процесс, так как показатель политропы n = k. Для воздуха как двухатомного газа k =1, 4.
Запишем зависимость между параметрами газа в процессе: 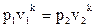 , где
, где
p1 = 2 бар = 2 · 105 Па, p2 = 12 бар = 12 · 105 Па, v1 = 0, 45 м3/кг, k =1, 4.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Тогда 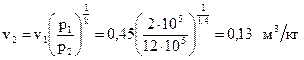 .
.
Запишем уравнение состояния идеального газа для точки 1: 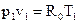 ,
,
где R0 – газовая постоянная, R0 = 287Дж/кг· К, тогда 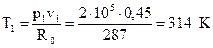 .
.
Запишем зависимость меду параметрами р и Т: 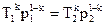 , тогда
, тогда 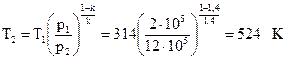
Для определения термодинамических функций находим изобарную и изохорную теплоемкости, используя закон Майера и выражение для показателя адиабаты: 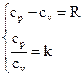 ;
; 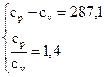 ;
; 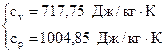 .
.
Вычислим внутреннюю энергию в точке 1: u1=cvT1=717, 75· 314=227 кДж/кг.
Вычислим энтальпию в точке 1: h1=u1+p1v1=227· 103 + 2· 105· 0, 45=317 кДж/кг.
Вычислим энтропию в точке 1:  .
.
2–3 – изохорный процесс, т.к. показатель политропы n = ∞.
Запишем зависимость между параметрами р и Т: 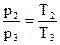 , где
, где
p1 = 2 бар = 2 · 105 Па, Т2=524 К, Т3=573 К, тогда 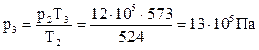 .
.
v3 = v2 = 0, 13 м3/кг, т.к. процесс изохорный (v = const).
Вычислим внутреннюю энергию в точке 2: u2=cvT2=717, 75· 524=379 кДж/кг.
Вычислим энтальпию в точке 2: h2=u2+p2v2=379· 103 +12· 105· 0, 13=535 кДж/кг.
Вычислим энтропию в точке 2: 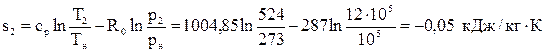 .
.
3–4 – адиабатный процесс, так как показатель политропы n = k. Для воздуха как двухатомного газа k =1, 4.
Запишем зависимость между параметрами газа в процессе: 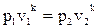 , где р3=13· 105 Па, v2 = 0, 13 м3/кг, р4 = 2· 105 Па (так как процесс 4–1 – изобарный, то р4=р1=2· 105 Па), k = 1, 4, тогда:
, где р3=13· 105 Па, v2 = 0, 13 м3/кг, р4 = 2· 105 Па (так как процесс 4–1 – изобарный, то р4=р1=2· 105 Па), k = 1, 4, тогда: 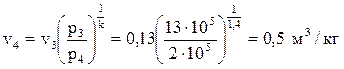 .
.
Вычислим внутреннюю энергию в точке 3: u3=cvT3=717, 75· 573=411 кДж/кг.
Вычислим энтальпию в точке 3: h3=u3+p3v3=411· 103 +13· 105· 0, 13=580 кДж/кг.
Вычислим энтропию в точке 3: 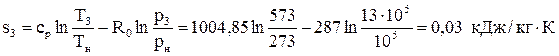 .
.
4–1 – изобарный процесс, так как показатель политропы n = 0.
Запишем уравнение состояния идеального газа для точки 4: 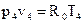 ,
,
где R0 – газовая постоянная, R0 = 287Дж/кг· К, тогда 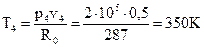 .
.
Вычислим внутреннюю энергию в точке 3: u4=cvT4=717, 75· 350=253 кДж/кг.
Вычислим энтальпию в точке 3: h4=u4+p4v4=253· 103 + 2· 105· 0, 5=353 кДж/кг.
Вычислим энтропию в точке 3: 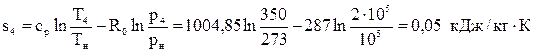 .
.
Таблица 8.1.1
| Точки | p | v | T | u | h | s | |||||
| Па | кгс/см2 | м3/кг | К | º С | кДж/кг | ккал/кг | кДж/кг | ккал/кг | кДж/кг· К | ккал/кг· º С | |
| 2· 105 | 2, 04 | 0, 45 | 54, 05 | 74, 48 | –0, 05 | –0, 0119 | |||||
| 12· 105 | 12, 24 | 0, 13 | 90, 24 | 127, 38 | –0, 05 | –0, 0119 | |||||
| 13· 105 | 13, 26 | 0, 13 | 97, 86 | 138, 1 | 0, 03 | 0, 0071 | |||||
| 2· 105 | 2, 04 | 0, 5 | 60, 24 | 84, 05 | 0, 05 | 0, 0119 |
2. Определим характеристики цикла, используя аналитические зависимости соответствующих процессов.
1–2 – адиабатное сжатие.
Вычислим изменение внутренней энергии: 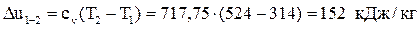 .
.
Вычислим изменение энтальпии: 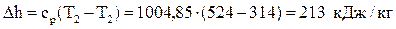 .
.
Вычислим изменение энтропии: ∆ s = 0; s = const.
Вычислим теплоту: q1–2 = 0.
Вычислим работу: l = –∆ u = –152 кДж/кг.
2–3 – изохорное нагревание.
Вычислим изменение внутренней энергии: 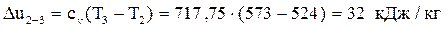 .
.
Вычислим изменение энтальпии: 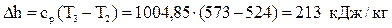 .
.
Вычислим изменение энтропии: 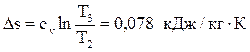 .
.
Вычислим теплоту: q1–2 = ∆ u = 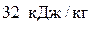 .
.
Вычислим работу: l = 0.
3–4 – адиабатное расширение.
Вычислим изменение внутренней энергии: 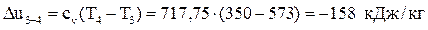 .
.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Вычислим изменение энтальпии: 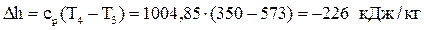 .
.
Вычислим изменение энтропии: ∆ s = 0; s = const.
Вычислим теплоту: q3–4 = 0.
Вычислим работу: l = –∆ u = –158 кДж/кг.
4–1 – изобарное сжатие.
Вычислим изменение внутренней энергии: 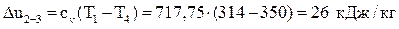 .
.
Вычислим изменение энтальпии: 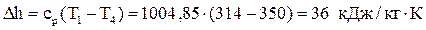 .
.
Вычислим изменение энтропии: 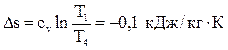 .
.
Вычислим теплоту: q4–1 = сp(T1 – T4)= 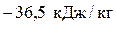 .
.
Вычислим работу: 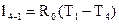 =287, 1· (314 – 350) = –10
=287, 1· (314 – 350) = –10 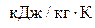 .
.
| Процесс | ∆ u | ∆ h | ∆ s | q | l | |||||
| кДж/кг | ккал/кг | кДж/кг | ккал/кг | кДж/кг· К | ккал/кг· º С | кДж/кг | ккал/кг | кДж/кг | ккал/кг | |
| 1–2 | 36, 19 | 50, 71 | –152 | –36, 19 | ||||||
| 2–3 | – 32 | –7, 62 | 10, 71 | 0, 08 | 0, 019 | 7, 62 | ||||
| 3–4 | –158 | –37, 62 | –226 | –53, 81 | 37, 62 | |||||
| 4–1 | 6, 19 | 8, 57 | –0, 1 | –0, 024 | –36, 5 | –8, 69 | –10 | –2, 38 |
Таблица 8.1.2
3. Для цикла в целом определяем:
подведенное тепло 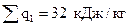 ;
;
отведенное тепло 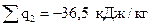 ;
;
работу цикла 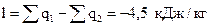 .
.
4. Переносим цикл по результатам расчета в T, s- и p, v-координаты.
5. Определяем термический к.п.д. цикла. Сравниваем полученный к.п.д. с термическим к.п.д. цикла Карно, совершенного при тех же крайних температурах.
Термический к.п.д. данного цикла 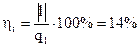 .
.
Термический к.п.д. цикла Карно 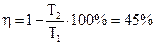 .
.
Термический к.п.д. цикла Карно, совершаемого при тех же крайних температурах, что и данный цикл, на 31% выше. Для получения более высокого к.п.д. цикла необходимо увеличивать разность между крайними температурами.
|
|
