
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формирование уравнений цепи с зависимыми источниками энергии и их решение
|
|
Выбор метода расчёта цепи определяется типом зависимых источников. Перед расчётом целесообразно независимые и зависимые источники преобразовать в один тип. Если для расчёта цепи выбран метод контурных токов, то все источники энергии целесообразно преобразовать в ИНУТ, выразив управляющие напряжения Uky или токи Iky через искомые контурные токи, а перед записью уравнений МУН – целесообразно все источники преобразовать в ИТУН, выразив управляющие напряжения Uky или токи Iky через узловые напряжения.
В качестве примера проведём расчёт цепи (рис. 13.2, а) с зависимым источником типа ИТУH 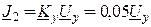 , управляемый напряжением
, управляемый напряжением 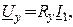 методом узловых напряжений. Управляющим параметром здесь является передаточная проводимость
методом узловых напряжений. Управляющим параметром здесь является передаточная проводимость 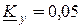 См.
См.
1. Преобразуем независимый источник напряжения Е 1 c параметрами 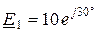 В и
В и 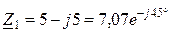 Ом в эквивалентный источник тока с параметрами Y 1 = 1/ Z 1 =
Ом в эквивалентный источник тока с параметрами Y 1 = 1/ Z 1 =  Cм и J 1 = Е 1 Y 1 =
Cм и J 1 = Е 1 Y 1 = 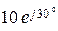 ´ ´
´ ´ 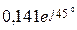 =
= 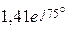 А (рис. 13.2, б).
А (рис. 13.2, б).
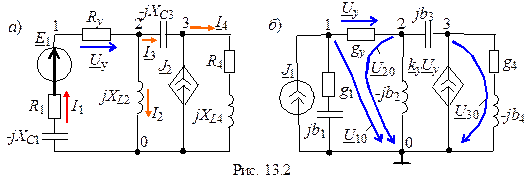
2. Выбрав базисный узел 0 и направление комплексов узловых напряжений U 10, U 20 и U 30 (рис. 13.2, б), составим систему узловых уравнений:
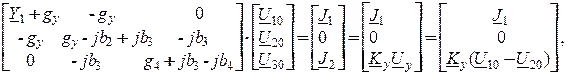
 |
где комплексное межузловое напряжение
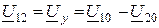 .
.
3. Сгруппировав одноимённые элементы матриц, т. е. проведя поэлементное сложение матрицы комплексных проводимостей, получим:
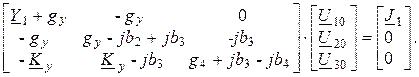
4. Пусть известны комплексы проводимостей элементов цепи:
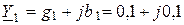 См; gу = 0, 05 См; - jb 2 = - j 0, 05См; j
См; gу = 0, 05 См; - jb 2 = - j 0, 05См; j  См; g 4 = 0, 1 См;
См; g 4 = 0, 1 См; 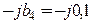 См.
См.
Подставив численные значения параметров элементов цепи в матричное уравнение (см. п. 3), имеем:
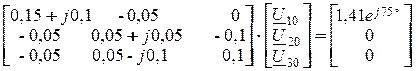

5. Воспользовавшись программой ElСalce (рис. 13.3), получаем комплексы узловых напряжений:
U 10 » 8, 687 еj 38, 7 °В; U 20 » 3, 407 еj 50° В и U 30 » 3, 614 еj 95°В.
6. Токи ветвей определим по обобщённому закону Ома (см. рис. 13, 2, а):
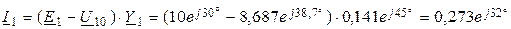 А;
А;
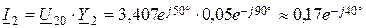 А;
А;
 А;
А;
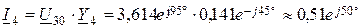 А.
А.
7. Управляющее напряжение зависимого источника
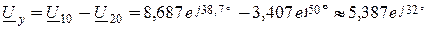 В,
В,
а ток источника тока 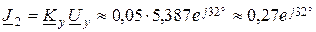 А.
А.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
 |
8. Проверка результатов расчёта:
- уравнение второго закона Кирхгофа для левого контура цепи (см. рис. 13.2, а):
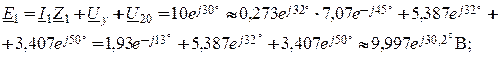
- уравнение первого закона Кирхгофа для узла 3:
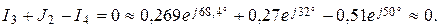
|
|
