Представление моделей электромеханических систем в пространстве состояний. Общая постановка задачи Коши

Пусть электромеханическая система (ЭМС) имеет переменные состояния 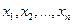. Переменные состояния – это те величины, которые определяют энергетическое состояние ЭМС. В качестве таких величин могут выступать токи через катушки индуктивности, напряжения на конденсаторах, скорости вращения двигателей и т. д. Математическую модель ЭМС можно представить в виде системы дифференциальных уравнений (СДУ) 1-го порядка, записанной в нормальной форме Коши, то есть разрешенной относительно производных:

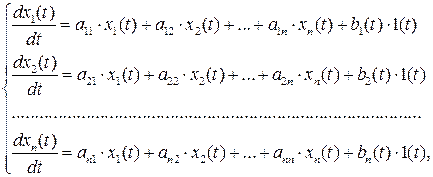
(1)

где 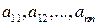– постоянные коэффициенты, образующие матрицу коэффициентов:

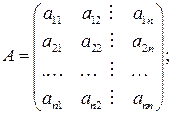
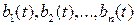– независимые свободные члены дифференциальных уравнений (ДУ), образующие вектор-функцию членов ДУ:

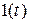– функция Хэвисайда или единичное ступенчатое воздействие.

ДУ 1-го порядка, связывающее некоторую функцию 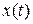и ее производную

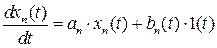
является неоднородным, так как включает в себя свободный член 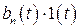. При равенстве 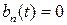данное ДУ становится однородным.

То же самое можно сказать о СДУ (1). Если данная система содержит вектор свободных членов 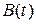, то СДУ является неоднородной. При условии 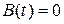СДУ становится однородной.

Модель ЭМС можно записать в векторно-матричной форме

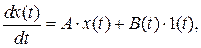
где 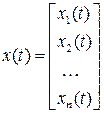– вектор переменных состояния ЭМС.

Вышеприведенную модель ЭМС можно представить несколько подробнее:

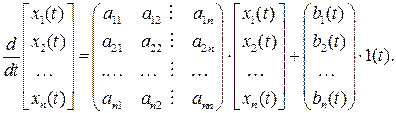
Одним из электромеханических преобразователей энергии в регулируемом электрическом приводе является двигатель постоянного тока независимого возбуждения (ДПТ НВ).

Схема подключения ДПТ НВ к источнику постоянного напряжения U представлена на рис. 1.

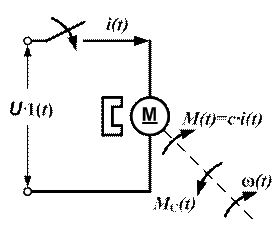
Рис. 1. Схема подключения ДПТ НВ к источнику постоянного напряжения

Схема замещения якорной цепи ДПТ НВ показана на рис. 2.

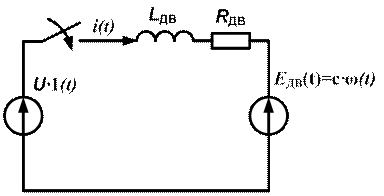
Рис. 2. Схема замещения якорной цепи ДПТ НВ

При составлении математической модели ДПТ НВ примем следующие допущения. Считаем, что реакция якоря полностью скомпенсирована (в реальном ДПТ всегда есть компенсационная обмотка либо добавочные полюса), поток возбуждения постоянен, а активное сопротивление якорной цепи не изменяется во время работы двигателя.

Запишем дифференциальное уравнение электрического равновесия якорной цепи двигателя (рис. 12):

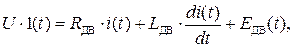
где 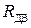– суммарное активное сопротивление последовательно включенных обмотки якоря и добавочных полюсов в горячем состоянии (при 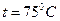); 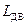– суммарная индуктивность якорной цепи; – противо-ЭДС двигателя; 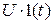– напряжение, приложенное к якорной цепи; 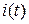– ток якорной цепи.

Уравнение механического равновесия двигателя:

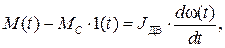
где 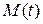– электромагнитный момент ДПТ НВ; – момент сопротивления нагрузки; 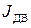– суммарный момент инерции, приведенный к валу двигателя; 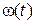– скорость двигателя.

Учитывая, что 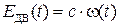и (c – коэффициент ЭДС и момента ДПТ НВ), запишем систему дифференциальных уравнений:

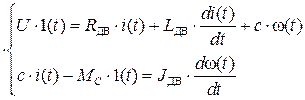
СДУ в нормальной форме Коши:

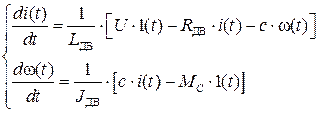
СДУ в матричном виде:

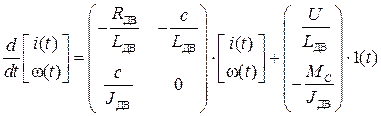
Здесь:

– матрица коэффициентов перед переменными состояния;

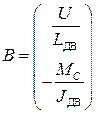– вектор свободных членов СДУ;

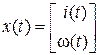– вектор переменных состояния.

Из полученной математической модели ДПТ НВ видно, что переменными состояния в нем являются скорость вала и ток в якорной цепи. Эти переменные состояния соответственно связаны с массой вала и индуктивностью обмотки якоря, то есть с механической и электрической инерционностями двигателя.

Рассмотрим различные методы решения системы дифференциальных уравнений, описывающих динамику ДПТ НВ.

Рис. 3. Методы решения ДУ

Численные методы – это алгоритмы вычисления приближенных значений неизвестной функции на некоторой выбранной сетке аргументов. С помощью численных методов возможно найти частное решение (в зависимости от начальных условий) как обыкновенных дифференциальных уравнений, так и уравнений в частных производных.

Численные методы делятся на одношаговые и многошаговые. В первом случае для получения решения в каждом новом расчетном узле достаточно иметь значение функции только в предыдущем узле. Для применения многошаговых численных методов требуется знание результата расчета неизвестной функции на нескольких предыдущих шагах, которые получают обычно одношаговыми методами (например, Эйлера или Рунге-Кутта). К многошаговым относятся методы прогноза и коррекции, Милна, Хемминга, Адамса-Башфорта, Нюстрема.