Магнетизм коллективизированных электронов.

2.1. Постоянное магнитное поле в веществе.

Магнетизм – особая форма взаимодействия, возникающая между движущимися электрически заряженными частицами. Вид материи, через которую передаётся силовое воздействие на движущиеся заряды и тела, обладающие магнитным моментом, называется магнитным полем. Необходимо отметить, что и электрическое, и магнитное поля – являются отдельными проявлениями более общего – электромагнитного поля. Однако между электрическим и магнитным полями нет полной симметрии. Так, источниками электрического поля являются электрические заряды, а их носителями – элементарные частицы (электроны, протоны, мезоны и т.д.). Аналогичных магнитных зарядов в природе выявлено не было. В 1931 г. П. Дирак обосновал возможность существования магнитных монополей – магнетонов, которые подобно фононам можно в общем случае отнести к квазичастицам. В соответствии с современными представлениями о природе магнетизма, единственными материальными носителями магнитного поля, являются подвижные электрические заряды. Магнитные свойства вещества объясняются тем, что в масштабах атома, электроны и нуклоны имеют два типа токов – орбитальные, связанные с перемещением в пространстве центров масс этих частиц и спиновые – связанные с внутренними степенями свободы их движения. На основании экспериментальных данных и теоретического обобщения основных представлений о природе магнетизма, можно сделать вывод о том, что единственными источниками магнитного поля в вакууме являются движущиеся свободные электрические заряды или токи в проводниках. В веществе магнитное поле создаётся также ещё и движущимися зарядами самих атомов и молекул. Это, в частности, подтверждает гипотезу Ампера о том, что магнетизм самого вещества можно объяснить наличием микроскопических электрических токов, равномерно распределённых по всему объёму вещества. Так, согласно полуклассической теории Резерфорда-Бора, электроны в атомах вращаются по замкнутым круговым орбитам вокруг позитивно заряженного ядра. Вместе с тем, электроны совершают вращательное движение вокруг собственных осей, и с этими внутренними движениями связан определённый механический момент импульса, который называется спином электрона. Спиновый момент имеет также и ядра атомов. Орбитальный и спиновый моменты движения заряженных частиц создают микротоки, которые и являются источниками магнитного поля в веществе. Современные представления существенно отличаются от теории Резерфорда-Бора, однако важным здесь является то, что эти частицы находятся в непрерывном движении и с этими движениями связаны механический и магнитный моменты. Так, согласно современным представлениям, магнитные свойства вещества обусловлены тремя основными причинами: орбитальным магнитным моментом электронов, который возникает вследствие их движения вокруг ядра; магнитным моментом электронов, находящихся в определённом соотношении с их собственным механическим моментом – спином; собственным магнитным моментом атомных ядер. Поскольку движение атомных ядер, вследствие их массы, гораздо меньше по сравнению с движением электронов, то соответственно магнитные моменты атомных ядер – на несколько порядков меньше орбитальных и спиновых моментов самих электронов. Поэтому при рассмотрении магнитных свойств вещества, магнитными моментами самих ядер пренебрегают. Для получения результирующего магнитного момента атома или молекулы, складывают магнитные моменты электронов и ядер на основании принципа суперпозиции полей. В зависимости от электронного строения атомов или молекул, орбитальные и спиновые моменты электронов могут взаимно компенсировать друг друга, и тогда их суммарный магнитный момент будет равен нулю (т.е. может отсутствовать магнитный момент). Если же электронная структура атома или молекулы такова, что такой скомпенсированности моментов (орбитального, спинового) нет, то суммарный магнитный момент такой частицы будет отличен от нуля. В отсутствии внешнего магнитного поля, вещества – атомы или молекулы которых не имеют магнитного момента – не создают дополнительного магнитного поля, их орбитальный и спиновый моменты скомпенсированы. В случае наличия у атомов и молекул вещества магнитного момента (их орбитальный и спиновый моменты не скомпенсированы), отсутствие дополнительного магнитного поля объясняется тем, что вследствие хаотического теплового движения атомов или молекул вещества, магнитные моменты последних в произвольный момент времени ориентируются в пространстве статистически равномерно и таким образом, возбуждаемые ими магнитные поля будут взаимно компенсироваться. При внесении произвольного вещества в магнитное поле, оно намагничивается. При этом в атомах или молекулах вещества, не имеющего магнитного момента, последний наводится. При внесении же вещества, атомы или молекулы которого имеют магнитный момент, происходит ориентация последнего в направлении поля, и как следствие, вещество будет становиться источником дополнительного магнитного поля. Таким образом, вещества во внешнем магнитном поле становятся источниками дополнительного магнитного поля. При этом в каждой точке пространства, где есть вещество, индукция магнитного поля будет равна векторной сумме индукций внешнего магнитного поля и магнитного поля самого магнетика. Приобретение веществом магнитных свойств, называется его намагничиванием. Все магнетики, в общем случае, можно разделить на три основных класса: диамагнетики, парамагнетики и ферромагнетики. В ряде случаев выделяют ещё один класс веществ, называемых ферримагнетиками. Большинство классов веществ во внешнем магнитном поле намагничиваются слабо, к таким веществам относят диа- и парамагнетики. Сильными магнитными свойствами обладают только ферромагнетики, к которым относят такие вещества как железо, никель, кобальт, сплавы этих веществ и т.д. Магнитные поля, возбуждаемые орбитальным и спиновым движениями электронов и атомных ядер, являются эквивалентными соответствующим полям токов, проходящих в атомах вещества. Эти токи называют молекулярными. Вследствие хаотического движения атомов, значения и направление молекулярных токов постоянно изменяется в пространстве и во времени. Для характеристики магнитных полей в магнетиках, вводят макроскопические параметры, являющиеся результатом усреднения соответствующих им микроскопических параметров по физически бесконечно малому объёму. Как и для случая вакуума, вводят вектор магнитной индукции 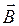. С учётом молекулярных токов проводимости, вводят соответствующие им вектора плотности тока намагниченности 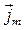и тока проводимости, обозначаемого 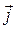. Тогда, уравнения справедливые для случая вакуума, окажутся справедливыми и для характеристики постоянного магнитного поля в веществе, то есть имеем в интегральной:

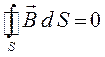
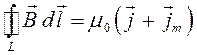
и соответственно в дифференциальной формах:

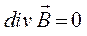
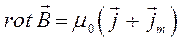
Для характеристики намагниченности однородного магнетика, вводят вектор намагниченности 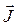, численно равный суммарному магнитному моменту 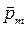единицы объёма намагниченного вещества:

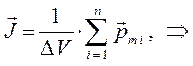
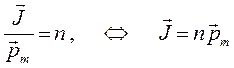
Для элемента объёма 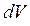, элементарный магнитный момент, очевидно, будет равен:

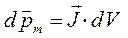
здесь 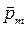– средний магнитный момент молекулярных токов одной молекулы и 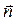– среднее число частиц (атомов, молекул, ионов).

Очевидно, что:

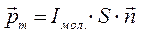
Вектор намагниченности 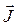имеет размерность вида:

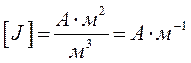
Как известно, в электростатике аналогом вектора намагниченности 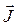является вектор поляризации 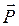. Для того чтобы установить связь между вектором намагниченности 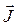и объёмной плотностью токов намагничивания 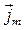, рассмотрим замкнутый контур 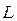, ограничивающий поверхность 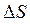намагниченного магнетика и посчитаем циркуляцию вектора намагниченности вдоль этого контура:

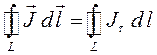
здесь 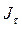– тангенциальная составляющая вектора намагниченности на контур 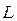. Так, на основании полученного нами выше общего выражения вида:

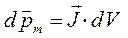
или после соответствующих подстановок и преобразований:

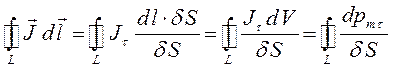
а также учитывая, что:

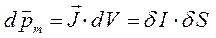
будем иметь соответственно:

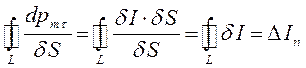
где 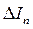– нормальная составляющая силы тока, пересекающая элементарную площадку 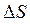. Выражение для циркуляции вектора намагниченности, будет:

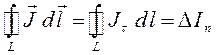
Воспользовавшись понятием ротора вектора, полученное выражение можно будет далее представить к виду:

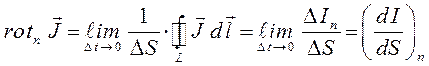
Учитывая, что:

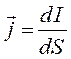
имеем соответственно:

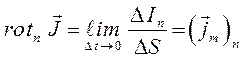
и от равенства нормальных составляющих векторов, переходим к равенству соответствующих векторов, т.е.

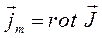
Полученное нами выше выражение устанавливает связь между векторами намагничивания и плотностью токов намагничивания. Таким образом, магнитное поле в магнетиках можно описать уравнениями для вакуума, однако при этом необходимо учитывать токи намагничивания. Полученные нами выше уравнения:

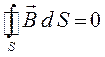
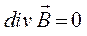
свидетельствуют о том, что не только в вакууме, но и в магнетиках – магнитных зарядов нет и таким образом, поток вектора магнитной индукции сквозь замкнутую поверхность будет равен нулю. Это в свою очередь означает, что, сколько силовых линий входит в объём 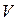, ограниченный замкнутой поверхностью , столько же и выходит, так как силовые линии магнитного поля токов – замкнутые. Другая пара уравнений вида, соответственно в формах:

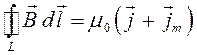
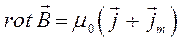
позволяет говорить о вихревом характере магнитного поля – как в вакууме, так и в магнетиках, в отличие от электростатического поля, которое является безвихревым. Данные уравнения о циркуляции векторного поля фактически подразумевают работу сил Ампера и являются выражением закона полного тока, с учётом токов намагничивания в магнетиках. Поскольку, как это было показано выше:

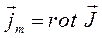
тогда равенство вида:

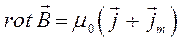
может быть переписано в виде:

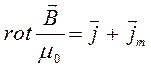
откуда соответственно:

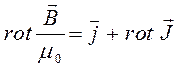
и таким образом имеем:

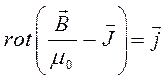
или принимая:

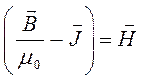
имеем:

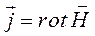
здесь 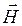– вектор напряжённости магнитного поля. Напряжённость магнитного поля не является чисто силовой характеристикой магнитного поля, т.к. включает в себя вектор намагничивания вещества 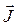. Однако поскольку в полученное выше дифференциальное выражение плотность токов намагничивания не входит, то в однородных изотропных магнетиках, где существует магнитное поле при неизменной конфигурации токов, нет необходимости знать закон распределения токов намагничивания, достаточно определить плотность тока проводимости 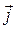. Отсюда следует, что напряжённость магнитного поля будет характеризовать лишь ту часть магнитного поля, которое возбуждается токами проводимости. Таким образом, напряжённость магнитного поля 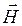в магнетиках играет ту же самую роль, что и вектор электрического смещения (индукции) 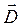электрического поля в диэлектрике, а вектор магнитной индукции 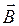– соответствует напряжённости электрического поля 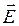. Таким образом, будем иметь соответственно:

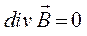
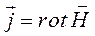
Полученные уравнения, есть дифференциальная форма записи для постоянного магнитного поля в магнетиках. Данные дифференциальные уравнения можно записать также в интегральной форме:

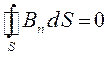
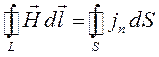
Зависимость 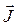от 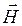в общем случае имеет сложный характер и в макроскопической электродинамике её устанавливают опытным путём. Как показали исследования, для многих изотропных магнетиках (диа- и парамагнетиков) зависимость векторов намагниченности от напряжённости магнитного поля, носит линейный характер, тогда соответственно:

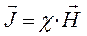
где 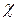– магнитная восприимчивость вещества. Для вакуума её значение равно нулю, для произвольного, любого вещества она отлична от нуля. Это, в свою очередь показывает, что все вещества способны намагничиваться, являясь, таким образом, магнетиками. Для линейных магнетиков, то есть таких, для которых имеет место линейная зависимость вектора намагничивания от напряжённости магнитного поля, коэффициент 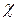мало отличен от единицы. При этом для диамагнетиков магнитная восприимчивость вещества 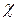меньше нуля (негативная), то есть направление вектора намагничивания 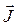– противоположен вектору 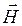, поэтому внешнее поле ослабляется, то есть магнитный поток выталкивается, что в свою очередь приводит к выталкиванию вещества из магнитного поля.Для парамагнетиков, величина 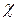больше нуля (положительная), направление вектора намагничивания вещества 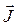– совпадает с направлением вектора напряжённости магнитного поля 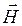и внешнее поле усиливается, то есть магнитный поток втягивается в образец, что в свою очередь приводит к втягиванию вещества в магнитное поле. Из линейного равенства вида:

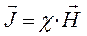
следует, что 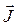имеет ту же размерность, что и 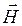. Из выражения для напряжённости магнитного поля:

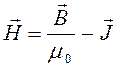
следует, что:

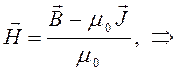
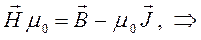
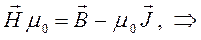
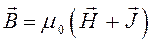
Таким образом, как это следует из полученных нами выше выражений, магнитное поле в магнетиках слагается из внешнего магнитного поля и магнитного поля намагниченного магнетика 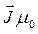. Учитывая линейную зависимость между векторами намагниченности 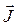и напряжённости магнитного поля 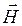, получим уравнение, связывающее напряжённость магнитного поля с индукцией этого поля:

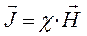
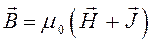
тогда:

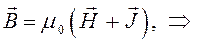
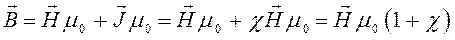
и таким образом:

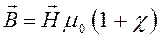
Принимая выражение:

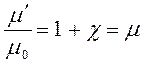
будем иметь соответственно:

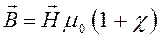
откуда будем иметь соответственно:

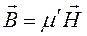
Поскольку:

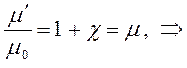
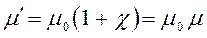
тогда:

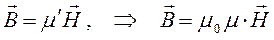
В полученном нами выше выражении:

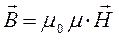
величина 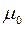представляет собой магнитную проницаемость вакуума; 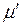– абсолютную магнитную проницаемость вакуума и 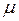– относительную магнитную проницаемость вакуума. Относительная магнитная проницаемость вещества 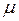является макроскопическим параметром и для каждого однородного, изотропного магнетика является величиной постоянной. Она может быть большей или меньшей единицы. Магнитную проницаемость в общем случае определяют экспериментально и далее вычисляют величины 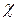, 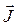и .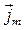

2.2. Классификация магнетиков.

Все магнетики, в общем случае, можно разделить на три основных класса: диамагнетики, парамагнетики и ферромагнетики. В ряде случаев выделяют ещё один класс веществ, называемых ферримагнетиками. Как было показано выше, все вещества в общем случае способны намагничиваться, являясь, таким образом, магнетиками. При этом для диамагнетиков магнитная восприимчивость вещества 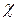меньше нуля (негативная), то есть направление вектора намагничивания 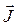– противоположен вектору 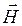, поэтому внешнее поле ослабляется, то есть магнитный поток выталкивается, что в свою очередь приводит к выталкиванию вещества из магнитного поля.Для парамагнетиков, величина 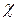больше нуля (положительная), направление вектора намагничивания вещества 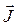– совпадает с направлением вектора напряжённости магнитного поля 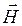и внешнее поле усиливается, то есть магнитный поток втягивается в образец, что в свою очередь приводит к втягиванию вещества в магнитное поле.

2.2.1. Диамагнетики.

К диамагнетикам относят вещества, в атомах которых орбитальные и спиновые моменты электронов, при условии отсутствия внешнего магнитного поля, являются взаимно скомпенсированными. Таким образом, атомы диамагнетиков не имеют собственного магнитного момента. Это имеет место в атомах, молекулах или ионах с полностью застроенными электронными оболочками. Суммарный спиновой момент таких систем равняется нулю, что соответствует синглетному состоянию. Магнитные моменты электронов в таких системах, взаимно компенсируются, поскольку в этих оболочках все квантовые состояния заняты и вдоль каждого направления устанавливается определённое количество спаренных электронов с противоположно направленными орбитальными и спиновыми моментами. При внесении диамагнетика во внешнее магнитное поле, в электронных оболочках атомов, молекул или ионов возникает индуцированные круговые токи. Эти токи создают дополнительный магнитный момент, направленный в таких системах против внешнего магнитного поля, ослабляя последнее. Свойство вещества намагничиваться против внешнего магнитного поля, называется диамагнетизмом. Диамагнитный эффект свойственен всем веществам, так как он связан с возникновение дополнительных круговых движений электронов в атомах или молекулах вещества и изменением частоты их вращения при внесении диамагнетиков во внешнее магнитное поле. Так, согласно полуклассической теории Резерфорда-Бора, электрон вращается вокруг ядра по круговым орбитам. Тогда магнитный момент электрона будет определяться выражением вида:

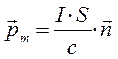
учитывая, что:

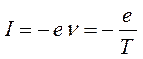
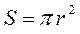
имеем соответственно:

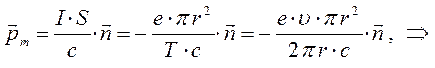
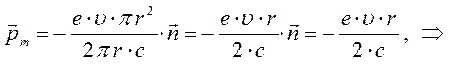
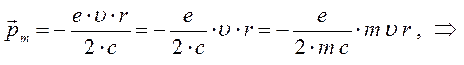
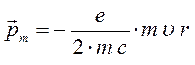
Учитывая, что:

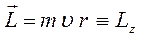
будем иметь соответственно:

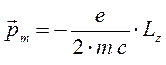
или

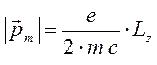
откуда следует, что:

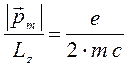
или

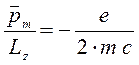
здесь выражение:

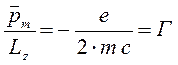
есть гиромагнитное или орбитальное магнитно-механическое соотношение. Так, учитывая, что по определению:

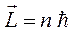
после соответствующей подстановки в исходное выражение для магнитного момента 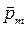, будем иметь соответственно:

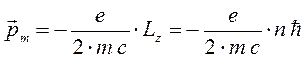
откуда соответственно:

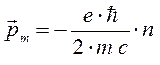
или

Очевидно, что при :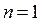

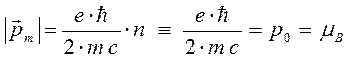
здесь 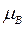– магнетон Бора. Данная величина является константой (постоянной) и принимает значение, равное:

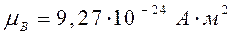
Электрон помимо орбитального, имеет ещё и спиновой момент (собственный угловой момент). Проекция спина на заданное направление, может принимать одно из двух возможных значений 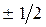. Спину отвечает магнитный момент, значение которого равно магнетону Бора, то есть со спином связано гиромагнитное соотношение, которое в два раза больше орбитального. Магнитные моменты произвольного атома являются векторной суммой орбитальных и спиновых магнитных моментов электронов, т.е. 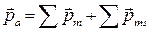. В 1895 г. Дж. Лармор предложил теорию, в основе которой лежали представления о так называемом прецессионном движении, согласно которой атом подобно гироскопу в магнитном поле совершает круговые (прецессионные) движения, вследствие чего атом приобретает дополнительный магнитный момент, направленный против внешнего магнитного поля, что в свою очередь и является причиной возникновения диамагнетизма. Такие круговые (прецессионные) движения атома получили название ларморовской прецессией. Вследствие этого диамагнитное вещество при внесении его в магнитное поле, будет намагничиваться против внешнего поля с магнитной индукцией .

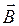2.2.2. Парамагнетики.

Вещества, частицы которых (атомы, молекулы, ионы) имеют собственный магнитный момент 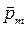, называются парамагнетиками, а их свойство намагничиваться во внешнем магнитном поле в направлении поля с индукцией 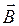, называется парамагнетизмом. К парамагнитным относят частицы вещества – атомы, молекулы и ионы, имеющие неспаренные электроны. Так, если нет внешнего магнитного поля, частицы парамагнитных веществ находятся в неупорядоченном хаотическом движении, за счёт которых магнитные моменты и создаваемые таким образом поля, ориентируются хаотично и равновероятно по всем направлениям; при этом магнитные моменты вследствие постоянной переориентации частиц взаимно погашаются. Во внешнем магнитном поле, на элементарные носители магнитных моментов 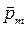действует ориентирующая сила, старающаяся изменить угол между векторам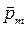и и 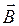. Поэтому при внесении парамагнетика во внешнее магнитное поле, магнитные моменты будут ориентироваться в направлении индукции силового поля, и парамагнетик будет намагничиваться. Поскольку направление индукции поля намагничивания магнетика будет совпадать с направлением индукции внешнего магнитного поля, то последнее будет усиливаться. С ростом индукции 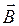внешнего поля, будет увеличиваться ориентирующее его действие на элементарные магнитные моменты, и намагниченность будет увеличиваться линейно, т.е.

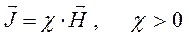
Результирующая индукция магнитного поля в парамагнетиках определяется на основании выражения 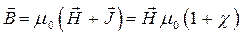. В достаточно сильном внешнем магнитном поле все магнитные моменты в парамагнитных частицах будут ориентироваться в направлении поля и, в конце концов, будет достигнуто магнитное насыщение, то есть когда:

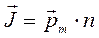
С повышением температуры будет увеличиваться неупорядоченное тепловое движение частиц, что приведёт в конечном итоге к нарушению в упорядочении ориентации магнитных моментов и как следствие – с повышением температуры будет наблюдаться уменьшение магнитной восприимчивости вещества Температурная зависимость магнитной восприимчивости парамагнетиков от температуры, выражается законом Кюри:

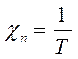
для парамагнитных газов применима также теория Лонжевена:

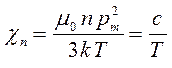
для жидкостей и твёрдых веществ, применим закон Кюри-Вейса, учитывающий взаимодействие между частицами вещества:

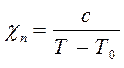
Особенностью парамагнетиков является то, что после прекращения действия внешнего магнитного поля, упорядоченная ориентация магнитных моментов вследствие теплового, хаотического движения частиц вновь разрушается.

2.2.3. Ферромагнетики.

Сильномагнитные свойства наблюдаются у веществ, находящихся в твёрдом состоянии. Такие вещества состоят преимущественно из атомов с незастроенными внутренними оболочками. Атомы ферромагнетиков имеют нескомпенсированные собственные магнитные моменты, которые благодаря внутренним взаимодействиям могут приобретать определённую упорядоченность в пространственной ориентации, вследствие чего вещество намагничивается. Вещества, которые при определённых условиях могут самостоятельно (спонтанно) намагничиваться, а магнитная их восприимчивость зависит от напряжённости внешнего магнитного поля, а также от последовательности прохождения различных магнитных состояний, называют ферромагнетиками. Особенностью ферромагнетиков является то, что они могут иметь макроскопическую намагниченность без внешнего магнитного влияния. Магнитная восприимчивость ферромагнетиков много больше нуля 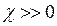и может достигать значений 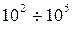, то есть внешнее магнитное поле в средине ферромагнетиков усиливается в 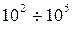раз. Как говорилось уже ранее, намагничивание диамагнетиков состоит в возникновении микроскопических индукционных токов и соответственно дополнительных магнитных моментов частиц вещества, направленных против внешнего магнитного поля и соответственно ослабляющих его. В парамагнетиках частицы хаотично ориентированы, вследствие чего суммарный магнитный момент будет равен нулю. При наложении внешнего магнитного поля, частицы вещества и их магнитные моменты упорядочиваются и ориентируются в направлении поля. Это в свою очередь приводит к усилению внешнего магнитного поля. Механизм намагничивания ферромагнетиков значительно сложней. Согласно гипотезы Вейса, вследствие наличия внутреннего молекулярного поля в состоянии полного размагничивания, ферромагнетики распадаются на большое число мельчайших областей спонтанного намагничивания, так называемых доменов. Если нет внешнего магнитного поля, то магнитные моменты доменов ориентированы в пространстве беспорядочно и хаотично, поэтому ферромагнетик в целом ненамагничен. Намагничивание ферромагнетиков во внешнем магнитном поле возникает вследствие переориентации векторов намагничивания доменов в направлении приложенного поля, которое включает в себя смещение, вращение и парапроцесс. При смещении нарушаются границы доменов и те домены, направление ориентации которых близко к направлению магнитного поля, увеличиваются за счёт тех доменов, которые энергетически являются менее выгодными. При этом нарастающие домены изменяют размеры, форму и энергию. Процесс вращения состоит в повороте вектора намагниченности домена 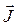в направлении поля. Поворот такого вектора осуществляется с затратой энергии внешнего магнитного поля. Парапроцесс состоит в увеличении абсолютного значения вектора спонтанной намагниченности под действием внешнего магнитного поля напряжённости 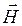. Парапроцесс наступает тогда, когда 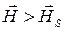и обусловлен ориентацией в поле напряжённостью 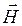элементарных носителей магнетизма (спиновых и орбитальных моментов), которые остались неориентированными вследствие теплового движения. Парапроцесс является завершающим этапом в намагничивании ферромагнетиков, но не определяющим. Ферромагнетики характеризуются гистерезисом, т.е. зависимостью его магнитных свойств от предыдущего магнитного состояния, а также характеризуются точкой Кюри – температурой, выше которой вещество утрачивает свои ферромагнитные свойства и ферромагнетик превращается в парамагнетик. Точка Кюри есть та критическая температура, переход через которую связан с фазовым переходом 2-го рода. В дальнейшем, с момента появления квантовой механики, гипотеза Вейса нашла своё обоснование. Согласно новейшим концепциям, для объяснения ферромагнетизма одних классических представлений оказалось мало. Как оказалось, природа спонтанной намагниченности крылась в наличии так называемых обменных сил, роль которых была определяющей. Действительно, в силу принципа тождественности частиц, атомы различных химических элементов могут обмениваться электронами без всяческих изменений. Энергия такого обмена носит название обменной энергии. При определённом строении электронных оболочек атомов, или особенностях строения кристаллической решётки, обменные силы стараются расположить спины электронов параллельно между собой, что в свою очередь и становится причиной спонтанного намагничивания ферромагнетиков.

2.2.4. Антиферромагнетики.

Антиферромагнетики представляют собой кристаллические вещества, в которых магнитные моменты атомов или ионов образуют две или несколько магнитных подрешёток, представляющих собой пространственные подсистемы, возникающие в магнетиках под влиянием возмущения и связанные с процессами упорядочения магнетиков. В антиферромагнетиках магнитные моменты обладают антипараллельной (в случае двух подрешёток) или более сложной пространственной ориентацией. Такая ориентация магнитных моментов указывает на отсутствие спонтанной намагниченности у вещества в целом. Во внешнем магнитном поле антиферромагнетики обладают небольшой намагниченностью. Характерная для антиферромагнетиков магнитная структура возникает при определённой температуре (точка Нееля) 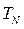и сохраняется ниже этой температуры. Выше этой температуры, наблюдается фазовый переход 2-го рода, и антиферромагнетик становится парамагнетиком. Изучение антиферромагнетиков позволило глубже понять свойства веществ со сложной магнитной структурой.

2.2.5. Ферримагнетики.

Ферримагнетики представляют собой материалы, у которых магнитные моменты атомов различных подрешёток ориентируются антипараллельно, как и в антиферромагнетиках, но моменты различных подрешёток не равны, и, тем самым, результирующий момент не равен нулю. Ферримагнетики характеризуются спонтанной намагниченностью. Различные подрешётки в них состоят из различных атомов или ионов. Свойствами ферримагнетиков обладают некоторые упорядоченные металлические сплавы, но, главным образом, различные оксидные соединения, среди которых наибольший практический интерес представляют ферриты. Ферримагнетики имеют доменную структуру, состоящую из двух и более подрешёток, связанных антиферромагнитно. Поскольку подрешётки образованы атомами или ионами различных химических элементов или неодинаковым их количеством, они имеют различные по величине магнитные моменты, направленные антипараллельно. В результате появляется отличная от нуля разность магнитных моментов подрешёток, приводящая к спонтанному намагничиванию кристалла. Таким образом, ферримагнетики можно рассматривать как нескомпенсированные антиферромагнетики. Своё название эти материалы получили от ферритов – первых некомпенсированных антиферромагнетиков, а магнетизм ферритов назвали ферримагнетизмом. У ферритов доменная структура, как и у ферромагнетиков, образуется при температурах ниже точки Кюри. К ферритам применимы все магнитные характеристики, введенные для ферромагнетиков. В отличие от ферромагнетиков, они имеют высокое значение удельного сопротивления, меньшую величину индукции насыщения, более сложную температурную зависимость индукции. Ферромагнетизм в металлах объясняется наличием обменного взаимодействия, которое образуется между соприкасающимися атомами, а также взаимной ориентацией спиновых магнитных моментов. В ферримагнетиках магнитные моменты ионов ориентированы антипараллельно, и обменное взаимодействие происходит не непосредственно, а опосредованно, через атомы или группы атомов. Такое обменное взаимодействие называют косвенным обменом или сверхобменом. Оно усиливается по мере приближения промежуточного угла от 0° к 180°.

2.3. Основные типы квазичастиц в магнетиках различных типов.

Поведение квантово-механической системы, состоящей из очень большого числа взаимодействующих частиц, квантово-механическая задача многих тел – одна из наиболее сложных задач современной физики. В этом направлении огромный прогресс был, достигнут на пути использования концепции квазичастиц, впервые введенной в 50-х годах XX в. Ландау при построении теории ферми-жидкости. В рамках развитых им концепций, все сложные взаимодействия, испытываемые исходной частицей, сохраняются в свойствах новых невзаимодействующих объектов, называемых квазичастицами. Развитие представлений о квазичастицах направлено на реализации одной цели – описание макроскопической системы в равновесии как ансамбль невзаимодействующих квазичастиц. Неравновесное поведение тогда будет описываться кинетической теорией этих частиц. Математически введение квазичастиц означает переход к новой системе квантов возбуждения, которые являются элементами диаганолизованного полного (включая взаимодействия) гамильтониана системы. В общем случае под квазичастицами понимают элементарное коллективное возбуждение или возмущение многочастичной системы, обладающей определённой энергией и, как правило, импульсом. Как и обычная частица, квазичастица может быть локализованной в пространстве и сохранять её в процессе движения. Квазичастицы могут взаимодействовать друг с другом и с обычными частицами, например, с фотонами. Для квазичастиц с квадратичным законом дисперсии, т.е. энергия пропорциональная квадрату импульса, можно ввести эффективную массу. Поведение такой квазичастицы будет очень похоже на поведение обычных частиц. В отличие от обычных частиц, квазичастицы не могут существовать вне среды, колебаниями которой они и являются. Рассмотрим основные типы квазичастиц, играющих существенную роль в транспортных свойствах передачи электронного возбудения в сильнокоррелированных низкоразмерных магнитоупорядоченных системах, возникновение которых обычно имеет место в конденсированных средах.

Экситон – водородоподобная квазичастица, представляющая собой электронное возбуждение в диэлектрике, полупроводнике или металле, мигрирующее по кристаллу или плёнке и не связанное с переносом заряда или массы. Хотя экситон состоит из электрона и «дырки», его следует считать самостоятельной частицей в случаях, когда энергия взаимодействия электрона и «дырки» имеет тот же порядок, что и энергия их движения, а энергия между двумя экситонами мала в сравнении энергией каждого из них в отдельности. Экситон можно считать элементарной квазичастицей в тех явлениях, в которых он выступает как целое образование, не подвергающееся воздействиям, способным его разрушить. Он может быть представлен в виде некоторого связанного состояния электрона проводимости и «дырки», расположенных или в одном узле кристаллической решётки (как в случае с экситоном Френкеля), или на расстояниях, значительно больше межатомных, например, экситон Ванье-Мотта. Последние могут быть только в полупроводниках, в то время как экситоны Френкеля могут быть в молекулярных кристаллах.

Солитон – структурно устойчивая уединённая волна, распространяющаяся в нелинейной среде. Солитоны ведут себя подобно частицам – при взаимодействии друг с другом или с некоторыми другими возмущениями, они не разрушаются, а движутся, сохраняя свою структуру неизменной. Это свойство может быть использовано для передачи данных на большие расстояния без помех.

Полярон – квазичастица в кристалле, состоящая из электрона и сопровождающего его поля поляризации. Медленно движущиеся электроны поляризации в кристалле диэлектрика взаимодействуют с ионами решётки, через дальнодействующие силы электрон при своём движении окружается областью решёточной поляризации и деформации, вызванной движением электрона. Двигаясь через кристалл или тонкую плёнку, электрон проводит решёточную деформацию, по этой причине оказывается возможным говорить о наличии облака фононов, которое сопровождает движущийся электрон. Размер полярона определяется соотношением между размером возмущённой области кристалла и постоянной кристалла.

Поляритон – составная квазичастица, возникающая при взаимодействии фотонов и элементарных возбуждений среды – фононы, экситоны, плазмоны, магноны.

2.4. Общая характеристика обменных сил, их роль в формировании упорядоченности магнетиков.

В ряде случаев, когда мы имеем дело с целым ансамблем электронов, оказывается необходимым учитывать как их электростатическое взаимодействие, так и взаимодействие, которое определяется наличием постоянно действующих между ними обменными силами:

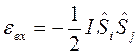
здесь 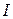– параметр обменного взаимодействия. Обменное взаимодействие зависит от взаимной ориентации спинов электронов. Так, если 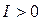, то обменное взаимодействие стремится ориентировать спины электронов параллельно друг другу. Обменное взаимодействие создаёт эффективное молекулярное поле, которое действует на электроны так же, как внешнее магнитное поле. Это в свою очередь приводит к тому, что создаваемое таким образом молекулярное поле изменяет энергии подзон со спинам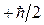и и 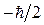, и в случае 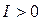электроны из подзоны 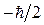переходят в подзону 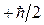. В общем случае в системе магнитных моментов в результате совместного действия ряда конкурирующих факторов формируется магнитное состояние. Различают обычно два возможных типа магнетизма – кооперативный и некооперативный магнетизм. В случае некооперативного магнетизма, магнитные моменты ведут себя независимо друг от друга, упорядочение таких магнитных систем создаётся магнитным полем. Под кооперативным магнетизмом обычно понимают упорядочение, возникающее вследствие магнитного взаимодействия. При этом магнитное поле служит средством обнаружения упорядочения на макроскопическом уровне. Взаимодействие магнитных моментов с позиции квантовой механики может быть описано несколькими способами, однако все они основаны на принципе тождественности частиц и принципе Паули, с позиций которых может быть показано возникновение так называемой обменной «дырки». Необходимо отметить, что основой всех обменных сил возникающих в магнетиках ферромагнитного, антиферромагнитного и ферримагнитного типов, является принцип Паули, который позволяет описать роль обменных сил и их воздействие на кулоновское отталкивание электронов. По иерархии обменных взаимодействий можно выделить прямой и непрямой обмен. Под прямым обменом понимают связь между квантовыми системами, расположенными так близко друг от друга, что происходит перекрывание волновых функций атомов, непосредственных партнёров по связи. В случае непрямого обмена, имеет место взаимодействие квантовых систем настолько удалённых друг от друга, что оказывается необходимым участие некоего посредника. При этом возможны два основных случая – взаимодействие РККИ и косвенное обменное взаимодействие. В первом случае обменное взаимодействие опосредуется за счёт электронов проводимости, в случае же косвенного обменного взаимодействия, последнее осуществляется за счёт лигандов. Эффективное электростатическое взаимодействие между частицами, в общем случае, зависит от относительной ориентации спинов. Такое взаимодействие удобно представить, как изотропное взаимодействие двух спинов, зависящее только от расстояния между ионами. Тогда если ионы i и j со спинам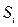и и расположены на расстоянии 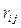, энергию обменного взаимодействия можно записать соответственно в виде:

где 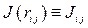– параметр обменного взаимодействия. При этом в зависимости от того, какой из типов обменного взаимодействия – прямое, косвенное или РККИ-взаимодействие имеют место в магнетике, сам параметр может принимать различные значения, отличаясь по знаку, имея в ряде случаев осциллирующий характер. Рассмотрим подробней РККИ-взаимодействие. Так, при движении по кристаллу или плёнке, электроны проводимости переносят взаимодействие между локализованными магнитными моментами. Локализованный магнитный момент поляризует облако окружающих его электронов. Эта поляризация является осциллирующей в пространстве. Электроны проводимости стремятся своими спинами заэкранировать магнитные моменты иона, однако, волновые функции электронов ограниченным числом длин волн (набором квантовых чисел). При этом максимальное значение волнового числа не может превышать 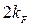. Неосциллирующая функция представляется через неполный набор Фурье-компонент, поэтому сохраняется остаточное осциллирующее поведение. В случае квадратичного закона дисперсии электронов, зависимость эффективного обменного интеграла от расстояния записывается в виде:

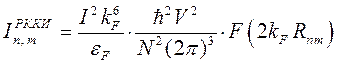
где

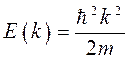
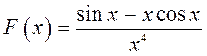
Функция Рудермана-Киттеля определяет зависимость обменного интеграла от расстояния 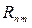между магнитными ионами. В зависимости от расстояния между магнитными ионами, обмен РККИ может быть ферромагнитным (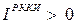) и антиферромагнитным (). На больших расстояниях осцилляции затухают:

Взаимодействие РККИ имеет большой радиус действия, является осциллирующим, и сильно зависит от концентрации свободных носителей заряда. Несмотря на явно информативный характер данного типа обменного взаимодействия, не имеющего непосредственного отношения к данной работе, тем не менее, на мой взгляд, общие сведения о так называемом знакопеременном обмене являются весьма полезными, поскольку позволяют объяснить существование различных магнитных структур, в частности, геликоидального упорядочения в магнетиках. Рассмотрим теперь вопросы, касающиеся упорядочения имеющие место в магнетиках. Так, с понижением температуры, в системе магнитных моментов, связанных обменным взаимодействием, произойдёт упорядочение магнитных моментов. В данном случае температура будет служить разупорядочивающим фактором, обменное взаимодействие – упорядочивающим фактором для магнитных подсистем, называемых также подрешётками. Здесь имеет место интересная особенность. Так, с одной стороны, внешнее магнитное поле служит неким упорядочивающим фактором и в то же самое время это же самое внешнее магнитное поле разрушает

упорядочение магнитной подрешётки, создаваемое обменными силами, т.е.

Для магнитных систем без взаимодействия бесспорно оказывается справедливым закон Кюри. С понижением температуры, как это хорошо видно из приведенного ниже выражения, магнитная воприимчивость системы возрастает:

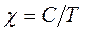
Если магнитные моменты системы связаны обменным взаимодействием, то для магнитной восприимчивости в области высоких температур (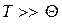) оказывается справедливым закон Кюри-Вейсса:

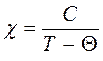
здесь 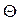– парамагнитная температура Кюри и – постоянная Кюри-Вейсса. Так, например, в системе магнитных моментов на магнитный момент иона действует эффективное обменное взаимодействие (электростатическое поле) – зависящее от взаимной ориентации магнитных моментов. Кроме того, в кристалле или плёнке на магнитный момент будет действовать ещё и эффективное кристаллическое поле, создаваемое окружающими ионами, являющееся также по своей природе электростатическим, что может быть описано на основании выражения вида:

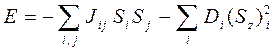
где 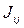– обменный интеграл, 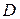– константа магнитной анизотропии. Локальное кристаллическое поле создаёт локальную ось лёгкого намагничивания, вдоль которой располагается магнитный момент. Обменное взаимодействие приводит к появлению некоторого эффективного обменного поля, которое ниже некоторой критической температуры 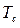преодолевает разупорядочивающее действие теплового движения. В результате при 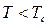возникает кооперативный эффект – магнитное упорядочивание магнитных моментов и как следствие – формирование магнитных подрешёток. При отсутствии внешнего магнитного поля магнитные моменты располагаются «правильным» образом. Классические системы с коллинеарным расположением магнитных моментов в низкотемпературной фазе – ферромагнетики и антиферромагнетики. В первом случае, когда классический магнетик в области низких температур проявляет ферромагнитные свойства, 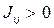– магнитные моменты параллельны между собой. Для случая антиферромагнитного упорядочения классического магнетика в области низких температур – 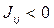, т.е. магнитные моменты будут располагаться антипараллельно. Необходимо сразу отметить, что наличие дальнего порядка в магнетиках, всегда гарантирует наличие и ближнего порядка и напротив, наличие ближнего порядка совсем не означает наличие дальнего упорядочения магнитных моментов. Ниже температуры Кюри 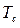, являющейся в данном случае критической температурой, сильно влияющей на свойства магнетиков – обменное взаимодействие преодолевает дезориентирующее действие теплового движения и ориентирует магнитные моменты параллельно друг другу. В результате в магнетике возникает так называемая спонтанная намагниченность 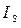, нарастающая при стремлении к пределу 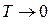. Наличие такой спонтанной намагниченности приводит в свою очередь к увеличению магнитостатической энергии магнетика. Минимизация этой энергии достигается за счёт того, что образец разбивается на домены, внутри которых есть спонтанная намагниченность вдоль одной из кристаллографических осей. Таким образом, в ходе проведенных рассуждений мы подошли к одному из важнейших понятий, лежащих в основе понимания физики магнитных явлений – домена. Рассмотрим доменную структуру ферромагнетиков. Так, энергия феромагнетика, связанная с обменом и энергия связанная с анизотропией свойств, как это было показано выше – зависят от величины намагниченности. В магнитоупорядоченном состоянии ферромагнетик представляет собой постоянный магнит, вокруг него существует магнитное поле, с которым связана энергия магнитодипольного взаимодействия, называемая также энергией размагничивающих полей. Реальная структурав ферромагнетика определяется конкуренцией всех выше приведенных взаимодействий. Эта конкуренция приводит к существованию доменов в реальных веществах. Доменная структура в общем случае является достатосчно чувствительной к внешнему магнитному полю. Так, ещё в 1907 г. Вейссом была предсказана доменная структура ферромагнетиков – каждый домен намагничен до насыщения, в соседних доменах намагниченности антипараллельрны, поэтому суммарная намагниченность образца меньше максимальной и может быть равна нулю. В 1932 г. Биттер, Хамос и Тиссен наблюдали доменную структуру ферромагнетиков в виде порошковых фигур в микроскоп. В том же году Юлох произвёл впервые расчёты доменной стенки и тремя годами позже (1935) Ландау и Лифшиц предложили количественную теорию доменов. Согласно современным представлениям, домены представляют однородно намагничены области магнетика, а сама доменная стенка имеет макроскопические размеры, которые в общем случае много больше межатомных расстояний. В 1970 г. в результате фундаментальных работ Л. Нееля было открыто явления антиферромагнитного и ферримагнитного упорядочения магнетиков. За работы и открытия касающиеся антиферромагнетизма и ферримагнетизма, которые повлекли за собой важные приложения в теории конденсированного состояниявещества Л. Неелю была присуждена Нобелевская премия. Так, в некоторых веществах в результате взаимодействия соседних атомов, их магнитные моменты ориентируются в противоположных направлениях. Кристаллическую решётку таких веществ можно рассматривать, как две проникающие друг в друга магнитные подрешётки, каждая из которых состоит из атомов с одинаково ориентироованными магнитными моментами. Ниже критической температуры (температура Нееля 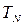) магнитные подрешётки взаимно компенсируют друг друга, давая нулевую суммарную намагниченность. В антиферромагнетике обменныые интегралы отрицательны, то есть каждый ион окружён ионами, с магнитными моментами, ориентированными противоположно его собственному моменту. Магнитная восприимчивость в области

высоких температур подчиняется закону Кюри-Вейсса с отрицательным значение 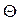. В точке температуры Нееля 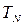– максимум восприимчивости. В области же низких температур поведение 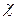анизотропно – вдоль одной из осей 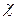падает до нуля, вдоль других направлений, напротив, остаётся величиной постоянной. Таким образом, имеем ограничение в двух направлениях. В общем случае за ориентацию суммарной намагниченности отвечают две составляющие: диполь-дипольное взаимодействие между магнитными моментами и спин-орбитальное взаимодействие. С антиферромагнетиками связаны очень интересные в энергетическом отношении явления, получившие название «спин-флоп» и «спин-флип» переходы. Данные явления, прежде всего, связаны с тем, что основное состояние антиферромагнетика представляет собой упорядоченную магнитную структуру, отделённую от возбуждённых состояний энергетической щелью. Возбуждение в антиферромагнетике состоит в том, что одна пара магнитных моментов «неправильно» ориентируется относительно других магнитных моментов. Так, поскольку антиферромагнетику свойственна анизотропия, то во внешнем магнитном поле его намагниченность будет меняться не непрерывно, а скачкообразно при непрерывном увеличении магнитного поля. Итак, как было выяснено, установление дальнего магнитного порядка в ферро- и антиферромагнетиках является кооперативным квантовым эффектом. Порядок в магнетиках такого типа формируется при температуре ниже критической. Установление порядка является фазовым переходом 2-го рода, в системе возникает параметр порядка – спонтанная намагниченность. Поведение магнитной восприимчивости в области высоких температур подчиняется закону Кюри-Вейсса. В упорядоченной области поведение магнитной восприимчивости и намагниченности для ферромагнетиков, принципиально отличаются от магнетиков антиферромагнитного типа. Для антиферромагнетика характерна анизотропия магнитной восприимчивости, следствием анизотропии свойств магнетиков такого типа является щель в спектре магнитных возбуждений – основное состояние отделено энергетической щелью, оно устойчиво к воздействию магнитного поля и температуры. Переход магнетика из своего основвного состояния в возбуждённое, осуществляется за счёт «спин-флоп» и «спин-флип» переходов, носящими характер фазовых переходов 2-го рода. Особую роль и внимание, в связи с выбранной тематикой работы, заслужтвает рассмотрение явления ферримагнетизма и обращение намагниченности, открытые в своё время Неелем. В общем случае, ферримагнетизм представляет собой особое магнитное состояние вещества, при котором элементарные магнитные моменты атомов или ионов входящих входящих в состав вещества, образуют две или большее число магнитных подрешёток. Каждая из таких подрешёток содержит атомы или ионы одного типа с одинаково ориентированными магнитными моментами. Магнитные моменты атомов или ионов различных подрешёток в общем случае направлены навстречу друг другу или, в более общем случае, образуют сложную пространственную конфигурацию, например лестничного или винтового типа. Достаточно часто число атомов или ионов в одлной подрешётке в кратное число раз больше, чем в другой. Ферримагнетизм можно рассматривать как наиболее общий случай упорядоченного состояния. Самопроизвольная намагниченность вещества в ферримагнитном состоянии в общем случае равна вектороной сумме намагниченностей всех подрешёток. В общем случае при высоких температурах, когда энергия теплового двтжения много больше обменной энергии (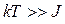), вещество обладает парамагнитными свойствами. Температурная зависимость магнитной восприимчивости 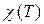веществ, в которых при низких температурах возникает ферримагнетизм, обладает характерными особенностями: 1.) при высоких температурах магнитная восприимчивость 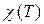таких веществ следует закону Кюри-Вейсса с отрицательной константой 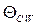; 2.) при понижении температуры магнитная восприимчивость 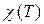ферримагнетика круто спадает, стремясь к нулю при 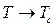; 3.) в точке Кюри 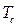, когда энергия обменного взаимодействия становится равной энергии теплового движения в веществе, возникает ферримагнитное упорядочение. В большинстве случаев переход 2-го рода сопровождается характерными аномалиями теплоёмкости, линейного расширения. С понижением температуры квантовомеханическая система занимает наиболее энергетически выгодное, максимально упорядоченное основвное состояние. Энтропия системы убывает по мере уменьшения температуры. Способы формирования основного состояния могут быть самыми различными и осуществляться как посредством фазовых превращений, так и без помощи таковых. Как было сказано уже ранее в предыдущем разделе, температура здесь играет роль разупорядочивающего фактора. Магнитное же поле напротив, упорядочивает магнитную систему, приводя к формированию магнитных подрешёток. Классическим случаем установления магнитного порядка в твёрдом теле является ферромагнитный или антиферромагнитный дальний порядок, спонтанно возникающий в 3D системе взаимодействующих ионов или атомов с локализованным магнитным моментом при понижении температуры. Установлено, что основное состояние в случае ферромагнетизма является бесщелевым, а в случае антиферромагнетизма, напротив, основное состояние отдел