Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Спектр.

Спектр линейного ограниченного оператора

Пусть 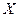- комплексное банахово пространство, 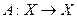- линейный ограниченный оператор. Рассмотрим линейный ограниченный оператор 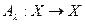, зависящий от параметра ,

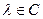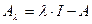, или

.

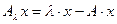Определение 1. Значение 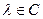называется регулярным значением оператора 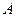, если соответствующий этому значению оператор 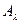обратим, т. е. существует линейный ограниченный оператор .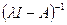

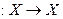Множество всех регулярных значений оператора называется резольвентным и обозначается 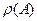. Это множество объединяет только те значения параметра 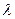, при которых оператор 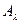является (непрерывно) обратимым.

Определение 2. Спектром 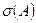оператора 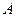называется множество всех тех 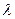, для которых оператор 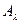не имеет ограниченного обратного.

Таким образом, комплексная плоскость 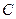представляется в виде дизъюнктивного объединения резольвентного множества и спектра оператора 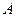, т.е.

.

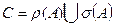Рассмотрим основные свойства спектра и резольвентного множества.

Теорема 1. Резольвентное множеств линейного ограниченного оператора 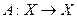является открытым неограниченным множеством.

Доказательство. Сначала докажем, что 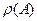- неограниченное множество. Произвольно зафиксируем 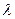такое, что 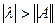. Докажем, что соответствующий оператор 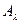= 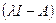обратим. Это и будет означать, что значение 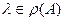), а, следовательно, 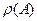- неограниченное множество.

Полагая, что 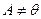, имеем 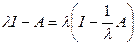. Обратимость этого оператора следует из выполнения условия 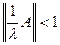или 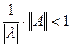(теорема 3 об обратимости).

Для доказательства открытости зафиксируем 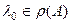и покажем что 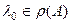вместе с некоторой своей окрестностью. Это и означает открытость множества .

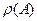Пусть 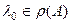и рассмотрим равенство

,

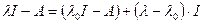в котором первое слагаемое является обратимым оператором по предположению. Сумма операторов является обратимым оператором по теореме 4, если норма второго слагаемого удовлетворяет неравенству:

,

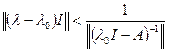Так как 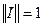, то при 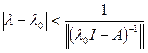оператор 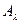обратим. Следовательно, резольвентное множество 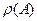является открытым. Теорема доказана.

Теорема 2. Спектр 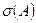любого ограниченного линейного оператора является: непустым, замкнутым и ограниченным множеством.

Доказательство. Доказательство того, что 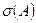- непустое множество опустим. Напомним, что спектр является дополнением резольвенты до всей комплексной плоскости. Поэтому замкнутость 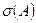следует из того, что 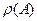- открытое множество. Следовательно, дополнение 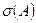открытого множества 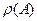является замкнутым.

Из доказательства теоремы 1 следует, что спектр 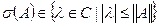(кругу радиуса равного 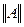). Следовательно, спектр ограниченное множество. Теорема доказана.

В зависимости от причины необратимости оператора 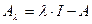спектр подразделяется на три взаимно непересекающихся подмножества. Для нас интерес представляет подмножество 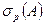, называемое точечным спектром оператора 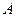. Точечный спектр содержит только те значения 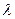, при которых ядро оператора 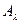нетривиально, т.е. 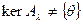. При этом уравнение 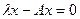имеет хотя бы одно ненулевое решение. Такое значение 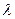называется собственным, а соответствующие элементы собственными. Таким образом, точечный спектр объединяет все собственные значения данного оператора.

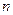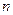Для вполне непрерывных операторов спектр имеет достаточно простую структуру, аналогично структуре спектра матричного оператора. Напомним, что спектр матричного оператора в - мерном евклидовом пространстве содержит только собственных значений с учетом их кратности, то есть ).

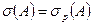Теорема 3. Спектр вполне непрерывного ограниченного оператора содержит не более чем счетное множество собственных значений с единственно возможной предельной точкой 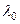=0.

Утверждение теоремы 3 можно записать в виде 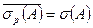.