💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 18 страница

Рассмотрение структуры и особенностей характеристических рентгеновских спек­тров приводит к выводу, что их возникновение связано с процессами, происходящими во внутренних, застроенных электронных оболочках атомов, которые имеют сходное строение.

Разберем механизм возникновения рентгеновских серий, который схематически показан на рис. 307. Предположим, что под влиянием внешнего электрона или высокоэнергетического фотона вырывается один из двух электронов K -оболочки атома. Тогда на его место может перейти электрон с более удаленных от ядра оболочек L, M, N,.... Такие переходы сопровождаются испусканием рентгеновских квантов и возникновени­ем спектральных линий К- серии: К_a (L ® K), K_b (M ® K), K_g (N ® K) и т. д. Самой длинно­волновой линией К- серии является линия K_a. Частоты линий возрастают в ряду K_a ® K_b ® K_g, поскольку энергия, высвобождаемая при переходе электрона на K -оболочку с более удаленных оболочек, увеличивается. Наоборот, интенсивности линий в ряду K_a ® K_b ® K_g убывают, так как вероятность переходов электронов с L -оболочки на K -оболочку больше, чем с более удаленных оболочек М и N. К- серия сопровождается обязательно другими сериями, так как при испускании ее линий появляются вакансии в оболочках L, M,..., которые будут заполняться электронами, находящимися на более высоких уровнях.

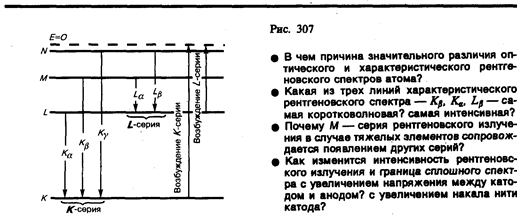
Аналогично возникают и другие серии, наблюдаемые, впрочем, только для тяже­лых элементов. Рассмотренные линии характеристического излучения могут иметь тонкую структуру, поскольку уровни, определяемые главным квантовым числом, расщепляются согласно значениям орбитального и магнитного квантовых чисел.

Исследуя рентгеновские спектры элементов, английский физик Г. Мозли (1887—1915) установил в 1913 г. соотношение, называемое законом Мозли:

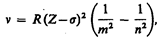(229.2)

где n — частота, соответствующая данной линии характеристического рентгеновского излучения, R — постоянная Ридберга, s — постоянная экранирования, т = 1, 2, 3,... (определяет рентгеновскую серию), n принимает целочисленные значения начиная с m +1 (определяет отдельную линию соответствующей серии). Закон Мозли (229.2) подобен обобщенной формуле Бальмера (209.3) для атома водорода.

Смысл постоянной экранирования заключается в том, что на электрон, совершающий переход, соответствующий некоторой линии, действует не весь заряд ядра Zе, а заряд (Z – s) e, ослабленный экранирующим действием других электронов. Напри­мер, для K_a -линии s = 1, и закон Мозли запишется в виде

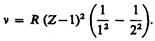
§ 230. Молекулы: химические связи, понятие об энергетических уровнях

Молекула — наименьшая частица вещества, состоящая из одинаковых или различных атомов, соединенных между собой химическими связями, и являющаяся носителем его основных химических и физических свойств. Химические связи обусловлены взаимодей­ствием внешних, валентных электронов атомов. Наиболее часто в молекулах встреча­ется два типа связи: ионная и ковалентная (см. § 71).

Ионная связь (например, в молекулах NaCl, KBr) осуществляется электростатичес­ким взаимодействием атомов при переходе электрона одного атома к другому, т. е. при образовании положительного и отрицательного ионов. Ковалентная связь (напри­мер, в молекулах H₂, С₂, СО) осуществляется при обобществлении валентных элек­тронов двумя соседними атомами (спины валентных электронов должны быть ан­типараллельны). Ковалентная связь объясняется на основе принципа неразличимости тождественных частиц (см. § 226), например электронов в молекуле водорода. Нераз­личимость частиц приводит к специфическому взаимодействию между ними, называ­емому обменным взаимодействием. Это чисто квантовый эффект, не имеющий клас­сического объяснения, но его можно себе представить так, что электрон каждого из атомов молекулы водорода проводит некоторое время у ядра другого атома и, следовательно, осуществляется связь обоих атомов, образующих молекулу. При сбли­жении двух водородных атомов до расстояний порядка боровского радиуса возникает их взаимное притяжение и образуется устойчивая молекула водорода.

Молекула является квантовой системой; она описывается уравнением Шредингера, учитывающим движение электронов в молекуле, колебания атомов молекулы, враще­ние молекулы. Решение этого уравнения — очень сложная задача, которая обычно разбивается на две: для электронов и ядер.

Энергия изолированной молекулы

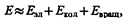(230.1)

где Е _эл — энергия движения электронов относительно ядер, Е _кол — энергия колебаний ядер (в результате которых периодически изменяется относительное положение ядер), Е _вращ — энергия вращения ядер (в результате которых периодически изменяется ориен­тация молекулы в пространстве). В формуле (230.1) не учтены энергия поступательного движения центра масс молекулы и энергия ядер атомов в молекуле. Первая из них не квантуется, поэтому ее изменения не могут привести к возникновению молекулярного спектра, а вторую можно не учитывать, если не рассматривать сверхтонкую структуру спектральных линий. Отношения Е _эл: Е _кол: Е _вращ = 1: 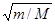: т/М, где т — масса электрона, М — величина, имеющая порядок массы ядер атомов в молекуле, т/М»10^–5¸ 10^–3. Поэтому Е _эл > > Е _кол > > Е _вращ. Доказано, что Е _эл»1¸ 10 эВ, Е _кол»10^–2¸ 10^–1 эВ, Е _вращ»10^–5¸ 10^–3эВ.

Каждая из входящих в выражение (230.1) энергий квантуется (ей соответствует набор дискретных уровней энергии) и определяется квантовыми числами. При переходе из одного энергетического состояния в другое поглощается или испускается энергия D E = hn. При таких переходах одновременно изменяются энергия движения электронов, энергии колебаний н вращения. Из теории и эксперимента следует, что расстояние между вращательными уровнями энергии D E _вращ гораздо меньше расстояния между колебательными уровнями D E _кол которое, в свою очередь, меньше расстояния между электронными уровнями D E _эл. На рис. 308 схематически представлены уровни энергии двухатомной молекулы (для примера рассмотрены только два электронных уров­ня — показаны жирными линиями).

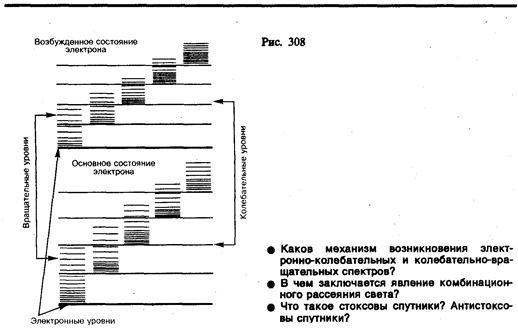
Как будет показано в § 231, структура энергетических уровней молекул определяет их спектр излучения, возникающий при квантовых переходах между соответствующи­ми энергетическими уровнями.

§ 231. Молекулярные спектры. Комбинационное рассеяние света

Строение молекул и свойства их энергетических уровней проявляются в молекулярных спектрах — спектрах излучения (поглощения), возникающих при квантовых переходах между уровнями энергии молекул. Спектр излучения молекулы определяется струк­турой ее энергетических уровней и соответствующими правилами отбора (так, напри­мер, изменение квантовых чисел, соответствующих как колебательному, так и враща­тельному движению, должно быть равно ± 1).

Итак, при разных типах переходов между уровнями возникают различные типы молекулярных спектров. Частоты спектральных линий, испускаемых молекулами, мо­гут соответствовать переходам с одного электронного уровня на другой (электронные спектры) или с одного колебательного (вращательного) уровня на другой (колебатель­ные (вращательные) спектры). Кроме того, возможны и переходы с одними значениями D E _кол и D E _вращ на уровни, имеющие другие значения всех трех компонентов, в результате чего возникают электронно-колебательные и колебательно-вращательные спектры. По­этому спектр молекул довольно сложный.

Типичные молекулярные спектры — полосатые, представляющие собой совокуп­ность более или менее узких полос в ультрафиолетовой, видимой и инфракрасной областях. Применяя спектральные приборы высокой разрешающей способности, можно видеть, что полосы представляют собой настолько тесно расположенные линии, что они с трудом разрешаются. Структура молекулярных спектров различна для разных молекул и с увеличением числа атомов в молекуле усложняется (наблюдаются лишь сплошные широкие полосы). Колебательными и вращательными спектрами обладают только многоатомные молекулы, а двухатомные их не имеют. Это объясняется тем, что двухатомные молекулы не имеют дипольных моментов (при колебательных и вра­щательных переходах отсутствует изменение дипольного момента, что является необ­ходимым условием отличия от нуля вероятности перехода).

В 1928 г. академики Г. С. Ландсберг (1890—1957) и Л. И. Мандельштам и одно­временно индийские физики Ч. Раман (1888—1970) и К. Кришнан (р. 1911) открыли явление комбинационного рассеяния света. Если на вещество (газ, жидкость, прозрачный кристалл) падает строго монохроматический свет, то в спектре рассеянного света помимо несмещенной спектральной линии обнаруживаются новые линии, частоты которых представляют собой суммы или разности частоты n падающего света и частот n_i собственных колебаний (или вращений) молекул рассеивающей среды.

Линии в спектре комбинационного рассеяния с частотами n – n_i, меньшими частоты n падающего света, называются стоксовыми (или красными) спутниками, линии с часто­тами n + n_i, большими n, — антистоксовыми (или фиолетовыми) спутниками. Анализ спектров комбинационного рассеяния приводит к следующим выводам: 1) линии спутников располагаются симметрично по обе стороны от несмещенной линии; 2) ча­стоты n_i не зависят от частоты падающего на вещество света, а определяются только рассеивающим веществом, т. е. характеризуют его состав и структуру; 3) число спут­ников определяется рассеивающим веществом; 4) интенсивность антистоксовых спут­ников меньше интенсивности стоксовых и с повышением температуры рассеивающего вещества увеличивается, в то время как интенсивность стоксовых спутников практичес­ки от температуры не зависит.

Объяснение закономерностей комбинационного рассеяния света дает квантовая теория. Согласно этой теории, рассеяние света есть процесс, в котором один фотон поглощается и один фотон испускается молекулой. Если энергии фотонов одинаковы, то в рассеянном свете наблюдается несмещенная линия. Однако возможны процессы рассеяния, при которых энергии поглощенного и испущенного фотонов различны. Различие энергии фотонов связано с переходом молекулы из нормального состояния в возбужденное (испущенный фотон будет иметь меньшую частоту — возникает стоксов спутник) либо из возбужденного состояния в нормальное (испущенный фотон будет иметь большую частоту — возникает антистоксов спутник).

Рассеяние света сопровождается переходами молекулы между различными колеба­тельными или вращательными уровнями, в результате чего и возникает ряд симмет­рично расположенных спутников. Число спутников, таким образом, определяется энергетическим спектром молекул, т. е. зависит только от природы рассеивающего вещества. Так как число возбужденных молекул гораздо меньше, чем число невозбуж­денных, то интенсивность антистоксовых спутников меньше, чем стоксовых. С повыше­нием температуры число возбужденных молекул растет, в результате чего возрастает и интенсивность антистоксовых спутников.

Молекулярные спектры (в том числе и спектры комбинационного рассеяния света) применяются для исследования строения и свойств молекул, используются в молеку­лярном спектральном анализе, лазерной спектроскопии, квантовой электронике и т. д.

§ 232. Поглощение. Спонтанное и вынужденное излучения

Как отмечалось выше, атомы могут находиться лишь в квантовых состояниях с дискрет­ными значениями энергии Е ₁, Е ₂, Е ₃ ,... Ради простоты рассмотрим только два из этих состояний (1 и 2) с энергиями Е ₁ и Е ₂. Если атом находится в основном состоянии 1, то под действием внешнего излучения может осуществиться вынужденный переход в воз­бужденное состояние 2 (рис. 309, а), приводящий к поглощению излучения. Вероят­ность подобных переходов пропорциональна плотности излучения, вызывающего эти переходы.

Атом, находясь в возбужденном состоянии 2, может через некоторый промежуток времени спонтанно, без каких-либо внешних воздействий, перейти в состояние с низшей энергией (в нашем случае в основное), отдавая избыточную энергию в виде электромаг­нитного излучения (испуская фотон с энергией hn=E ₂ –Е ₁). Процесс испускания фотона возбужденным атомом (возбужденной микросистемой) без каких-либо внешних воз­действий называется спонтанным (или самопроизвольным) излучением (рис. 309, б). Чем больше вероятность спонтанных переходов, тем меньше среднее время жизни атома в возбужденном состоянии. Так как спонтанные переходы взаимно не связаны, то спонтанное излучение некогерентно.

В 1916 г. А. Эйнштейн для объяснения наблюдавшегося на опыте термодинамичес­кого равновесия между веществом и испускаемым и поглощаемым им излучением постулировал, что помимо поглощения и спонтанного излучения должен существовать третий, качественно иной тип взаимодействия. Если на атом, находящийся в возбуж­денном состоянии 2, действует внешнее излучение с частотой, удовлетворяющей усло­вию hv=E ₂ –E ₁, то возникает вынужденный (индуцированный) переход в основное состояние 1 с излучением фотона той же энергии hv=E ₂ –E ₁ (рис. 309, в). При подобном переходе происходит излучение атомом фотона, дополнительно к тому фотону, под действием которого произошел переход. Возникающее в результате таких переходов излучение называется вынужденным (индуцированным) излучением. Таким образом, в процесс вынужденного излучения вовлечены два фотона: первичный фотон, вызыва­ющий испускание излучения возбужденным атомом, и вторичный фотон, испущенный атомом. Существенно, что вторичные фотоны неотличимы от первичных, являясь точной их копией.

В статистической физике известен принцип детального равновесия, согласно которо­му при термодинамическом равновесии каждому процессу можно сопоставить обрат­ный процесс, причем скорости их протекания одинаковы. А. Эйнштейн применил этот принцип и закон сохранения энергии при рассмотрении излучения и поглощения электромагнитных волн в случае черного тела. Из условия, что при равновесии полная вероятность испускания (спонтанного и вынужденного) фотонов равна вероятности поглощения фотонов той же частоты, Эйнштейн получил выведенную ранее Планком формулу (200.3).

Эйнштейн и Дирак показали, что вынужденное излучение (вторичные фотоны) тождественно вынуждающему излучению (первичным фотонам): оно имеет такие же частоту, фазу, поляризацию и направление распространения, как и вынуждающее излучение. Следовательно, вынужденное излучение строго когерентно с вынуждающим излучением, т. е. испущенный фотон неотличим от фотона, падающего на атом.

Испущенные фотоны, двигаясь в одном направлении и встречая другие возбужден­ные атомы, стимулируют дальнейшие индуцированные переходы, и число фотонов растет лавинообразно. Однако наряду с вынужденным излучением возможен и кон­курирующий процесс — поглощение. Поэтому для усиления падающего излучения необходимо, чтобы число актов вынужденного излучения фотонов (оно пропорци­онально заселенности возбужденных состояний) превышало число актов поглощения фотонов (оно пропорционально заселенности основных состояний). В системе атомов, находящейся в термодинамическом равновесии, поглощение падающего излучения будет преобладать над вынужденным, т. е. падающее излучение при прохождении через вещество будет ослабляться.

Чтобы среда усиливала падающее на нее излучение, необходимо создать неравновесное состояние системы, при котором число атомов в возбужденных состояниях было бы больше, чем их число в основном состоянии. Такие состояния называются состояниями с инверсией населенностей. Процесс создания неравновесного состояния вещества (перевод системы в состояние с инверсией населенностей) называется накачкой. Накачку можно осуществить оптическими, электрическими и другими способами.

В средах с инверсными состоящими вынужденное излучение может превысить поглощение, вследствие чего падающий пучок света при прохождении через эти среды будет усиливаться (эти среды называются активными). В данном случае явление протекает так, как если бы в законе Бугера I=I ₀ e^–ax (см. (187.1)) коэффициент поглощения a, зависящий, в свою очередь, от интенсивности излучения, стал от­рицательным. Активные среды поэтому можно рассматривать в качестве сред с от­рицательным коэффициентом поглощения.

Впервые на возможность получения сред, в которых свет может усиливаться за счет вынужденного излучения, указал в 1939 г. российский физик В. А. Фабрикант, экс­периментально обнаружив вынужденное излучение паров ртути, возбужденных при электрическом разряде. Открытие явления усиления электромагнитных волн и изоб­ретенный способ их усиления (В. А. Фабрикант, М. М. Вудынский, ф. А. Бугаева; 1951) легли в основу квантовой электроники, положения которой позволили впоследст­вии осуществить квантовые усилители и квантовые генераторы света.

§ 233. Оптические квантовые генераторы (лазеры)

Практически инверсное состояние среды осуществлено в принципиально новых источ­никах излучения — оптических квантовых генераторах, или лазерах (от первых букв английского названия Light Amplification by Stimulated Emission of Radiation — усиление света с помощью вынужденного излучения). Лазеры генерируют в видимой, инфракрасной и ближней ультрафиолетовой областях (в оптическом диапазоне). Идея качественно нового принципа усиления и генерации электромагнитных волн, применен­ная в мазерах (генераторы и усилители, работающие в сантиметровом диапазоне радиоволн) и лазерах, принадлежит российским ученым Н. Г. Басову (р. 1922) и А. М. Прохорову (р. 1916) и американскому физику Ч. Таунсу (р. 1915), удостоен­ным Нобелевской премии 1964 г.

Важнейшими из существующих типов лазеров являются твердотельные, газовые, полупроводниковые и жидкостные (в основу такого деления положен тип активной среды). Более точная классификация учитывает также и методы накачки — оптические, тепловые, химические, электроионизационные и др. Кроме того, необходимо прини­мать во внимание и режим генерации — непрерывный или импульсный.

Лазер обязательно имеет три основных компонента: 1) активную среду, в которой создаются состояния с инверсией населенностей; 2) систему накачки (устройство для создания инверсии в активной среде); 3) оптический резонатор (устройство, выделя­ющее в пространство избирательное направление пучка фотонов и формирующее выходящий световой пучок).

Первым твердотельным лазером (1960; США), работающим в видимой области спектра (длина волны излучения 0, 6943 мкм), был рубиновый лазер (Т. Мейман (р. 1927)). В нем инверсная населенность уровней осуществляется по трехуровневой схеме, предложенной в 1955 г. Н. Г. Басовым и А. М. Прохоровым. Кристалл рубина представляет собой оксид алюминия Аl₂О₃, в кристаллической решетке которого некоторые из атомов Аl замещены трехвалентными ионами Cr³⁺ (0, 03 и 0, 05% ионов хрома соответственно для розового и красного рубина). Для оптической накачки используется импульсная газоразрядная лампа. При интенсивном облучении рубина светом мощной импульсной лампы атомы хрома переходят с нижнего уровня 1 на уровни широкой полосы 3 (рис. 310). Так как время жизни атомов хрома в возбужден­ных состояниях мало (меньше 10^–7 с), то осуществляются либо спонтанные переходы 3 ® 1 (они незначительны), либо наиболее вероятные безызлучательные переходы на уровень 2 (он называется метастабильным) с передачей избытка энергии решетке кристалла рубина. Переход 2 ® 1 запрещен правилами отбора, поэтому длительность возбужденного состояния 2 атомов хрома порядка 10^–3 с, т. е. примерно на четыре порядка больше, чем для состояния 3. Это приводит к «накоплению» атомов хрома на уровне 2. При достаточной мощности накачки их концентрация на уровне 2 будет гораздо больше, чем на уровне 1, т. е. возникает среда с инверсной населенностью уровня 2.

Каждый фотон, случайно родившийся при спонтанных переходах, в принципе может инициировать (порождать) в активной среде множество вынужденных перехо­дов 2 ® 1, в результате чего появляется лавина вторичных фотонов, являющихся копиями первичных. Таким образом и зарождается лазерная генерация. Однако спон­танные переходы носят случайный характер, и спонтанно рождающиеся фотоны ис­пускаются в разных направлениях. Тем самым в самых разных направлениях распрост­раняются и лавины вторичных фотонов. Следовательно, излучение, состоящее из подобных лавин, не может обладать высокими когерентными свойствами.

Для выделения направления лазерной генерации используется принципиально важ­ный элемент лазера — оптический резонатор. В простейшем случае им служит пара обращенных друг к другу параллельных (или вогнутых) зеркал на общей оптической оси, между которыми помещается активная среда (кристалл или кювета с газом). Как правило, зеркала изготовляются так, что от одного из них излучение полностью отражается, а второе — полупрозрачно. Фотоны, движущиеся под углами к оси кри­сталла или кюветы, выходят из активной среды через ее боковую поверхность. Те же из фотонов, которые движутся вдоль оси, многократно отразятся от противоположных торцов, каждый раз вызывая вынужденное испускание вторичных фотонов, которые, в свою очередь, вызовут вынужденное излучение, и т. д. Так как фотоны, возникшие при вынужденном излучении, движутся в том же направлении, что и первичные, то поток фотонов, параллельный оси кристалла или кюветы, будет лавинообразно нара­стать. Многократно усиленный поток фотонов выходит через полупрозрачное зеркало, создавая строго направленный световой пучок огромной яркости. Таким образом, оптический резонатор «выясняет» направление (вдоль оси) усаливаемого фотонного потока, формируя тем самым лазерное излучение с высокими когерентными свойствами. Первым газовым лазером непрерывного действия (1961) был лазер на смеси атомов неона и гелия. Газы обладают узкими линиями поглощения, лампы же излучают свет в широком интервале длин волн; следовательно, применять их в качестве накачки невыгодно, так какиспользуется только часть мощности лампы. Поэтому в газовых лазерах инверсная населенность уровней осуществляется электрическим разрядом, возбуждаемым в газах.

В гелий-неоновом лазере накачка происходит в два этапа: гелий служит носителем энергии возбуждения, а неон дает лазерное излучение. Электроны, образующиеся в разряде, при столкновениях возбуждают атомы гелия, которые переходят в возбуж­денное состояние 3 (рис. 311). При столкновениях возбужденных атомов гелия с атома­ми неона происходит их возбуждение и они переходят на один из верхних уровней неона, который расположен вблизи соответствующего уровня гелия. Переход атома неона с верхнего уровня 3 на один из нижних уровней 2 приводит к лазерному излучению с l=0, 6328 мкм.

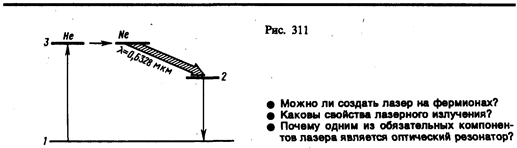
Лазерное излучение обладает следующими свойствами:

1. Временная и пространственная когерентность (см. § 171). Время когерентности составляет 10^–3 с, что соответствует длине когерентности порядка 10⁵ м (l _ког = сt _ког), т. е. на семь порядков выше, чем для обычных источников света.

2. Строгая монохроматичность (D l< 10^–11 м).

3. Большая плотность потока энергии. Если, например, рубиновый стержень при накачке получил энергию W= 20 Дж и высветился за 10^–3 с, то поток излучения Ф _е =20/10^–3 Дж/с=2× 10⁴ Вт. Фокусируя это излучение на площади 1 мм², получим плотность потока энергии Ф _е/S = 2× 10⁴/10^–6 Вт/м² = 2× 10¹⁰ Вт/м².

4. Очень малое угловое расхождение в пучке. Например, при использовании специ­альной фокусировки луч лазера, направленный с Земли, дал бы на поверхности Луны световое пятно диаметром примерно 3 км (луч прожектора осветил бы поверхность диаметром примерно 40 000 км).

К.п.д. лазеров колеблется в широких пределах — от 0, 01% (для гелий-неонового лазера) до 75% (для лазера на стекле с неодимом), хотя у большинства лазеров к.п.д. составляет 0, 1—1%. Создан мощный СО₂-лазер непрерывного действия, генериру­ющий инфракрасное излучение (l=10, 6 мкм), к.п.д. которого (30%) превосходит к.п.д. существующих лазеров, работающих при комнатной температуре.

Необычные свойства лазерного излучения находят в настоящее время широкое применение.

Применение лазеров для обработки, резания и микросварки твердых материалов оказывается экономически более выгодным (например, пробивание калиброванных отверстий в алмазе лазерным лучом сократило время с 24 ч до 6—8 мин). Лазеры применяются для скоростного и точного обнаружения дефектов в изделиях, для тончайших операций (например, луч СО₂-лазера в качестве бескровного хирургического ножа), для исследования механизма химических реакций и влияния на их ход, для получения сверхчистых веществ. Широко применяется лазерное разделение изотопов, например такого важного в энергетическом отношении элемента, как уран.

Одним из важных применений лазеров является получение и исследование высоко­температурной плазмы. Эта область их применения связана с развитием нового направления — лазерного управляемого термоядерного синтеза.

Лазеры широко применяются в измерительной технике. Лазерные интерферометры (в них источником света служит лазер) используются для сверхточных дистанционных измерений линейных перемещений, коэффициентов преломления среды, давления, тем­пературы. Например, рассмотренный выше гелий-неоновый лазер из-за излучения высокой стабильности, направленности и монохроматичности (полоса частот 1 Гц при частоте 10¹⁴ Гц) незаменим при юстировочных и нивелировочных работах.

Интересное применение лазеры нашли в топографии (см. § 184). Для создания систем голографической памяти с высокой степенью считывания и большой емкостью необходимы газовые лазеры видимого диапазона еще более высокой монохроматич­ности и направленности излучения.

Очень перспективны и интересны полупроводниковые лазеры, так как они облада­ют широким рабочим диапазоном (0, 7—30 мкм) и возможностью плавной перестрой­ки частоты их излучения.

Применения лазеров в настоящее время столь обширны, что даже их перечисление в объеме настоящего курса просто невозможно.

Глава 30Элементы квантовой статистики

§ 234. Квантовая статистика. Фазовое пространство. Функция распределения

Квантовая статистика — раздал статистической физики, исследующий системы, кото­рые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.

В отличие от исходных положений классической статистической физики, в которой тождественные частицы различимы (частицу можно отличить от всех таких же частиц), квантовая статистика основывается на принципе неразличимости тождественных ча­стиц (см. § 226). При этом оказывается, как будет показано ниже, что коллективы частиц с целым и полуцелым спинами подчиняются разным статистикам.

Пусть система состоит из N частиц. Введем в рассмотрение многомерное простран­ство всех координат и импульсов частиц системы. Тогда состояние системы определя­ется заданием 6 N переменных, так как состояние каждой частицы определяется трой­кой координат х, у, z и тройкой соответствующих проекций импульса р_х, р_у, p_z. Соответственно число «взаимно перпендикулярных» координатных осей данного про­странства равно 6 N. Это 6 N -мерное пространство называется фазовым пространством. Каждому микросостоянию системы отвечает точка в 6 N -мерном фазовом пространст­ве, так как задание точки фазового пространства означает задание координат и им­пульсов всех частиц системы. Разобьем фазовое пространство на малые 6 N -мерные элементарные ячейки объемом dqdp=dq ₁ dq ₂ ...dq _{3 N} dp ₁ dp ₂ ...dp _{3 N} , где q — совокупность координат всех частиц, р — совокупность проекций их импульсов. Корпускулярно-волновой дуализм свойств вещества (см. § 213) и соотношение неопределенностей Гейзенберга (см. § 215) приводят к выводу, что объем элементарной ячейки (он называется фазовым объемом) не может быть меньше чем h ³(h — постоянная Планка).