
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 3 страница
|
|
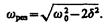 (148.1)
(148.1)
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При 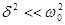 значение w рез практически совпадает с собственной частотой w 0 колебательной системы. Подставляя (148.1) в формулу (147.8), получим
значение w рез практически совпадает с собственной частотой w 0 колебательной системы. Подставляя (148.1) в формулу (147.8), получим
 (148.2)
(148.2)
На рис. 210 приведены зависимости амплитуды вынужденных колебаний от частоты при различных значениях d. Из (148.1) и (148.2) вытекает, что чем меньше d, тем выше и правее лежит максимум данной кривой. Если w ® 0, то все кривые (см. также (147.8)) достигают одного в того же, отличного от нуля, предельного значения  , которое называют статическим отклонением. В случае механических колебаний
, которое называют статическим отклонением. В случае механических колебаний  , в случае электромагнитных – U m / (L
, в случае электромагнитных – U m / (L 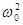 ). Если w ®¥, то вое кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.
). Если w ®¥, то вое кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.

Из формулы (148.2) вытекает, что при малом затухании (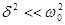 ) резонансная амплитуда смещения (заряда)
) резонансная амплитуда смещения (заряда)
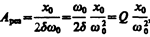
где Q — добротность колебательной системы (см. (146.8)),  — рассмотренное выше статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше А рез.
— рассмотренное выше статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше А рез.
На рис. 211 представлены резонансные кривые для амплитуды скорости (тока). Амплитуда скорости (тока)
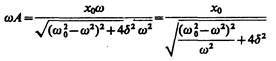
максимальна при w рез =w 0 и равна 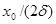 , т. е. чем больше коэффициент затухания d, тем ниже максимум резонансной кривой. Используя формулы (142.2), (146.10) и (143.4), (146.11), получим, что амплитуда скорости при механическом резонансе равна
, т. е. чем больше коэффициент затухания d, тем ниже максимум резонансной кривой. Используя формулы (142.2), (146.10) и (143.4), (146.11), получим, что амплитуда скорости при механическом резонансе равна
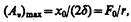
а амплитуда тока при электрическом резонансе
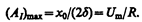
Из выражения tg j =  (см. (147.9)) следует, что если затухание в системе отсутствует (d= 0), то только в этом случае колебания и вынуждающая сила (приложенное переменное напряжение) имеют одинаковые фазы; во всех других случаях j ¹ 0.
(см. (147.9)) следует, что если затухание в системе отсутствует (d= 0), то только в этом случае колебания и вынуждающая сила (приложенное переменное напряжение) имеют одинаковые фазы; во всех других случаях j ¹ 0.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Зависимость j от w при разных коэффициентах d графически представлена на рис. 212, из которого следует, что при изменении w изменяется и сдвиг фаз j. Из формулы (147.9) вытекает, что при w =0 j =0, а при w = w 0 независимо от значения коэффициента затухания j = p /2, т. е. сила (напряжение) опережает по фазе колебания на p /2. При дальнейшем увеличении w сдвиг фаз возрастает и при w > > w 0 j ® p, т. е. фаза колебаний почти противоположна фазе внешней силы (переменного напряжения). Семейство кривых, изображенных на рис. 212, называется фазовыми резонансными кривыми.
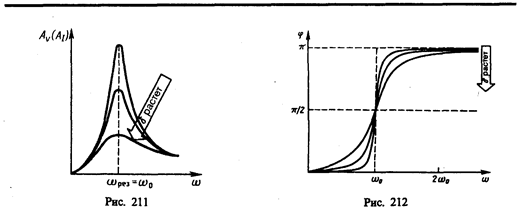
Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так, радиотехника, прикладная акустика, электротехника используют явление резонанса.
§ 148. Переменный ток
Установившиеся вынужденные электромагнитные колебания (см. § 147) можно рассматривать как протекание в цепи, содержащей резистор, катушку индуктивности и конденсатор, переменного тока. Переменный ток можно считать квазистационарным, т. е. для него мгновенные значения силы тока во всех сечениях цепи практически одинаковы, таккак их изменения происходят достаточно медленно, а электромагнитные возмущения распространяются по цепи со скоростью, равной скорости света. Для мгновенных значений квазистационарных токов выполняются закон Ома и вытекающие из него правила Кирхгофа, которые будут использованы применительно к переменным токам (эти законы уже использовались при рассмотрении электромагнитных колебаний).
Рассмотрим последовательно процессы, происходящие на участке цепи, содержащем резистор, катушку индуктивности и конденсатор, к концам которого приложено переменное напряжение
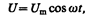 (149.1)
(149.1)
где U m — амплитуда напряжения.
1. Переменный ток, текущий через резистор сопротивлением R (L ®0, C ®0) (рис. 213, а). При выполнении условия квазистационарности ток через резистор определяется законом Ома:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
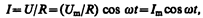
где амплитуда силы тока I m= U m /R.
Для наглядного изображения соотношений между переменными токами и напряжениями воспользуемся методом векторных диаграмм. На рис. 213, б дана векторная диаграмма амплитудных значений тока I m и напряжения U m на резисторе (сдвиг фаз между I m и U m равен нулю).

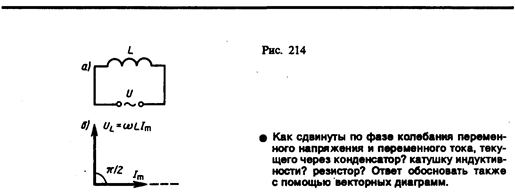
2. Переменный ток, текущий через катушку индуктивностью L (R ®0, C ®0) (рис. 214, а). Если в цепи приложено переменное напряжение (149.1), то в ней потечет переменный ток, в результате чего возникнет э.д.с. самоиндукции (см. (126.3)) 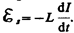 . Тогда закон Ома (см. (100.3)) для рассматриваемого участка цепи имеет вид
. Тогда закон Ома (см. (100.3)) для рассматриваемого участка цепи имеет вид
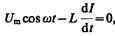
откуда
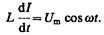 (149.2)
(149.2)
Таккак внешнее напряжение приложено к катушке индуктивности, то
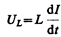 (149.3)
(149.3)
есть падение напряжения на катушке. Из уравнения (149.2) следует, что
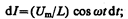
после интегрирования, учитывая, что постоянная интегрирования равна нулю (так как отсутствует постоянная составляющая тока), получим
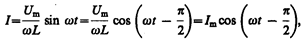 (149.4)
(149.4)
где I m= U m/(wL). Величина
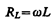 (149.5)
(149.5)
называется реактивным индуктивным сопротивлением (или индуктивным сопротивлением). Из выражения (149.5) вытекает, что для постоянного тока (w = 0) катушка индуктивности не имеет сопротивления. Подстановка значения U m =wLI m в выражение (149.2) с учетом (149.3) приводит к следующему значению падения напряжения на катушке индуктивности:
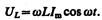 (149.6)
(149.6)
Сравнение выражений (149.4) и (149.6) приводит к выводу, что падение напряжения UL опережает по фазе ток I, текущий через катушку, на p /2, что и показано на векторной диаграмме (рис. 214, б).
3. Переменный ток, текущий через конденсатор емкостью С (R ®0, L ®0) (рис. 215, в). Если переменное напряжение (149.1) приложено к конденсатору, то он все время перезаряжается, и в цепи течет переменный ток. Так как все внешнее напряжение приложено к конденсатору, а сопротивлением подводящих проводов можно пренебречь, то

Сила тока
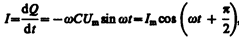 (149.7)
(149.7)
где
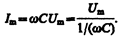
Величина

называется реактивным емкостным сопротивлением (или емкостным сопротивлением). Для постоянного тока (w = 0) RС = ¥, т. е. постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе
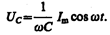 (149.8)
(149.8)
Сравнение выражений (149.7) и (149.8) приводит к выводу, что падение напряжения UС отстает по фазе от текущего через конденсатор тока I на p /2. Это показано на векторной диаграмме (рис. 215, б).
4. Цепь переменного тока, содержащая последовательно включенные резистор, катушку индуктивности и конденсатор. На рис. 216, а представлен участок цепи, содержащий резистор сопротивлением R, катушку индуктивностью L и конденсатор емкостью С, к концам которого приложено переменное напряжение (149.1). В цепи возникнет переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения UR, UL и UC. На рис. 216, б представлена векторная диаграмма амплитуд падений напряжений на резисторе (UR), катушке (UL) и конденсаторе (UC). Амплитуда U m приложенного напряжения должна быть равна векторной сумме амплитуд этих падений напряжений. Как видно из рис. 216, б, угол j определяет разность фаз между напряжением и силой тока. Из рисунка следует, что (см. также формулу (147.16))
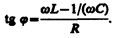 (149.9)
(149.9)
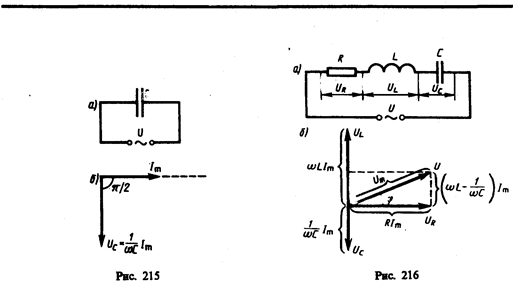
Из прямоугольного треугольника получаем  откуда амплитуда силы тока имеет значение
откуда амплитуда силы тока имеет значение
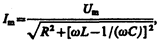 (149.10)
(149.10)
совпадающее с (147.15).
Следовательно, если напряжение в цепи изменяется по закону U = U m cos w t, то в цепи течет ток
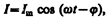 (149.11)
(149.11)
где j и I m определяются соответственно формулами (149.9) и (149.10). Величина
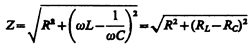 (149.12)
(149.12)
называется полным сопротивлением цепи, а величина
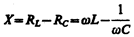
– реактивным сопротивлением.
Рассмотрим частный случай, когда в цепи отсутствует конденсатор. В данном случае падения напряжений UR и UL в сумме равны приложенному напряжению U. Векторная диаграмма для данного случая представлена на рис. 217, из которого следует, что
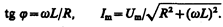 (149.13)
(149.13)

Выражения (149.9) и (149.10) совпадают с (149.13), если в них 1/(wC) = 0, т.е. С =¥. Следовательно, отсутствие конденсатора в цепи означает С =¥, а не С= 0. Данный вывод можно трактовать следующим образом: сближая обкладки конденсатора до их полного соприкосновения, получим цепь, в которой конденсатор отсутствует (расстояние между обкладками стремится к нулю, а емкость — к бесконечности; см. (94.3)).
§ 150. Резонанс напряжений
Если в цепи переменного тока, содержащей последовательно включенные конденсатор, катушку индуктивности и резистор (см. рис. 216),
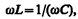 (150.1)
(150.1)
то угол сдвига фаз между током и напряжением (149.9) обращается в нуль (j =0), т. е. изменения тока и напряжения происходят синфазно. Условию (150.1) удовлетворяет частота
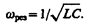 (150.2)
(150.2)
В данном случае полное сопротивление цепи Z (149.12) становится минимальным, равным активному сопротивлению R цепи, и ток в цепи определяется этим сопротивлением, принимая максимальные (возможные при данном U m) значения. При этом падение напряжения на активном сопротивлении равно внешнему напряжению, приложенному к цепи (UR = U), а падения напряжений на конденсаторе (UC) и катушке индуктивности (UL) одинаковы по амплитуде и противоположны по фазе. Это явление называется резонансом напряжений (последовательным резонансом), а частота (150.2) — резонансной частотой. Векторная диаграмма для резонанса напряжений приведена на рис. 218, а зависимость амплитуды силы тока от w уже была дана на рис. 211.
В случае резонанса напряжений
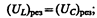
подставив в эту формулу значения резонансной частоты и амплитуды напряжений на катушке индуктивности и конденсаторе, получим
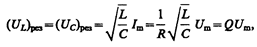
где Q — добротность контура, определяемая выражением (146.14). Так как добротность обычных колебательных контуров больше единицы, то напряжение как на катушке индуктивности, так и на конденсаторе превышает напряжение, приложенное к цепи. Поэтому явление резонанса напряжений используется в технике для усиления колебания напряжения какой-либо определенной частоты. Например, в случае резонанса на конденсаторе можно получить напряжение с амплитудой QU m (Q в данном случае—добротность контура, которая может быть значительно больше U m). Это усиление напряжения возможно только для узкого интервала частот вблизи резонансной частоты контура, что позволяет выделить из многих сигналов одно колебание определенной частоты, т. е. на радиоприемнике настроиться на нужную длину волны. Явление резонанса напряжений необходимо учитывать при расчете изоляции электрических линий, содержащих конденсаторы и катушки индуктивности, так как иначе может наблюдаться их пробой.
§ 151. Резонанс токов
Рассмотрим цепь переменного тока, содержащую параллельно включенные конденсатор емкостью С и катушку индуктивностью L (рис. 219). Для простоты допустим, что активное сопротивление обеих ветвей настолько мало, что им можно пренебречь. Если приложенное напряжение изменяется по закону U= U m сos w t (см. (149.1)), то, согласно формуле (149.11), в ветви 1С2 течет ток
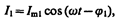
амплитуда которого определяется из выражения (149.10) при условии R= 0 и L =0:

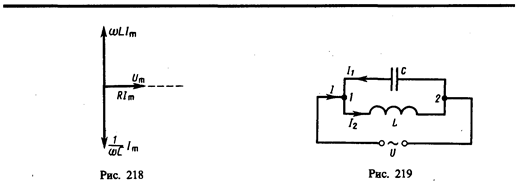
Начальная фаза j 1 этого тока по формуле (149.9) определяется равенством
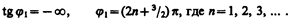 (151.1)
(151.1)
Аналогично, сила тока в ветви 1L2
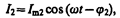
амплитуда которого определяется из (149.10) при условии R= 0 и С =¥ (условие отсутствия емкости в цепи, см. § 149):
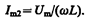
Начальная фаза j 2 этого тока (см. (149.9))
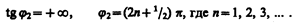 (151.2)
(151.2)
Из сравнения выражений (151.1) и (151.2) вытекает, что разность фаз токов в ветвях 1С2 н 1L2 равна j 1 —j 2 =p, т. е. токи в ветвях противоположны по фазе. Амплитуда силы тока во внешней (неразветвленной) цепи
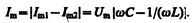
Если w = w рез = 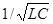 , то I m1= I m2и I m=0. Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты w приложенного напряжения к резонансной частоте w рез называется резонансом токов (параллельным резонансом). В данном случае для резонансной частоты получили такое же значение, как и при резонансе напряжений (см. § 150).
, то I m1= I m2и I m=0. Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты w приложенного напряжения к резонансной частоте w рез называется резонансом токов (параллельным резонансом). В данном случае для резонансной частоты получили такое же значение, как и при резонансе напряжений (см. § 150).
Амплитуда силы тока I m оказалась равна нулю потому, что активным сопротивлением контура пренебрегли. Если учесть сопротивление R, то разность фаз j 1 —j 2будет равна p, поэтому при резонансе токов амплитуда силы тока I m будет отлична от нуля, но примет наименьшее возможное значение. Таким образом, при резонансе токов во внешней цепи токи I 1 и I 2 компенсируются и сила тока I в подводящих проводах достигает минимального значения, обусловленного только током через резистор. При резонансе токов силы токов I 1 и I 2 могут значительно превышать силу тока I.
Рассмотренный контур оказывает большое сопротивление переменному току с частотой, близкой к резонансной. Поэтому это свойство резонанса токов используется в резонансных усилителях, позволяющих выделять одно определенное колебание из сигнала сложной формы. Кроме того, резонанс токов используется в индукционных печах, где нагревание металлов производится вихревыми токами (см. § 125). В них емкость конденсатора, включенного параллельно нагревательной катушке, подбирается так, чтобы при частоте генератора получился резонанс токов, в результате чего сила тока через нагревательную катушку будет гораздо больше, чем сила тока в подводящих проводах.
§ 152. Мощность, выделяемая в цепи переменного тока
Мгновенное значение мощности переменного тока равно произведению мгновенных значений напряжения и силы тока:
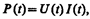
где U(t)=U mcos wt, I(t)=I mcos(wt – j) (см. выражения (149.1) и (149.11)). Раскрыв cos(wt – j), получим
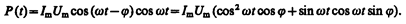

Практический интерес представляет не мгновенное значение мощности, а ее среднее значение за период колебания. Учитывая, что á cos2 w t ñ = 1/2, á sin w t cos w t ñ = 0, получим
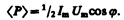 (152.1)
(152.1)
Из векторной диаграммы (см. рис. 216) следует, что U m сos j = RI m. Поэтому
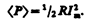
Такую же мощность развивает постоянный ток 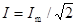 .
.
Величины
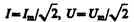
называются соответственно действующими (или эффективными) значениями тока и напряжения. Все амперметры и вольтметры градуируются по действующим значениям тока и напряжения.
Учитывая действующие значения тока и напряжения, выражение средней мощности (152.1) можно запасать в виде
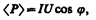 (152.2)
(152.2)
где множитель соs j называется коэффициентом мощности.
Формула (152.2) показывает, что мощность, выделяемая в цепи переменного тока, в общем случае зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи реактивное сопротивление отсутствует, то cos j =1 и P=IU. Если цепь содержит только реактивное сопротивление (R =0), то cos j =0 и средняя мощность равна нулю, какими бы большими ни были ток и напряжение. Если cos j имеет значения, существенно меньшие единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приведет либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить соs j, наименьшее допустимое значение которого для промышленных установок составляет примерно 0, 85.
Задачи
18.1. Материальная точка, совершающая гармонические колебания с частотой n = 2 Гц, в момент времени t= 0 проходит положение, определяемое координатой х 0 — 6 см, со скоростью v 0=14 см/с. Определить амплитуду колебания. [6, 1 см]
18.2. Полная энергия гармонически колеблющейся точки равна 30 мкДж, а максимальная сила, действующая на точку, равна 1, 5 мН. Написать уравнение движения этой точки, если период колебаний равен 2 с, а начальная фаза p/3. [x=0, 04cos(p t +p/3)]
18.1. При подвешивании грузов массами m 1 = 500 г и m 2 = 400 г к свободным пружинам последние удлинились одинаково (D l =15 см). Пренебрегая массой пружин, определить: 1) периоды колебаний грузов; 2) который из грузов при одинаковых амплитудах обладает большей энергией и во сколько раз. [1) 0, 78 с; 2) 1, 25]
18.4. Физический маятник представляет собой тонкий однородный стержень длиной 25 см. Определить, на каком расстоянии от центра масс должна быть точка подвеса, чтобы частота колебаний была максимальной. [7, 2 см]
18.5. Два математических маятника, длины которых отличаются на D l = 16 см, совершают за одно и то же время: один n 1=10 колебаний, другой n 2= 6 колебаний. Определить длины маятников l 1 и l 2. [ l 1=9 см, l 2=25 см]
18.6. Колебательный контур содержит катушку с общим числом витков, равным 50, индуктивностью 5 мкГн и конденсатор емкостью 2 нФ. Максимальное напряжение на обкладках конденсатора составляет 150 В. Определить максимальный магнитный поток, пронизывающий катушку. [0, 3 мкВб]
18.7. Разность фаз двух одинаково направленных гармонических колебаний одинакового периода, равного 8 с, и одинаковой амплитуды 2 см составляет p/4. Написать уравнение движения, получающегося в результате сложения этих колебаний, если начальная фаза одного из них равна нулю. [ х =0, 037 соs (p t/ 4+p/8)]
18.8. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями х= cosp t и y= cosp t/2. Определить уравнение траектории точки и вычертить ее с нанесением масштаба. [2 y 2– х =1]
18.9. За время, за которое система совершает 100 полных колебаний, амплитуда уменьшается в три раза. Определить добротность системы. [286]
18.10. Колебательный контур содержит катушку индуктивностью 25 мГн, конденсатор емкостью 10 мкФ и резистор сопротивлением 1 Ом. Заряд на обкладках конденсатора Q m=1 мКл. Определить: 1) период колебаний контура; 2) логарифмический декремент затухания колебаний; 3) уравнение зависимости изменения напряжения на обкладках конденсатора от времени. [1) 3, 14 мс; 2) 0, 06; 3) U= 100 e– 20 t cos636 pt ]
18.11. Последовательно соединенные резистор с сопротивлением 110 Ом и конденсатор подключены к внешнему переменному напряжению с амплитудным значением 110 В. Оказалось, что амплитудное значение установившегося тока в цепи 0, 5 А. Определить разность фаз между током и внешним напряжением. [60°]
18.12. В цепь переменного тока частотой 50 Гц включена катушка длиной 50 см и площадью поперечного сечения 10 см2, содержащая 3000 витков. Определить активное сопротивление катушки, если сдвиг фаз между напряжением и током составляет 60°. [4, 1 Ом]
18.13. Генератор, частота которого составляет 32 кГц и амплитудное значение напряжения равно 120 В, включен в резонирующую цепь, емкость которой 1 нФ. Определить амплитудное значение напряжения на конденсаторе, если активное сопротивление цепи 5 Ом. [119 кВ]
18.14. Колебательный контур содержит катушку индуктивностью 5 мГн и конденсатор емкостью 2 мкФ. Для поддержания в колебательном контуре незатухающих гармонических колебаний с амплитудным значением напряжения на конденсаторе 1 В необходимо подводить среднюю мощность 0, 1 мВт. Считая затухание колебаний в контуре достаточно малым, определить добротность данного контура. [100]
Глава 19Упругие волны
§ 153. Волновые процессы. Продольные и поперечные волны
Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начнет колебаться. Иначе говоря, фазы колебаний частиц среды и источника тем больше отличаются друг от друга, чем больше это расстояние. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т. е. непрерывно распределенная в пространстве и обладающая упругими свойствами.
Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны.
Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т. е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные.
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. На рис. 220 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси х, т. е. приведена зависимость между смещением x частиц среды, участвующих в волновом процессе, и расстоянием х этих частиц (например, частицы В) от источника колебаний О для какого-то фиксированного момента времени t. Приведенный график функции x (x, t)похож на график гармонического колебания, однако они различны по существу. График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени, а график колебаний — зависимость смещения данной частицы от времени.
|
|
