💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Прямая и обратная геодезические задачи.

Графический способ определения площади на картах и планах.

Существует три способа определения площади участков: геометрический, аналитический и механический. На местности применяют два первых способа, на картах и планах - все три способа.

Геометрический способ - это вычисление площади геометрических фигур по длинам сторон и углам между ними, значения которых можно получить только из измерений.

Таким образом, вариант с измерением трех сторон треугольника оказывается самым эффективным, так как в нем не требуется измерять углы.

Четырехугольник, как геометрическая фигура, может быть параллелограммом, ромбом, трапецией, прямоугольником, квадратом; но как участок местности его следует считать фигурой произвольной формы, так как обеспечение геометрических свойств той или иной фигуры на местности требует дополнительных измерений.

Применение геометрического способа на местности требует разбиения участка на простые геометрические фигуры, что возможно лишь при наличии видимости внутри участка.

При определении площади участков на топографических планах и картах стороны и высоты треугольников, стороны и диагонали четырехугольников нужно измерять с помощью поперечного масштаба.

Для определения площади на карте или плане геометрическим способом часто используют палетку - лист прозрачной бумаги, на котором нанесена сетка квадратов или параллельных линий. Палетку с квадратами накладывают на участок и подсчитывают, сколько квадратов содержится в данном участке; неполные квадраты считают отдельно, переводя затем их сумму в полные квадраты. Площадь участка вычисляют по формуле:

P=n*(a*M)2,

где a - длина стороны квадрата,

M - знаменатель масштаба карты,

n - количество квадратов на участке.

Смысл угловой и линейной невязок, как они рассчитываются в замкнутом

Теодолитном ходе.

Определяют абсолютную невязку fD хода fD = √ f 2 x + f 2 y и записывают в ведомость с погрешностью до сотых долей метра.

Вычисляют относительную линейную невязку fD/∑ D где ∑ D - сумма длин сторон хода, выражаемая простой дробью с единицей в числителе. Для ее нахождения сумму длин сторон хода делят на абсолютную линейную невязку.

Если относительная невязка меньше 1/2000, невязки fx и fy распределяют, вводя поправки в вычисленные значения координат. Поправки вычисляют по формулам: ∆ xi = fx; Di/∑ D; ∆ yi = fxDi/∑ D, где ∆ xi, ∆ yi - поправки в вычисленные значения координат, вводимые с обратным невязкам знаком.

Прямая и обратная геодезические задачи.

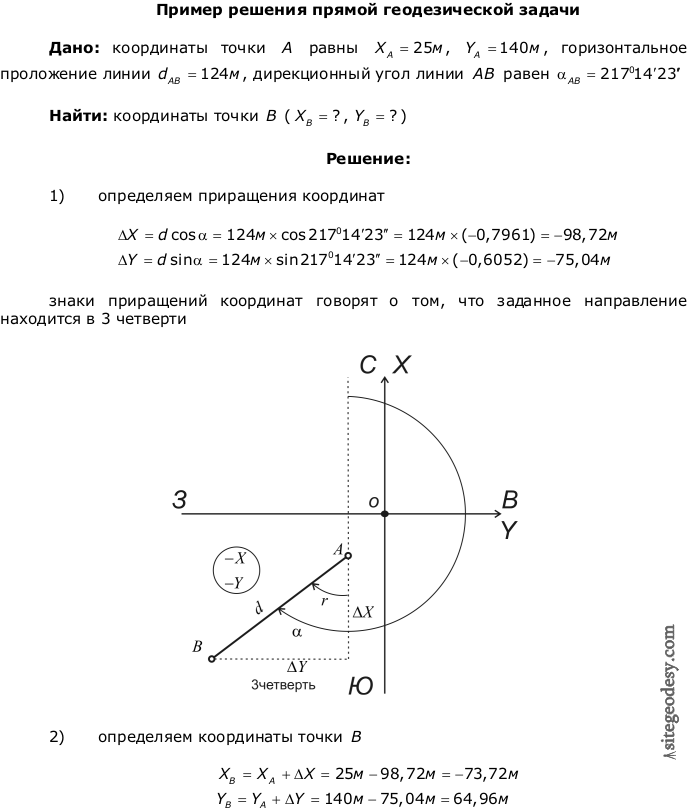
Прямая геодезическая задача заключается в том, что по известным координатам одной точки (например точка А), вычисляют координаты другой точки (например точка В), для чего необходимо знать горизонтальное проложение (длину) линии между этими точками () и дирекционный угол этой линии.

Решение прямой геодезической задачи выполняется по формулам:

где 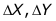называются приращениями координат и определяются из решения прямоугольного треугольника :

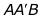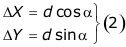
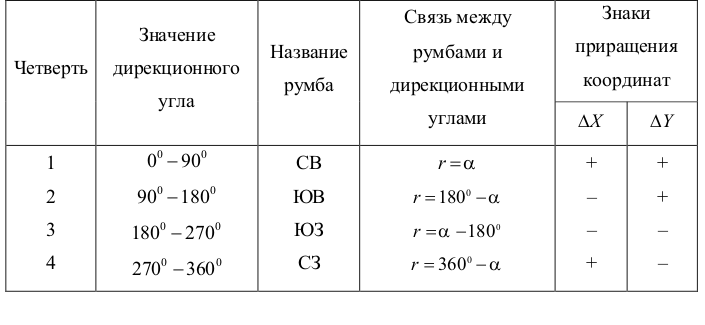
Знаки приращений координат (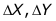) зависят от четверти, в которой находится заданное направление и определяются по формулам 2, с помощью рисунка приведенного выше, или с помощью таблицы

Обратная геодезическая задача заключается в том, что по известным координатам двух точек (например точек А и В) вычисляют горизонтальное проложение (длину) линии между этими точками () и дирекционный угол этой линии .

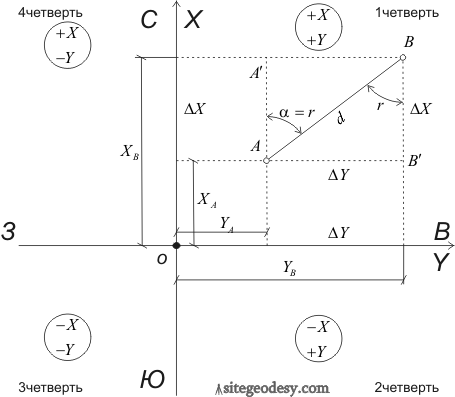
Решение обратной геодезической задачи выполняется в следующем порядке:

1) вычисляют приращения координат

2) из решения прямоугольного треугольника 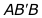определяют румб линии :

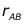откуда

3) по знакам приращений координат (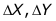) с помощью таблицы определяют в какой четверти находится заданное направление и по известному румбу линии (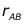) определяют дирекционный угол линии

4) определяют горизонтальное проложение (длину линии)

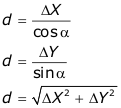
Горизонтальное проложение линии может быть вычислено трижды, что является хорошим контролем вычислений.