
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 4–6
|
|
8. Транспортная задача
Рассмотрим одну из важнейших задач линейного программирования - транспортную задачу. Это задача наиболее рационального прикрепления пунктов отправления грузов к пунктам их назначения, чтобы общая стоимость перевозок была минимальной. Являясь одной из задач линейного программирования, транспортная задача, конечно, может быть принципиально решена алгоритмом симплекс-метода.
Но непосредственное применение симплекс-метода к транспортной задаче обычно не целесообразно, так как, являясь универсальным методом решения любой задачи линейного программирования, он не учитывает специфики условий транспортной задачи, и применение симплекс-метода к ее решению оказывается слишком громоздким.
Один из наиболее распространенных методов решения транспортной задачи – метод потенциалов, полностью использующий особенности условий этой задачи и приводящий к цели значительно быстрее и проще, симплекс-метод.
Транспортная задача формулируется так:
В данных 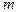 пунктах производится некоторый однородный продукт в количествах соответственно
пунктах производится некоторый однородный продукт в количествах соответственно 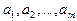 единиц. Этот продукт следует доставить в
единиц. Этот продукт следует доставить в 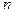 заданных пунктов назначения, потребляющих его соответственно в количествах
заданных пунктов назначения, потребляющих его соответственно в количествах 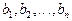 . Пусть стоимость перевозки единицы продукта из
. Пусть стоимость перевозки единицы продукта из 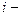 го пункта производства в
го пункта производства в 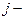 й пункт назначения (потребления) равна
й пункт назначения (потребления) равна 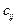 , а соответствующее количество единиц перевозимого продукта равно
, а соответствующее количество единиц перевозимого продукта равно 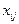 (
(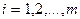 ;
;  ) Условия задачи запишем компактно в виде следующей таблицы (двойной матрицы):
) Условия задачи запишем компактно в виде следующей таблицы (двойной матрицы):
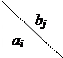
| b 1 | b 2 | … | … | bn |
| a 1 | c 11 x 11 | c 12 x 12 | … | … | c 1 n x 1 n |
| a 2 | c 21 x 21 | c 22 x 22 | … | … | c 2 n x 2 n |
| … | … | … | … | … | … |
| … | … | … | … | … | … |
| am | cm 1 xm 1 | cm 2 xm 2 | … | … | cmn xmn |
|
Совокупность 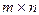 чисел
чисел 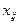 , т.е. матрицу
, т.е. матрицу 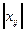 , будем называть планом перевозок, а матрицу
, будем называть планом перевозок, а матрицу 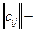 матрицей транспортных издержек.
матрицей транспортных издержек.
План называется допустимым, если числа 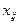 удовлетворяют следующим естественным ограничениям:
удовлетворяют следующим естественным ограничениям:
|
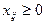 (
( ;
;  ),
),
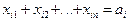 (
( ),
),
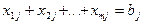 (
( ),
),
в которых первые 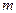 равенств означают, что из каждого пункта производства вывозится весь продукт, а последние
равенств означают, что из каждого пункта производства вывозится весь продукт, а последние 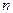 равенств означают, что каждый пункт потребления полностью удовлетворяется.
равенств означают, что каждый пункт потребления полностью удовлетворяется.
Транспортная задача заключается в отыскании среди допустимых планов оптимального, т.е. такого, по которому общая стоимость перевозок
|

минимальна.
Если система (1.4.2) совместна,
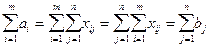 ,
,
таким образом, условие
|
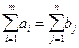
необходимо для совместности (1.4.2). Условие (1.4.4) является и достаточным для совместности (1.4.2). В самом деле, при выполнении условия (1.4.4) значения
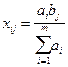 (
( ;
;  ),
),
как легко проверить, удовлетворяют системе (1.4.2) (нетрудно проверить, что любое из 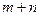 уравнений (1.4.2) является следствием остальных
уравнений (1.4.2) является следствием остальных 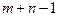 , образующих линейно независимую систему).
, образующих линейно независимую систему).
Таким образом, транспортная задача относится к задачам линейного программирования и решается алгоритмом симплекс-метода. Однако ввиду исключительной практической важности и специфики ограничений (1.4.2):
а) ограничения заданы в виде уравнений,
б) каждая неизвестная входит лишь в два уравнения,
в) коэффициенты при неизвестных – единицы, для ее решения созданы специальные алгоритмы, значительно менее громоздкие, чем алгоритм симплекс-метода. Один из них – м е т о д п о т е н ц и а л о в – представляет собой приспособление общего метода Л, В, Канторовича для решения транспортной задачи.
Другой, так называемый в е н г е р с к и й м е т о д усовершенствован для решения частного случая транспортной задачи – задачи о назначениях (или о выборе).
|
|