
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Игры с ненулевой суммой и кооперативные игры
|
|
В игре с ненулевой суммой уже становится необязательно, чтобы один из участников выигрывал, а другой проигрывал; напротив, они могут и выигрывать, и проигрывать одновременно. Поскольку интересы игроков теперь не являются полностью противоположными, их поведение становится более разнообразным. Так, например, если в игре с нулевой суммой каждому игроку невыгодно было сообщать другому свою стратегию (это могло уменьшить его выигрыш), то в игре с ненулевой суммой становится желательным как-то координировать свои действия с партнером или каким-либо способом влиять на его действия.
Игры с ненулевой суммой могут быть кооперативными и некооперативными. В некооперативных играх игроки принимают решения независимо друг от друга либо потому, что осуществление соглашения невозможно, либо потому, что оно запрещено правилами игры.
Один из подходов к решению некооперативных игр состоит в определении точек равновесия игры. Понятие равновесия в теории игр шире понятия оптимальности в теории оптимизации и включает последнее в качестве частного случая. В общем случае пара стратегий X, Y для Игрока 1 и Игрока 2 называется точкой равновесия по Нэшу, если ни одному из игроков невыгодно отклоняться от своей стратегии в одиночку, если выигрыш при этом не увеличивается.
Рассмотрим пример, когда матрица выигрышей игры имеет следующий вид:
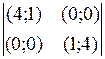
Легко видеть, что в данной игре пары стратегий х = (1, 0), у = (1, 0) и х = (0, 1), у = (0, 1) являются равновесными, т.е. Игроку 2 (1) не выгодно отклоняться от 1-й (2-й) стратегии, если Игрок 1 (2) придерживается 1-й (2-й) стратегии. Отметим также, что выигрыши в равновесных точках различны.
Доказано, что для любой конечной некооперативной игры с ненулевой суммой (называемой также биматричной игрой) всегда существует, по крайней мере, одна равновесная пара смешанных стратегий. В общем случае равновесное решение может быть неединственным, и каждому из них могут соответствовать различные значения выигрыша каждого из игроков.
Кооперативной игрой называется игра с ненулевой суммой, в которой игрокам разрешается обсуждать перед игрой свои стратегии и договариваться о совместных действиях, т.е. игроки могут образовывать коалиции. Основная задача в кооперативной игре состоит в дележе общего выигрыша между членами коалиции.
В случае игры двух лиц предполагается, что два игрока не могут воздействовать друг на друга, пока не придут к некоторому соглашению.
На множестве возможных выигрышей выделяется множество Парето-оптимальных решений, т.е. множество точек, принадлежащих некоторому множеству S, для которых увеличение выигрыша одного из игроков возможно только за счет уменьшения выигрыша его партнера.
Рассмотрим пример, в котором имеются два продавца, продающие определенный товар на рынке. Оба из них знают, что чем выше цена, тем меньше общий объем продаж. Для простоты предположим, что каждый из них может продать либо 400 единиц некоторого товара, либо 100 единиц. Известно, что при продаже 800 единиц на рынке складывается цена равная 100 фунтам, при 500 единицах — 200 фунтов, а при объеме продаж 200 единиц — 500 фунтов. Матрица выигрышей продавцов показана в нижеследующей таблице 7.5.
Таблица 7.5 – Матрица игры
| Продавец 1 / Продавец 2 | ||
| 40000/40000 | 80000/20000 | |
| 20000/80000 | 50000/50000 |
Если бы игроки имели возможность и желание согласовывать свои действия, то они решили бы продать по 100 единиц и получить прибыль по 50 000 каждый.
Предположим теперь, что по каким-либо причинам они принимают решения независимо друг от друга. Каковы оптимальные стратегии для игроков в этом случае? Пара стратегий (400, 100) не является ситуацией равновесия, так как в этом случае второму игроку выгодно изменить свою стратегию на 400 и тем самым увеличить свой выигрыш с 20000 до 40 000.
Если рассмотреть пару стратегий (100, 100), то она также не является ситуацией равновесия, поскольку каждому отдельному игроку выгодно поменять свою стратегию на 100 и получить вместо 50 000 выигрыш в 80 000. Если же мы рассмотрим пару стратегий (400, 400), то отклонение каждого отдельного игрока является для него невыгодным. Такую ситуацию мы называем ситуацией некооперативного равновесия.
Таким образом, основным определяющим свойством ситуации некооперативного равновесия является невыгодность для каждого отдельного игрока отклоняться от своей стратегии, входящей в ситуацию равновесия. В этом случае речь не идет о каких-либо договоренностях между игроками и поэтому такое равновесие называется некооперативным. Напротив, когда возможность достигать определенные договоренности между игроками существует, игроки стараются найти такую пару стратегий, для которой не существует другой пары, одновременно улучшающей вшпрыши обоих игроков. Такая пара стратегий называется ситуацией кооперативного равновесия. Таковыми являются пары стратегий (100, 100).
Этот пример игр можно отнести к так называемым биматричным играм, суть которых состоит в следующем. Пусть первый игрокимеет m чистых стратегий, а второй игрок имеет п чистых стратегий. Выигрыши первого игрока при различных выборах стратегий игроками задаются матрицей А 1=½ 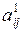 ½ — платежная матрица первого игрока, а второго игрока матрицей А 2=½
½ — платежная матрица первого игрока, а второго игрока матрицей А 2=½ 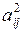 ½ — платежная матрица второго игрока. На практике решение в чистых стратегиях для биматричных игр встречается крайне редко, поэтому решение ищется в смешанных стратегиях, которые определяются так же как и для матричных игр соотношениями (7.3) и (7.4). Среднеожидаемые выигрыши игроков в этом случае определяются соотношениями
½ — платежная матрица второго игрока. На практике решение в чистых стратегиях для биматричных игр встречается крайне редко, поэтому решение ищется в смешанных стратегиях, которые определяются так же как и для матричных игр соотношениями (7.3) и (7.4). Среднеожидаемые выигрыши игроков в этом случае определяются соотношениями
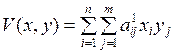 и
и 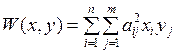 (7.5)
(7.5)
В биматричных играх существует несколько критериев оптимальности. Важнейшими из них являются критерий оптимальности по Парето и критерий, выделяющий ситуации равновесия по Нэшу. Основные определения этих двух подходов.
1. Оптимальность по Парето. Пусть имеется несколько целевых функций F1(z),..., Fn(z), каждую из которых хотят максимизировать. Вектор решения z называется оптимальным по Парето (или эффективным), если не существует другого вектора z*, для которого значения всех функций Fi(z) ≥ Fi (z*) и хотя бы одно неравенство строгое.
Суть данного подхода состоит в том, что рассматриваются решения, которые лучше по одному критерию, но хуже по другому, и нет такого вектора, который был бы лучше сразу по всем критериям.
Множество эффективных векторов называется множеством Парето, а любой вектор этого множества — оптимумом по Парето.
В случае биматричной игры z = (x, у), а в качестве целевых функций рассматриваются функции V (x, y)и W (х, у), заданные соотношениями (5.5).
2. Ситуации равновесия по Нэшу. Это такая пара смешанных стратегий (х*, у*), что для любых произвольных стратегий х и у выполняются
неравенства V (x*, у*) ≥ V (х, у* )и W (x*, у*) ≥ W (x*, у).
Смысл ситуации равновесия в том, что никому из игроков в одиночку не выгодно от нее отклоняться, его выигрыш при этом не увеличивается.
Справедлива следующая основная теорема теории биматричных игр.
Теорема Нэша. Существует хотя бы одна ситуация равновесия в любой биматричной игре.
Замечание. В разных ситуациях равновесия (их может быть несколько) выигрыши игроков различны.
7.5. Элементы теории игр п лиц
Во многих реальных ситуациях в процессе принятия решений участвует более двух игроков. Рассмотрим случай, когда участников игры трое или более. Пусть N= {1, 2,..., п }— множество игроков, х i — стратегия i -го игрока, Xi — множество стратегий i -го игрока; fi (x 1, …, x n) — функция выигрыша i -го игрока в зависимости от выбранных стратегий x 1, …, x n (ситуация игры). Такую игру называют игрой п лиц. Введем определения характеристической функции.
Определение. Функцию v (S) называют характеристической функцией для игры п лиц, если для любого подмножества S множества игроков N (S Î N) v (S) — максимальный суммарный гарантированный выигрыш игроков подмножества S при условии их оптимальных совместных действий. Или в математическом виде
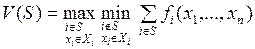 (7.6.)
(7.6.)
Оптимальная стратегия для коалиции гарантирует с одной стороны, что сумма индивидуальных выигрышей не будет меньше того, что может себе обеспечить коалиция в целом, а с другой стороны, что выигрыш каждого игрока не должен быть меньше того количества, которое он может себе обеспечить самостоятельно.
|
|