
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример решения экономической задачи методами теории игр
|
|
Предположим, необходимо определить наиболее оптимальный вариант организации страховой защиты инвестиционного проекта. Инвестором проведен конкурс по выбору наиболее надежной страховой организации. Однако, более полной защитой для крупного проекта будет являться страховка не одной компанией-победителем, а двумя компаниями – лидерами рейтинга конкурса (сострахование или страховой пул). Но стоимость страхования (страховой тариф), предлагаемый пулом, выше, чем у компании-победителя конкурса.
Трудно определить целесообразность для инвестора заключения договора страхования с пулом по более высоким тарифам, чем предложенные в заявке организации-победителя. Важным моментом при принятии такого решения является возможность ошибки при определении компании-победителя. Данная процедура выбора страховой компании, как и любая другая, может содержать ошибочные данные и привести к неправильным выводам. Вероятность наступления такого события (возникновения ошибки) не определена, что приводит к возникновению рисковой для инвестора ситуации. Традиционно методом решения таких задач являются игры с природой теории матричных игр.
Формально решение задач методом матричных игр с природой должно начинаться с определения вариантов решения, условий, требующих рассмотрения, и построения платежной матрицы, или матрицы игры.
В нашем случае варианты решения таковы:
А1 – заключение договора страхования с компанией-победителем конкурсного отбора, по предлагаемым ею тарифам;
А2 – заключение договора страхования со страховым пулам по завышенным тарифам;
А3 – отказ от заключения договора страхования.
Условия, требующие рассмотрения, следующие:
Р1 – решения о надежности победителя конкурса принято верно, то есть методика не содержит ошибку;
Р2 – решение о победителе неверно, неверна последовательность ранжирования компаний, но в целом компании, набравшие большее количество баллов, надежны;
Р3 – решение о победителе неверно, методика содержит ошибку, все компании ненадежны.
Для построения платежной матрицы необходимо выбрать критерий определения правильности решений. В качестве критерия выберем эффективность страхования. Под эффективностью страхования будем понимать разницу между страховой суммой (суммой, на которую застрахован объект) и страховым взносом (платой за страхование). Проведем анализ принятия решения на примере страхования строительства 1 километра автодороги второй категории по полному пакету рисков. Примем нормативную стоимость строительства такой автомобильной дороги 17000 тыс. руб.
Страховой тариф при страховании по схеме А1 равен 2, 05. Тогда страховой взнос составит 17000*2, 05%=348, 5 тыс. рублей, а искомый показатель – эффективность страхования – составит 17000-348, 5=16651, 5 тыс. руб. это значение верно при условии правильности выбора победителя – условии Р1. При условии Р2 и Р3 появляется возможность банкротства компании и, как следствие, невыплата страхователю страхового возмещения. Вероятность банкротства равна 0, 5, тогда эффективность страхования составит 8325, 75 тыс. руб.
Страховой тариф при принятии решения А2 составит 2, 12%. Определим страховой взнос: 17000*2, 12%=360, 4 тыс. руб. Тогда эффект страхования при условии Р1 равен 17000-360, 4=16639, 6 тыс.руб. При условии Р3 (ошибка определения финансовой устойчивости компаний) риск банкротства членов страхового пула имеет вероятность 0, 5, следовательно, эффективность страхования становится равной 8319, 8 тыс. руб. однако, если ошибка произошла лишь при распределении верхних строк рейтинга оферт, вероятность получения страхователем возмещения возрастает до 0, 75, тогда эффект составит 12479, 7 тыс.руб.
Если страховщик не заключает договор страхования вообще, то при условии Р1 он не получает ни эффекта, ни затрат. Однако, при условии Р2 выигрыш страхователя составит 348, 5 тыс. рублей (то есть величину уплаченного страхового взноса), а при условии Р3 – соответственно, 360, 4 тыс.руб.
Платежная матрица выглядит следующим образом (таблица 7.6).
Таблица 7.6 - Матрица игры
| Р1 | Р2 | Р3 | |
| А1 | 16651, 5 | 8325, 75 | 8325, 75 |
| А2 | 16639, 6 | 12479, 7 | 8319, 8 |
| А3 | 348, 5 | 360, 4 |
Рассмотрим варианты решения задачи с использованием классических критериев.
1. Критерий минимакса (максиминный критерий Вальда). Это позиция крайнего пессимизма, рассчитанная на худший случай. Для совершения выбора матрица решений дополняется еще одним столбцом из наименьших результатов построчно. Необходимо выбрать максимальное значение этого столбца. Таким образом, выбранные решения полностью исключают риск. Решения с использованием данного критерия применяются, когда возможность проявления внешних состояний Р неизвестна.
Решение задачи данным методом показано в таблице 7.7.
Таблица 7.7 - Решение игры по критерию минимакса
| Р1 | Р2 | Р3 | Min aij | |
| А1 | 16651, 5 | 8325, 75 | 8325, 75 | 8325, 75 |
| А2 | 16639, 6 | 12479, 7 | 8319, 8 | 8319, 8 |
| А3 | 348, 5 | 360, 4 |
Максимальный элемент добавленного столбца – 8325, 75 – принадлежит строке А1. То есть по критерию минимакса оптимальной является первая стратегия – заключить договор страхования с компанией «Энергогарант». Такое решение позволит при неопределенной вероятности ошибки определения победителя получить максимальный эффект.
2. Критерий Сэвиджа (критерий наименьшего сожаления). Применяется при неизвестной вероятности проявления состояний природы. Игрок руководствуется не матрицей выигрышей, а матрицей рисков. На первом этапе вычисляются величины:
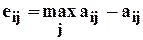 , (7.12)
, (7.12)
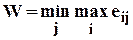 , (7.13)
, (7.13)
где аij – элементы платежной матрицы;
eij – риски; W – решение задачи.
Правило выбора соответственно критерию Сэвиджа трактуется следующим образом:
- каждый элемент матрицы решений 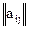 вычитается из наибольшего результата max аij соответствующего столбца,
вычитается из наибольшего результата max аij соответствующего столбца,
- разности еij образуют матрицу остатков. Эта матрица пополняется столбцом наибольших разностей. Выбирают вариант, в строках которого стоят минимальный элемент данного столбца.
Согласно критерию Сэвиджа, построим матрицу рисков и найдем оптимальное решение.
Таблица 7.8 - Решение игры по критерию Сэвиджа
| Р1 | Р2 | Р3 | Мах еij | |
| А1 | 4153, 95 | 4153, 95 | ||
| А2 | 11, 9 | 5, 95 | 11, 9 | |
| А3 | 16651, 5 | 12131, 2 | 7965, 35 | 16651, 5 |
Минимальная сумма остатков (рисков) равна 11, 9 и является элементом строки А2, что свидетельствует о целесообразности выбора второй стратегии.
3. Критерий Байеса-Лапласа. Данный критерий используется, когда вероятности появления условий Р известны и не зависят от времени. В нашем случае решение, принятое с применением данного критерия, является более приемлемым, чем предыдущие.
Так как применяемая методика оценки конкурсных заявок основана на богатом теоретическом и практическом материале и использует не только субъективные оценки, но и математический инструментарий, возможно предположение о распределении вероятности появления ошибки. Положим, вероятность абсолютно правильного выбора, то есть условия Р1, равна q1 и равна 0, 4. Вероятность условия Р2 равна q2 и равна 0, 5. Вероятность события Р3 равна q3 и равна 0, 1.
Соответствующее правило выбора можно выразить следующим образом: матрица решений 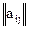 дополняется столбцом, содержащим математическое ожидание значений каждой из строк. Выбираются варианты, в строках которых стоит наибольшее значение математического ожидания.
дополняется столбцом, содержащим математическое ожидание значений каждой из строк. Выбираются варианты, в строках которых стоит наибольшее значение математического ожидания.
Таблица 7.9 - Решение игры по критерию Байеса-Лапласа
| Р1 | Р2 | Р3 | mi | |
| А1 | 16651, 5 | 8325, 75 | 8325, 75 | 11656, 05 |
| А2 | 16639, 6 | 12479, 7 | 8319, 8 | 13727, 67 |
| А3 | 348, 5 | 360, 4 | 210, 29 |
Как видим, максимум математического ожидания выигрыша равен 13727, 67 и находится в строке А2. Таки образом, при соответствующей вероятности ошибки в выборе победителя оптимальной для страхователя является стратегия заключения договора с участниками страхового пула, даже при завышении пулом страховых тарифов.
4. Критерий Ходжа-Лемана. Данный критерий опирается на критерии минимакса и Байеса-Лапласа. С помощью параметра v выражается степень доверия к используемому распределению вероятностей. Если доверие велико, то доминирует критерий Байеса-Лапласа, иначе - минимаксный критерий.
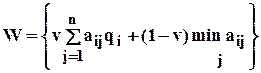 , (7.14)
, (7.14)
где 0≤ v≤ 1.
Правило выбора согласно критерию Ходжа-Лемана формулируется так: матрица решений  дополняется столбцом, составленным из средневзвешенных (с весом v=const) математических ожиданий и наименьшего результата каждой строки (соответственно формуле(7.14)). Отбираются варианты решений с максимальным значением элемента этого столбца.
дополняется столбцом, составленным из средневзвешенных (с весом v=const) математических ожиданий и наименьшего результата каждой строки (соответственно формуле(7.14)). Отбираются варианты решений с максимальным значением элемента этого столбца.
В нашем случае для решения задачи выбора варианта наиболее целесообразным является использование критерия Ходжа-Лемана, так как предположение о вероятности ошибки определения победителя возможно сделать лишь с определенной степенью доверия. Примем v=0, 95. Решение задачи представлено в таблице.
Таблица 7.10 - Решение игры по критерию Ходжа-Лемана
| Р1 | Р2 | Р3 | mi | V*mi | (1-v)* min aij | W | |
| А1 | 16651, 5 | 8325, 75 | 8325, 75 | 11656, 05 | 11073, 3 | 416, 3 | 11489, 6 |
| А2 | 16639, 6 | 12479, 7 | 8319, 8 | 13727, 7 | 13041, 3 | 415, 99 | 13457, 3 |
| А3 | 348, 5 | 360, 4 | 210, 29 | 199, 8 | 199, 8 |
По критерию Ходжа-Лемана наиболее выгодная для страхователя альтернатива – заключение договора страхования с участниками страхового пула.
Небольшое превышение страхового тарифа пула по сравнению с тарифами компании-победителя конкурса не несут больших финансовых убытков инвестору.
|
|