ВПЦ “Київський університет”, 2006 3 страница

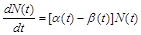, (1.2.14)

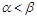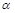яке доволі схоже з рівнянням радіоактивного розщеплення і збігається з ним при (якщо і 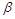– сталі). Це не дивно, оскільки при виведенні цих рівнянь використовувались однакові міркування. Інтегрування рівняння (1.2.14) дає:

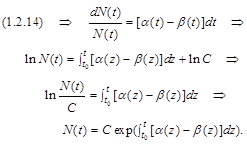
Довільна стала 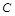знаходиться з початкової умови 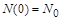, де 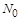– початкова чисельність населення, звідки 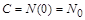, і розв’язок рівняння (1.2.14) остаточно буде таким:

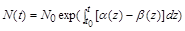. (1.2.15)

Проаналізуємо (1.2.15). При 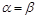чисельність населення залишається сталою. У цьому випадку розв’язком рівняння (1.2.14) буде стала величина 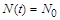(рис. 1.2.5).

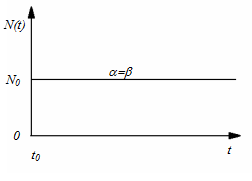
Рис. 1.2.5

Рівновага між народжуваністю і смертністю нестійка у тому розумінні, що навіть невелике порушення рівності 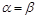приводить із часом до все більшого відхилення функції 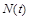від рівноважного значення 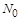. При сталих 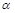і 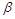за умови 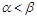чисельність населення зменшується і прямує до нуля при 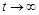за експоненціальним законом

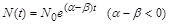
(рис. 1.2.6), а при 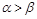зростає , знов-таки за експоненціальним законом (рис. 1.2.7), прямуючи до нескінченності при 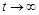. Такий результат став основою для побоювань Мальтуса про перенаселення Землі з усіма наслідками, які з цього випливають.

Як у даному прикладі, так і в багатьох розглянутих нами випадках можна вказати чимало очевидних обмежень застосування побудованої моделі. Звичайно, дуже складний процес зміни чисельності населення, який залежить до того ж від свідомого втручання самих людей, не може описуватися якимись простими закономірностями. Навіть в ідеальному випадку ізольованої біологічної популяції запропонована модель не відповідає реальності повною мірою хоча б через обмеженість ресурсів, які необхідні для її існування.

Однак це зауваження ніскільки не применшує ролі аналогій у побудові математичних моделей дуже складних явищ. Застосування аналогій базується на одній з найважливіших властивостей моделей – їх універсальності, тобто їх застосовності до об’єктів принципово різної природи. Так, припущення типу “швидкість зміни величини пропорційна значенню самої величини (або деякої функції від неї)” широко використовується в далеких одна від одної сферах знань.

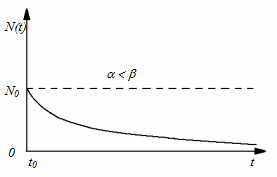
Рис. 1.2.6

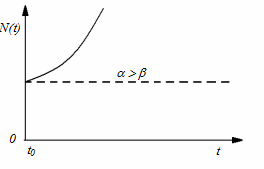
Рис. 1.2.7

2.2.4. Застосування ієрархічного підходу до створення моделей

Лише в окремих випадках буває зручною й виправданою побудова математичних моделей, навіть відносно простих об’єктів, одразу у всій повноті, з урахуванням усіх факторів, які є суттєвими для поведінки об’єктів. Тому природним є підхід, який реалізує принцип від простого – до складного, коли наступний крок робиться після досить детального вивчення не дуже складної моделі. При цьому виникає ланцюг (ієрархія) усе більш повних моделей, кожна з яких узагальнює попередні, включаючи їх як частинні випадки.

Побудуємо такий ієрархічний ланцюг на прикладі моделі багатоступеневої ракети. Нами вже було встановлено наприкінці підрозділу 2.2.1, що реальна одноступеневаракета неспроможна розвинути першу космічну швидкість. Причина цього – витрата пального на розгін непотрібної, відпрацьованої частини структурної маси. Тому під час руху ракети необхідно періодично позбуватися баласту. На практиці це означає, що ракета має складатися з кількох ступенів, які відкидаються після їх використання.

Нехай 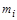– загальна маса і- го ступеня ракети; 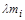– відповідна структурна маса (при цьому маса пального дорівнює величині 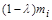); 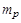– маса корисного вантажу. Припускається, що величини 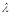і швидкість витікання газу 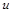однакові для всіх ступенів. Візьмемо для визначеності кількість ступенів 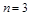. Початкова маса такої ракети буде рівною

.

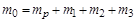Розглянемо момент, коли витрачено все паливо першого ступеня й маса ракети дорівнює величині

.

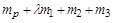Тоді за формулою Ціолковського (1.2.10)

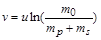
швидкість ракети у випадку, що розглядається, буде

.

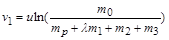Після досягнення цієї швидкості 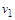структурна маса 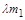відкидається і вмикається другий ступінь ракети. Маса ракети у цей момент становить

.

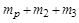Починаючи з цього моменту і до моменту повного вигоряння палива другого ступеня, ніщо не заважає скористатися вже збудованою моделлю, застосувавши її до випадку, що розглядається. Усі міркування стосовно збереження сумарного імпульсу й відповідні перетворення залишаються чинними (слід тільки врахувати, що ракета вже має початкову швидкість 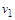). Тоді за формулою (1.2.10) після вигоряння палива у другому ступені ракета досягне швидкості

.

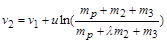Такі ж самі міркування є застосовними й до третього ступеня ракети. Після відключення її двигунів швидкість ракети дорівнюватиме

.

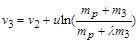Цей ланцюг неважко продовжити для будь-якого числа ступенів і отримати відповідні формули. У випадку ж 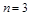для остаточної швидкості будемо мати

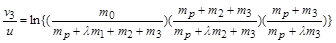
або, вводячи величини

,

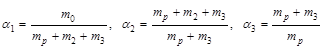отримаємо

.

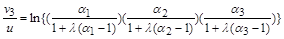Даний вираз є симетричним відносно до величин 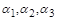, і неважко показати, що його максимум досягається в симетричному випадку, тобто коли 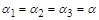. При цьому і= 3,

.

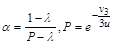Добуток 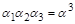дорівнює, як легко перевірити, відношенню 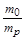, або

.

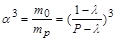Для багатоступеневої ракети, аналогічно, маємо

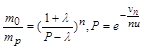, (1.2.16)

де 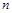– кількість ступенів ракети.

Проаналізуємо формулу (1.2.16). Приймемо 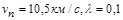. Тоді для 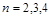отримаємо

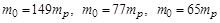
відповідно. Це означає, що двоступенева ракета придатна для виведення на орбіту деякої корисної маси (однак при одній тоні корисного вантажу необхідно мати ракету вагою 149 тон). Перехід до третього ступеня зменшує масу ракети майже у два рази (звичайно при цьому ускладнює її конструкцію), а чотирьохступенева ракета не дає помітного виграшу порівняно з триступеневою.

Побудова ієрархічного ланцюга дозволила відносно просто прийти до цих важливих висновків. Ієрархія математичних моделей часто будується й за протилежним принципом – від складного – до простого. У цьому випадку реалізується шлях згори – униз: – із досить загальної та складної моделі за відповідних спрощувальних припущень отримується послідовність усе простіших (але таких, які мають меншу сферу застосування) моделей.

2.2.5. Про нелінійність математичних моделей

Простота розглянутих математичних моделей значною мірою пов’язана з їх лінійністю. У математичному сенсі це важливе поняття означає, що є справедливим принцип суперпозиції, тобто будь-яка лінійна комбінація розв’язків (напр., їх сума) теж є розв’язком задачі. Користуючись принципом суперпозиції, не важко, знайшовши розв’язок у якомусь частинному випадку, побудувати розв’язок у більш складній ситуації. Тому про якісні властивості загального випадку можна міркувати за властивостями частинного – різниця між двома розв’язками має лише кількісний характер. Наприклад, збільшення у два рази швидкості витікання ракетного палива веде також до дворазового збільшення швидкості ракети, зменшення кута падіння світлового променя на дзеркальну поверхню означає таку саму зміну кута відбивання і т. д. Іншими словами, у випадку лінійних моделей відгук об’єкта на зміну якихось умов є пропорційним величині цієї зміни.

Для нелінійних явищ, математичні моделі яких не задовольняють принцип суперпозиції, знання про поведінку частини об’єкта ще не гарантує знання поведінки всього об’єкта, а його відгук на зміну умов може якісно залежати від величини цієї зміни.

Більшість реальних процесів і математичних моделей, які їм відповідають, є нелінійними.Лінійні ж моделі відповідають вельми частинним випадкам і, як правило, є лише першим наближенням до реальності. Наприклад, популяційні моделі відразу стають нелінійними, якщо прийняти до уваги обмеженість доступних для популяції ресурсів.

2.2.6. Висновки. Схема математичного моделювання

Процес побудови математичних моделей може бути умовно розбитий на такі етапи.

1. Побудова моделі починається зі словесно-змістового описання об’єкта чи явища. Окрім знань загального характеру про природу об’єкта і мету його дослідження, ця стадія може містити також деякі припущення(невагомий стрижень, товстий шар речовини, прямолінійне поширення світла тощо). Даний етап можна назвати формулюванням передмоделі.

2. Наступний етап – завершення ідеалізації об’єкта. Відкидаються всі фактори та ефекти, які вважаються не самими суттєвими для його поведінки. Наприклад, при складанні балансу матерії не враховувався, через його мализну, дефект мас, яким супроводжується радіоактивне розщеплення. За можливості припущення, які використовуються при ідеалізації, записуються в математичній формі. Наприклад, 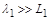– довжина вільного пробігу продуктів розщеплення 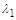значно більша за характерний розмір самого матеріалу 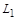(у прикладі про зберігання радіоактивних матеріалів). Це необхідно, щоб справедливість цих припущень піддавалась кількісному контролю.

3. Після виконання перших двох етапів можна переходити до вибору чи формулювання закону (варіаційного принципу, аналогії тощо), якому підлягає об’єкт, і його запису в математичній формі. За необхідності використовуються додаткові дані про об’єкт, які також записуються математично (напр., сталість величини 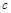для всіх траєкторій руху автомобіля – у прикладі про рух автомобіля з точки А у точку В з дотиком до деякої прямої). Слід мати на увазі, що навіть для простих об’єктів вибір відповідного закону є зовсім не тривіальною задачею.

4. Формулювання моделі завершує її “оснащення”. Наприклад, необхідно задати дані про початковий стан об’єкта (швидкість ракети та її масу в момент 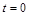) або інші його характеристики, без знання яких неможливо визначити поведінку об’єкта. І, нарешті, формулюється мета дослідження моделі (напр., досягнути розуміння закономірностей зміни популяції, встановити вимоги до конструкції ракети, яка запускає супутник тощо).

5. Побудована модель вивчається всіма доступними методами, у тому числі – перевіркою з використанням різних підходів. На відміну від найпростіших випадків, які ми розглянули до цього часу, більшість моделей не піддаються чисто теоретичному аналізу, і тому необхідно широко застосовувати обчислювальні методи. Ця обставина особливо важлива при вивченні нелінійних об’єктів, оскільки їх якісна поведінка заздалегідь, як правило, невідома.

6. У результаті дослідження моделі не тільки досягається поставлена мета, але має бути встановлена усіма можливими способами (порівнянням з практикою, з іншими підходами) адекватність моделі – відповідність моделі до об’єкта та сформульованих припущень. Неадекватнамодель може дати результат, який буде як завгодно відрізнятися від істинного. Така модель має бути відкинутою або відповідним чином модифікованою.

3. ЗАСТОСУВАННЯ ТЕОРІЇ ПОДІБНОСТІ ПРИ ПОБУДОВІ МАТЕМАТИЧНИХ МОДЕЛЕЙ

Метою математичного моделювання є одержання адекватноїмоделі об’єкта, тобто моделі, яка однозначно відповідає об’єкту та припущенням щодо нього.

Одним з методів забезпечення адекватності є використання на етапі побудови математичної моделі теорії подібності. Сутність цієї теорії буде викладено для математичних моделей, основними визначальними рівняннями яких є диференціальні.

3.1. ЗНАХОДЖЕННЯ КРИТЕРІЇВ
ПОДІБНОСТІ ЯВИЩА ЗА НАЯВНОСТІ
ЙОГО МАТЕМАТИЧНОЇ МОДЕЛІ

Основні положення теорії подібності визначають властивості подібних об’єктів дослідження й указують вимоги, при задовольнянні яких один з об’єктів може розглядатися як модель (оригінал) відносно до інших.

Нагадаємо, що диференціальне рівняння є математичною моделлю класу процесів. Згідно з цим при інтегруванні будь-якого диференціального рівняння отримується нескінченна множина розв’язків, які задовольняють це рівняння. Щоб отримати з цієї множини можливих розв’язків один частинний, який відповідає певному конкретному процесу, необхідно мати додаткові дані, які не містяться у визначальному диференціальному рівнянні. Додаткові умови, які дозволяють із нескінченної множини розв’язків диференціального рівняння виділити один, який відповідає даному конкретному процесу, називаються умовамиоднозначності. Якщо конкретний процес відбувається і в часі, і в просторі, то умови однозначності включають просторові характеристики системи у початковий момент часу (початкові умови), а також умови на тій межі, де система контактує, взаємодіє з оточуючим середовищем (межові умови).

Перехід від класу явищ до одиничного явища відбувається приєднанням до диференціального рівняння умов однозначності. Таким чином, конкретний процес описується диференціальним рівнянням, розв’язки якого задовольняють певні умови однозначності.

Говорячи про подібність фізичних явищ при їх математичному моделюванні, ми повинні пам’ятати, що подібними називаються фізичні явища одного класу, у яких подібні всі характерні величини, тобто всі векторні величини геометрично подібні, а всі скалярні – відповідно пропорційні.

Наведемо кілька прикладів фізичної подібності.

1. Просторова (геометрична) подібність – виражається рівністю всіх відповідних кутів і пропорційністю всіх відповідних лінійних розмірів:

.

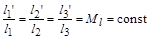2. Часова подібність (гомохронність) – виражається пропорційністю інтервалів між відповідними моментами часу:

.

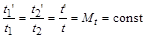Частинним випадком гомохронності є синхронність, за якої

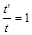, або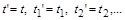

3. Кінематична подібність, тобто геометрична подібність полів швидкості (а також полів прискорення), виражається відповідністю напрямків і пропорційністю всіх швидкостей (прискорень):

.

4. Динамічна подібність, тобто геометрична подібність силових полів виражається відповідністю напрямків сил і їх пропорційністю:

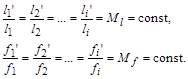
5. Температурна подібність, тобто геометрична подібність температурних полів, виражається відповідною пропорційністю всіх температур:

.

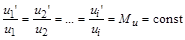Виходячи зі сказаного, подібність фізичних величин математично виражається у формі пропорцій таким чином:

1. Подібність скалярних величин (напр., температур):

.

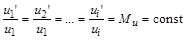2. Подібність векторних величин (напр., швидкостей) виражається відповідністю напрямків і пропорційністю їх абсолютних вартостей:

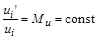
або пропорційністю координат відповідних векторів:

.

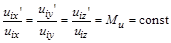У цих рівностях 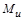– це сталий коефіцієнт пропорційності, так званий масштаб подібності (або стала подібності, множник подібного перетворення); позначення без верхнього індексу належать до першого фізичного явища або натури, індекс ´ – до другого фізичного явища або моделі; 1, 2, 3,..., належать і до відповідних точок простору (поля), і до відповідних моментів часу; індекси позначають компоненти векторної величини на відповідних координатних осях.

При моделюванні фізичних явищ масштаби подібностіємасштабами моделі: 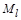є лінійним масштабом; 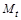– масштабом часу; 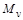–швидкості; 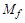–сил; 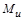– масштабом температур тощо.

Для подібності фізичних явищ необхідно й достатньо:

1. Незмінність (інваріантність) системи визначальних рівнянь математичної моделі при подібних перетвореннях змінних (заміні всіх змінних пропорційними їм величинами), тобто сумісність рівнянь

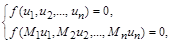
де 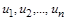– розмірні змінні; 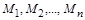– відповідні масштаби подібності.

2. Подібність усіх фізичних параметрів системи визначальних рівнянь математичної моделі.

3. Просторова (геометрична) подібність.

4. Стаціонарність фізичного явища (процесу) або подібність полів усіх змінних у початковий момент часу (тільки для нестаціонарних явищ).

5. Подібність межових умов, які входять до умов однозначності математичної моделі.

Розглянемо детальніше першу умову. У загальній теорії подібності доведено, що необхідною й достатньою умовою незмінності основних рівнянь математичної моделі відносно до подібного перетворення змінних величин є незмінність певних безрозмірних комплексів масштабів цих змінних. Переконаємося у справедливості цього твердження на прикладі.

Розглянемо подібне перетворення змінних рівняння теплопровідності. Нехай два процеси поширення тепла у твердих середовищах описуються диференціальними рівняннями

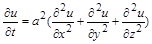, (1.3.1)

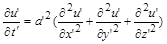. (1.3.2)

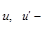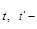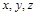У (1.3.1), (1.3.2) температура; час; і 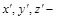просторові координати точок середовищ; 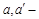коефіцієнти теплопровідності. Позначення без верхнього індексу належать до першого процесу (оригіналу), позначення з індексом ’ – до другого (моделі).

За припущенням процеси, що розглядаються, – подібні, тому між змінними, що характеризують процеси поширення тепла, і між фізичними параметрами 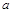і 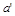, що характеризують властивості середовища, у якому поширюється тепло, існує такий зв’язок:

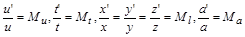
і, відповідно,

.

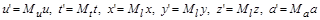Підставимо в рівняння (1.3.2) одержані значення змінних другого явища (моделі), тобто виконаємо подібне перетворення змінних у диференціальному рівнянні (1.3.2):

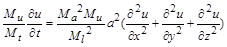. (1.3.3)

Ми очікуємо, що після виконаного подібного перетворення одержане рівняння (1.3.3) збіжиться з рівнянням (1.3.1), яке описує процес (оригінал). Для цього необхідно, щоб коефіцієнти рівняння (1.3.3), які є степеневими комплексами масштабів перетворення, були рівними між собою, тобто

.

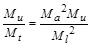Помножимо цю рівність на 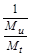, звідки матимемо ,

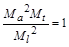або, якщо позначити

,

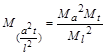то матимемо

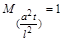. (1.3.4)

Таким чином, для інваріантності рівняння теплопровідності (1.3.1) до подібних перетворень необхідно, щоб масштаб подібності для безрозмірного комплексу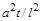

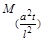
дорівнював одиниці. Це означає, що безрозмірний комплекс 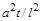має залишатися незмінним для подібних процесів теплопровідності. Дійсно, підставляючи у (1.3.4) замість масштабів подібності їх значення, матимемо

.

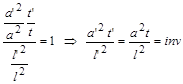Тут має місце незмінність(інваріантність – inv), а не сталість (const), оскільки одержані комплекси змінних однакові тільки для відповідних точок системи (полів), а для нестаціонарних процесів – і для відповідних моментів часу. Для різних точок системи й різних моментів часу одержані комплекси змінних можуть бути різними.

Безрозмірні комплекси, незмінність яких є кількісною ознакою подібності фізичних явищ, називаються критеріями подібності.

На конкретному прикладі ми переконались, що необхідною умовою незмінності визначальних рівнянь математичної моделі відносно до подібного перетворення змінних є незмінність критеріїв подібності. Нескладно також переконатись, що така умова є також і достатньою.

Отже, у тих випадках, коли математичні описання групи (двох або більше) якісно однакових процесів однієї й тієї ж фізичної природи є відомими і ці описання можуть бути перетвореними до однакового вигляду, тобто процеси, що розглядаються, є подібними, то такі процеси повинні мати однакові критерії подібності, які встановлюються безпосередньо з математичного описання шляхом приведення його до безрозмірного вигляду.

Таким чином, для знаходження критеріїв подібності фізичного явища за наявності диференціальних рівнянь, які служать його математичною моделлю, слід виконати такі дії:

1) необхідно вибрати одиниці виміру (масштаби) для всіх змінних величин, які входять у систему визначальних диференціальних рівнянь фізичного явища та умов їх однозначності;

2) усі змінні величини в рівняннях системи слід замінити їхніми безрозмірними значеннями, тобто їх відношеннями до вибраних масштабів;

3) степеневі комплекси з масштабів змінних величин і параметрів системи визначальних рівнянь, які при цьому утворюються, також приводяться до безрозмірного вигляду діленням усіх степеневих комплексів у рівнянні на один з них.

Безрозмірні степеневі комплекси, які при цьому отримуються, є шуканими критеріями подібності фізичного явища.

Розглянемо виконання вказаних дій при знаходженні критерію подібності явища поширення тепла в однорідному нерівномірно нагрітому твердому середовищі – явища, яке моделюється рівнянням теплопровідності

,

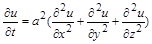де 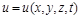– температура середовища; 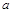– коефіцієнт температуропровідності; 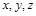– координати точок простору; – час.

За масштаби розмірних величин 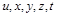вибираються деякі характерні величини, які на цьому першому етапі не обов’язково пов’язувати з конкретним явищем поширення тепла, яке моделюється. Позначимо відповідно 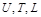масштаби температури 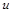, часу і координат 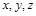. Ці масштаби використовуються для запровадження безрозмірних змінних :

.

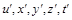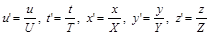Звідси розмірні змінні, які визначають явище теплопровідності, набувають вигляду

.
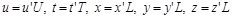