ВПЦ “Київський університет”, 2006 7 страница

в) за відсутності жертв хижаки вимирають за логістичним рівнянням

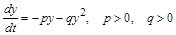, причому знак “–” перед 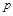вибирається на підставі припущення, що жертви є єдиним джерелом існування для хижаків;

г) наявність жертв викликає приріст, пропорційний як їх кількості, так і кількості хижаків (отже, права частина рівняння має містити доданок ).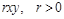

З вищенаведеного одержимо систему диференціальних рівнянь

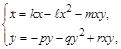(2.1.10)

що і є математичною моделлю еволюцій двовидової популяції.

Дослідимо дану модель.

Спочатку розглянемо випадок, коли конкуренцією всередині кожного виду можна знехтувати. Поклавши в системі (2.1.10) 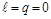, одержимо рівняння так званої моделі Лотки – Вольтерра:

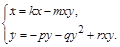(2.1.11)

Фазовим простором даної системи є перший квадрант. Розділивши перше рівняння на 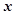, а друге – на 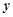, а потім проінтегрувавши їх, отримаємо систему інтегральних рівнянь вигляду

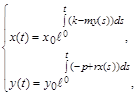(2.1.12)

з якої бачимо, що якщо 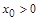і 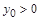, тобто розв’язок починався в першому квадранті, то він там весь час і знаходиться.

Еволюцію хижаків і жертв можна дослідити, не розв’язуючи систему (2.1.11), а намалювавши на площині 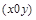її фазовий портрет. Знайдемо рівняння її фазових траєкторій. Розділивши перше рівняння на друге, отримаємо диференціальне рівняння траєкторій

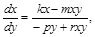
що має загальний інтеграл:

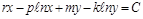. (2.1.13)

Система (2.1.11) має два положення рівноваги: точки 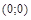і 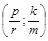. Щоб зобразити решту траєкторій, розглянемо функцію (рівняння поверхні)

.

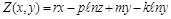Її лінії рівня і будуть шуканими кривими. Графік цієї функції має форму ями. У цьому неважко переконатися, пересікаючи поверхню паралельними осі OZ площинами, що проходять через точку . Сукупність зазначених площин описується рівнянням 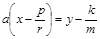, де 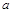– довільне. У перерізі даної поверхні з кожною з площин отримаємо криву, що описується рівнянням

.

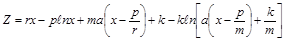При цьому

,

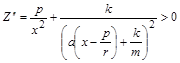а отже, усі криві опуклі вниз, що й доводить наше твердження.

Лінії рівня поверхні є замкнутими, тому й фазові криві системи Лотки
– Вольтерра є замкнутими кривими, що охоплюють положення рівноваги. Останнє означає, що розв’язки системи – періодичні функції часу.

Тепер зрозуміло, що в досліджуваній системі відбуваються незгасаючі коливання навколо положення рівноваги, тобто жодному виду вимирання не загрожує.

Проте, виникає питання: наскільки дана модель відповідає оригіналу? Адже система (2.1.11) не враховує всіх факторів, що можуть впливати на динаміку даної популяції. Зокрема, не бралась до уваги конкуренція між особинами одного виду 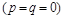. Тому більш точною є система вигляду (2.1.10). Лінеарізувавши її в околі положення рівноваги і знайшовши власні числа відповідної матриці лінійної системи, можна переконатися, що положення рівноваги – або асимптотично стійкий вузол, або асимптотично стійкий фокус. Мовою популяцій це означає, що з часом кількість особин кожного з видів прямує до рівноважного стану, і популяція не вимирає.

1.2.5. Модель багатовидової популяції

Наступною ланкою в ієрархічному ланцюзі є перехід до моделі багатовидової популяції. Розглянемо таку модель, а також укажемо на задачі, пов’язані з нею. Розв’язання таких задач може стати темою подальших наукових досліджень і кваліфікаційних робіт різного рівня.

Нехай 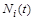– кількість особин і-го виду 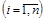. Математичною моделлю їх співіснування є узагальнення моделі Лотки – Вольтерра на 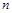рівнянь

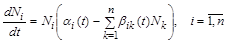, (2.1.14)

де 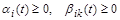– коефіцієнти системи.

Аналогічно можна переконатися, що перший квадрант є фазовим простором даної системи. При її дослідженні (навіть у випадку сталих коефіцієнтів) виникає низка серйозних математичних проблем, відповідь на які потрібно отримати в термінах коефіцієнтів системи, тобто функцій 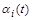і :

1. Дослідити умови конкурентного зникнення одного чи кількох видів, тобто умови, за яких 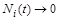при 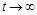для деяких .

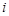2. Знайти умови обмеженості числа особин певного виду, тобто 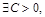щоб 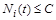для деяких .

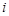3. Знайти умови періодичності зміни числа особин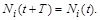

4. Дослідити умови перманентності системи (2.1.14).

Останнє означає існування в першому квадранті деякої компактної множини 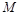, що має таку властивість: усі розв’язки системи (2.1.14), починаючи з деякого моменту часу (для кожного розв’язку – свого), лежать у даній множині.

З погляду біологічних популяцій, умови перманентності означають умови “мирного” співіснування всіх видів, коли жоден з видів не зникає.

1.2.6. Узагальнення моделі багатовидової популяції.
Побудова ієрархічного ланцюга

Узагальненням моделі (2.1.14) є модель, що враховує вплив зовнішніх факторів на розвиток популяції. Це може бути, наприклад, відловлення риби, збирання врожаю, запускання у водойму мальків. Проміжки часу, протягом яких відбувається зовнішній вплив, є малими порівняно з часом розвитку популяції, тому можна вважати, що такі впливи є миттєвими. Останнє приводить до математичних моделей, що є диференціальними рівняннями з імпульсною дією. Нехай 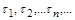– моменти зовнішніх впливів. Тоді, якщо , то популяції еволюціонує за законом, що описується системою (2.1.14), а в моменти 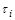відбувається стрибок розв’язку. У математичній формі це записується у вигляді

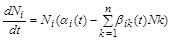
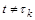
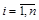, (2.1.15)

.

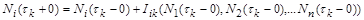Функції 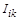характеризують величини зовнішніх впливів. Тобто розв’язками систем з імпульсною дією є кусково-розривні функції, на відміну від розв’язків звичайних диференціальних рівнянь, що значно ускладнює їх вивчення. Систематичне дослідження таких рівнянь було започатковано одночасно в Київському університеті імені Тараса Шевченка та Інституті математики НАН України й отримало подальший розвиток у роботах викладачів Київського університету.

Для імпульсних моделей можна ставити всі задачі, анонсовані в п. 1.2.5, а також порівнювати результати для ізольованих біологічних популяцій і популяцій, що зазнають впливу ззовні. Їх поведінка є зовсім різною. Наприклад, у популяції без зовнішнього впливу деякі види можуть зникати, а за рахунок зовнішньої корекції – відновлюватися. Усі проблеми, перелічені в п. 1.2.5, є досить цікавими й доволі складними математичними задачами для систем з імпульсами, розв’язання яких вимагає практика. На сьогодні ці проблеми розв’язані лише в деяких частинних випадках.

У всіх розглянутих вище моделях популяцій швидкість зміни їх чисельності залежить лише від їх кількості на даний момент. Однак швидкість залежить і від попередньої чисельності популяцій (особливо, якщо мова йде про людське суспільство, де суттєвим є людський фактор). Якщо врахувати таку залежність, то отримаємо математичну модель біологічної популяції, що є системою диференціальних рівнянь з післядією:

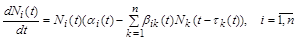, (2.1.16)

де функції характеризують запізнення. Порівняно з попередніми моделями, ця система є значно складнішим математичним об’єктом. Наприклад, множина розв’язків розглянутих вище рівнянь утворює скінченновимірний простір, розв’язки ж системи (2.1.16) – нескінченно вимірний. Теорія таких рівнянь знаходиться лише на початковій стадії розвитку. Для отримання більш-менш змістовних результатів у цьому напрямі потрібно залучати найсучасніші математичні методи. Однак мета виправдовує засоби. За допомогою даних рівнянь можна пояснити деякі ефекти, які не підлягають математичному дослідженню без урахування післядії. Наприклад, урахування часу 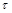– запізнення в логістичній моделі – приведе до рівняння

,

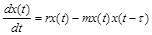де за певних співвідношень між 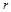та 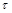удається встановити існування стійкого періодичного режиму коливань чисельності виду, на відміну від звичайної логістичної моделі. Такі коливання дійсно спостерігаються в деяких випадках і не можуть бути пояснені, виходячи з простої логістичної моделі.

Урахування запізнення в ланцюгу оберненого зв’язку математичної моделі локатора (відоме рівняння Мінорського) дозволило виявити стійкі коливання у 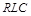-контурі на частоті, що дуже відрізняється від частоти контуру. Цей ефект було виявлено експериментально, але він не мав математичного пояснення, оскільки відповідні математичні моделі мали дуже малий степінь адекватності оригіналу. Введення запізнення в математичну модель процесу обробки деталі на токарному станку дозволило пояснити появу небажаних вібрацій різця. Ефект “галопування”, що спостерігався багатьма дослідниками під час руху літака ґрунтівкою, став очевидним, як тільки в лінійному рівнянні руху було враховане запізнення, викликане часом проходження літаком відстані між передніми й задніми колесами шасі. Урахування післядії бажано й у інших математичних моделях. Воно дозволить не тільки пояснити явища, експериментально виявлені раніше, але й передбачити нові ефекти. Якщо подібні роботи з’являються в інженерних журналах і монографіях порівняно рідко, то це, скоріше за все, викликано або складністю, або навіть повною відсутністю потрібного математичного апарату. Таким чином, моделі біологічних популяцій з урахуванням запізнення є наступною ланкою в побудові ієрархічного ланцюга.

Перейдемо до ще однієї ланки. Усі вказані вище моделі апріорі будувалися на тому, що кількість особин усіх видів у просторі розміщується однорідно. Якщо врахувати залежність кількості особин не тільки від часу, а й від розташування в просторі, то прийдемо до моделей біологічних популяцій з дифузією, що математично зображуються системою параболічних рівнянь у частинних похідних. Для одновидової популяції, де 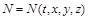– кількість особин у момент у точці 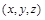, отримаємо рівняння

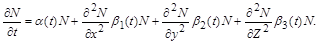
Таким рівнянням описується, наприклад, динаміка скупчення амеб. На сьогодні добре вивчена лише двовидова популяція з урахуванням дифузії.

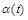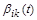Останньою, найвищою ланкою в ієрархічному ланцюзі є моделі, що враховують випадковий вплив на динаміку чисельності популяції. Усі впливи на популяцію носять випадковий характер і коефіцієнти і – випадкові процеси. У детермінованих моделях ці коефіцієнти є деякими усередненими характеристиками випадкових процесів.

Останнє означає, що детерміновані моделі дуже мало враховують випадковий характер впливу. Якщо його прийняти до уваги, то прийдемо до математичних моделей, що є диференціальними рівняннями з випадковими збуреннями. Аналіз таких рівнянь не менш складний, ніж рівнянь із запізненням. При їх дослідженні, окрім методів звичайних диференціальних рівнянь, використовуються методи теорії випадкових процесів. Отримані при цьому результати можуть якісно відрізнятися від аналогічних результатів детермінованого випадку. Так, наприклад, у логістичній моделі з урахуванням випадковостей можуть бути нестійкими обидва положення рівноваги або стійким нульове, а друге – нестійким, на відміну від звичайної логістичної моделі.

На завершення розгляду даних моделей наведемо схематично ієрархічний ланцюжок як приклад побудови ієрархій у математичному моделюванні (рис. 2.1.5).

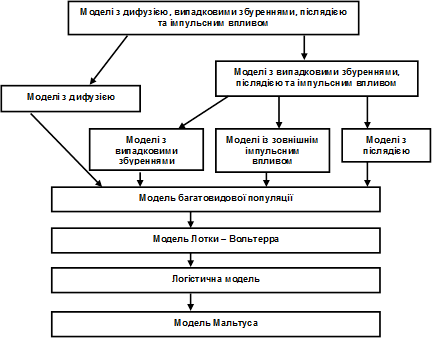
Рис. 2.1.5.

2. МОДЕЛІ ДЕЯКИХ ФІНАНСОВИХ
І СТРАХОВИХ ПРОЦЕСІВ

2.1. МАТЕМАТИЧНА МОДЕЛЬ РОБОТИ
СТРАХОВОЇ КОМПАНІЇ

Побудуємо й дослідимо математичну модель роботи страхової компанії. Вона організована таким чином. У початковий момент часу (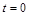) компанія має деякий початковий капітал 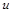. Клієнти компанії у проміжок часу 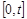роблять страхові внески згідно з договором. Позначимо їх сумарний капітал 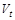. У цей же проміжок часу відбуваються страхові виплати клієнтам. Терміни й величини виплат є випадковими. Позначимо їх 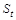. Тоді сумарний капітал 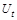страхової компанії в момент 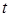дорівнюватиме

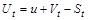. (2.2.1)

Задача страхової компанії полягає в організації роботи так, щоб компанія не зазнала банкрутства, тобто щоб для 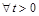. У зв’язку з цим виникає питання: яким має бути початковий капітал, щоб ? Оскільки 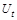залежить від випадкових чинників, то 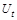у будь-який момент часу є випадковою величиною, а отже 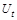– випадковий процес.

Позначимо через 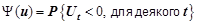і назвемо цю функцію ймовірністю банкрутства страхової компанії при стартовому капіталі 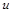. Відповідно функцію 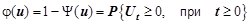назвемо ймовірністю небанкрутства. Дані функції відіграють ключову роль у роботі страхової компанії. Очевидно, що якщо ймовірність банкрутства досить велика, тобто 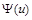близька до 1, то роботу компанії зі страховим капіталом 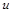розпочинати не варто.

Знайти аналітичний вигляд функцій 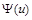і 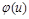у загальному випадку досить важко. Тому потрібно від реальної ситуації перейти до її математичної моделі, яка б, з одного боку, відповідала реальності, а з іншого – дозволяла б досліджувати функці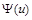ї і .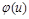

Розглянемо так звану класичну модель ризику. У цій моделі припускається, що страхові внески від клієнтів надходять за лінійним законом: 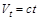( 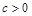– коефіцієнт інтенсивності внесків).

Розміри страхових виплат 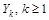– це випадкові величини, які вважаються незалежними, однаково розподіленими, з функцією розподілу мають математичне сподівання 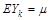і дисперсію .

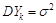Покладемо з імовірністю 1, тобто 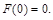Через 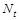позначимо кількість страхових виплат на 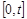. Очевидно, що 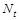– випадковий процес. Для нього зробимо припущення:

1) надходження вимог на виплату в інтервали часу, що не перетинаються – незалежні події;

2) розподіл кількості вимог на інтервалі 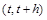залежить не від , а лише від 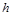(довжини інтервалу);

3) імовірність надходження хоча б однієї вимоги протягом часу 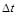дорівнює 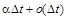, де – інтенсивність вимог, тобто ймовірність пропорційна довжині інтервалу;

4) імовірність надходження хоча б двох вимог на інтервалі 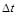дорівнює 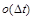, тобто вимоги виплати відбуваються не досить часто.

У теорії ймовірностей доводиться, що за виконання умов 1)-4) 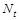є відомим процесом Пуассона, а тому для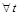 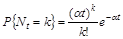, де 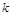– ціле додатне число. Отже, сума страхових виплат протягом часу 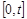дорівнює

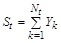. (2.2.2)

Тоді загальний прибуток компанії

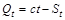. (2.2.3)

Означення. Випадковий процес 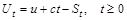називається процесом ризику.

Дослідимо отриману математичну модель.

У формулі (2.2.2) наведено суму випадкової кількості випадкових величин, що не залежать одна від одної та від 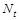. Відомо, що математичне сподівання 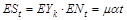(оскільки математичне сподівання процесу Пуассона дорівнює 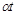). З моделі видно, що якщо 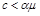, то страхова компанія з імовірністю 1 зазнає краху за будь-якого початкового капіталу.

Розглянемо 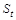у цілі моменти часу 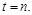Нехай 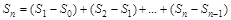– це послідовність сум незалежних, однаково розподілених випадкових величин зі скінченним математичним сподіванням. Із закону великих чисел (теорема Колмогорова) маємо, що 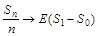при 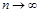з імовірністю 1. Однак 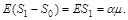Тому 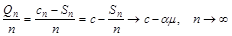з імовірністю 1. За умови 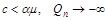і при довільному початковому капіталі через скінченний час 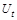стане менше нуля з імовірністю 1, тобто компанія зазнає краху. Отже, можна зробити висновок: роботу варто розпочинати, коли .

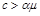Використовуючи формулу повної ймовірності для функції 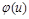, можна довести таку теорему.

Теорема. Функція 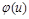є абсолютно неперервною й майже скрізь задовольняє інтегро-диференціальне рівняння

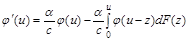. (2.2.4)

Рівняння (2.2.4) є складним і в загальному випадку не розв’язується, однак, коли страхові виплати мають показниковий розподіл з параметром ,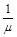

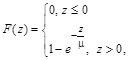(2.2.5)

то рівняння (2.2.4) розв’язується у явному вигляді.

Дійсно, у цьому випадку рівняння (2.2.4) має вигляд

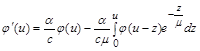. (2.2.6)

Диференціюючи його ще раз, отримаємо

.

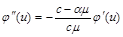Ввівши позначення 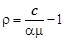( 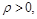оскільки 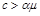), маємо

.

Це лінійне рівняння другого порядку. Його загальний розв’язок:

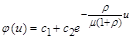. (2.2.7)

Із змісту функції 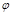маємо, що 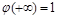(оскільки при нескінченному початковому капіталі банкрутство неможливе). Тому 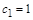. знайдемо зі значення 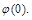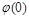можна знайти з таких міркувань.

Якщо рівняння (2.2.4) проінтегрувати на відрізку 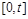, то можна отримати еквівалентне йому інтегральне рівняння

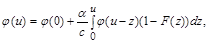(2.2.8)

перейшовши в якому до границі при 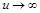і врахувавши, що 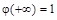, отримаємо, що 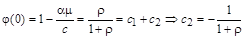. Таким чином, за умови

.

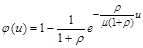Тоді ймовірність банкрутства

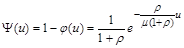. (2.2.9)

Подальший аналіз наведеної моделі пов’язаний з вивченням асимптотичної поведінки розв’язків рівняння (2.2.4) або (2.2.8) при 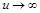і проводиться із застосуванням результатів, що були отримані при дослідженні випадкових процесів відновлення. Виявляється, що формула (2.2.9) є типовою для класичної моделі ризику, а сам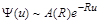е , де 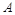– деяка функція від 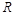, яку можна записати явно, а 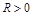– корінь деякого спеціального рівняння, який називається сталою Лундберга.

2.2. МОДЕЛЮВАННЯ РИНКУ ФІНАНСІВ

Використання фінансів, вкладання коштів завжди є дещо ризиковим – на прибуток чи збитки впливають різні випадкові чинники. Оцінити величину цього ризику, зменшити можливість збитків – задача фінансової математики, у якій широко застосовується теорія випадкових процесів.

Інвестор працює на ринку цінних паперів. Основними цінними паперами є облігації та акції.

Облігація – це позика на певний фіксований час, після якого повертаються гроші з фіксованим або плаваючим відсотком.

У найпростіших моделях фінансового ринку цей відсоток вважається детермінованим (невипадковим).

Позначимо B (t) – вартість облігації в час t, T – час погашення облігації, 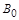– сума, що буде сплачена за договором, 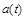– відсоткова ставка в момент t. Тоді буде виконуватись рівність на інтервалі [ t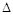, t+ t ]: