ВПЦ “Київський університет”, 2006 2 страница

2.2. МАТЕМАТИЧНІ МОДЕЛІ ТА ОСНОВНІ ЗАХОДИ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ

Основним поняттям методу математичного моделювання є поняття математичної моделі.

Математичною моделлю називається наближене описання якого-небудь явища або процесу оточуючого світу за допомогою математичної символіки.

На самому початку скористаємося тим, що при вивченні деяких розділів математики читач уже познайомився з деякими прийомами математичного моделювання. Так, вивченню рівнянь математичної фізики передує нехай невеликий, але системно дуже важливий, етап математичного моделювання. Саме на цьому етапі були виведені основні рівняння математичної фізики. Для цього використовується математичне моделювання поширення тепла в нерівномірно нагрітому середовищі, а також моделюються коливання закріпленої на кінцях струни. Моделювання цих процесів дозволило отримати основні рівняння математичної фізики: теплопровідності, хвильове рівняння, рівняння Лапласа й Пуассона, а також сформулювати для них крайові й змішані задачі. Отже, розпочнемо з того, що вже знаємо.

1. При математичному моделюванні вивчається не сам реальний фізичний процес, а деяка його модель, від якої вимагається, щоб вона зберігала основні риси процесу, що розглядається, і в той же час була настільки простою, щоб піддаватися вивченню математичними методами.

2. Створення математичної моделі фізичного явища можна розбити на такі етапи:

2.1. Вибирається основна величина (кілька основних величин), яка характеризує процес. При математичному моделюванні поширення тепла такою величиною є температура 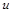точок середовища, яка в загальному випадку є функцією просторових координат 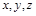і часу .

2.2. На другому етапі виводиться визначальне рівняння для основної величини, яка характеризує процес. При вивченні поширення тепла таким рівнянням є рівняння теплопровідності. Для виведення цього рівняння використовується закон збереження тепла в деякому довільному об’ємі нерівномірно нагрітого середовища.

2.3. Одержане на другому етапі диференціальне рівняння має безліч розв’язків. Отже, його не досить для описання конкретного процесу. Тому на третьому етапі побудови математичної моделі виводяться так звані умови однозначності, які з безлічі розв’язків визначального рівняння дозволяють виділити єдиний розв’язок, що характеризує даний процес, який моделюється. Нагадаємо, що для рівнянь математичної фізики такими додатковими умовами є крайові й початкові умови.

Таким чином, математична модель процесів, які вивчаються за допомогою рівнянь математичної фізики, складається з диференціального рівняння для основної величини, яка характеризує процес, і додаткових умов, які дозволяють отримати єдиний розв’язок цього рівняння – розв’язок, що описує даний, конкретний фізичний процес.

Після такого вступу перейдемо до основної частини розділу, у якому познайомимось з основними прийомами, що використовуються при виведенні визначальних рівнянь математичної моделі. Наприкінці розділу наведемо формалізовану схему математичного моделювання.

Основною тезою на початку буде така: другий етап побудови математичної моделі, тобто етап виведення визначального рівняння математичної моделі, є суттєво різним залежно від прийомів, які використовуються при її побудові. Розглянемо деякі підходи до побудови математичних моделей, які ілюструють застосування законів природи, варіаційних принципів, аналогій, ієрархічних ланцюгів. Це дає змогу обговорити такі поняття, як адекватність моделей, їх „оснащення”, нелінійність, чисельну реалізацію та низку інших фундаментальних понять математичного моделювання.

2.2.1. Використання законів природи

Найпоширеніший метод побудови математичних моделей полягає в застосуванні фундаментальних законів природи до конкретної ситуації. Ці закони загальновизнані, багаторазово підтверджені досвідом, служать основою великої кількості науково-технічних досягнень. Тому їх обґрунтованість не викликає сумніву, що, крім усього іншого, надає досліднику сильну психологічну підтримку.

Закон збереження енергії. Цей закон відомий майже двісті років і посідає, напевне, найбільш почесне місце серед великих законів природи. Покладаючись на нього, експерт з балістики, який хоче визначити швидкість револьверної кулі і не має поблизу спеціальної лабораторії, може скористатися відносно простим пристроєм типу маятника – вантажем, підвішеним на легкому недеформівному стрижні, який може вільно обертатися (рис. 1.2.1).

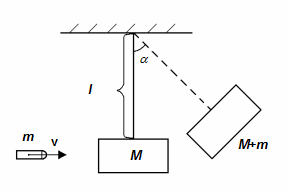
Рис. 1.2.1

Куля, яка застряє у вантажі, надає системі куля-вантаж свою кінетичну енергію, яка в момент найбільшого відхилення стрижня від вертикалі повністю переходить у потенціальну енергію системи. Ці трансформації описуються ланцюгом рівностей

.

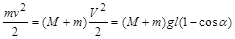Тут 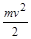– кінетична енергія кулі масою 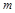, яка має швидкість 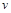; 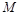– маса вантажу; 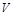– швидкість системи куля-вантаж відразу після зіткнення; 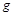– прискорення вільного падіння; 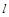– довжина стрижня; 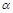– кут найбільшого відхилення. Шукана швидкість кулі 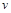, таким чином, визначається з формули

,

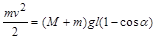а саме

,

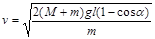яка є досить точною, якщо не враховані нами втрати енергії на нагрівання кулі й вантажу, на подолання опору повітря, розгін стрижня і т. д. є невеликими. Процеси, які відбуваються при зіткненні кулі й маятника, уже не є чисто механічними. Тому закон збереження механічної енергії, який був застосований у цьому підрозділі для обчислення величини 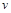, не є справедливим повною мірою: зберігається повна, а не механічна енергія системи. Закон збереження механічної енергії дає лише нижню межу для оцінки швидкості кулі.

Аналогічні міркування можна застосувати для оцінки часу свердління шару металу товщиною 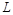лазером з потужністю 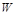, випромінювання якого є перпендикулярним до поверхні металу (рис. 1.2.2).

Рис. 1.2.2

Якщо енергія лазера повністю йде на випаровування стовпчика металу масою 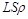, де 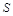– площа, яка опромінюється; 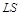– об’єм стовпчика; 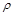– густина речовини, то закон збереження енергії виражається рівністю

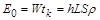, (1.2.1)

де 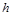– енергія, яка потрібна для випаровування одиниці маси. Величина 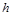має складну структуру: 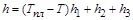, оскільки матеріал необхідно послідовно нагріти до температури плавлення 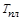, а потім розплавити й перетворити на пару; тут 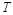– початкова температура; 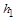– питома теплоємність; 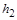і 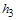– відповідно питома теплота плавлення й пароутворення.

Зміна глибини заглиблення 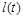із часом визначається з балансу енергії на проміжку часу від до 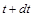. На випарувану за цей час масу

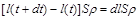
витрачається енергія 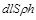, яка дорівнює енергії 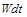, що надходить від лазера до речовини:

,

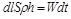звідки отримується диференціальне рівняння

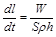. (1.2.2)

При інтегруванні цього рівняння слід використовувати умову, що початкова глибина заглиблення дорівнює нулю:

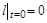. (1.2.3)

Інтегруючи (1.2.2) з урахуванням (1.2.3), матимемо

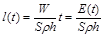, (1.2.4)

де 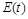– це вся енергія, яка була виділена лазером на момент часу . Отже, глибина заглиблення є пропорційною затраченій енергії. При 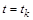, коли 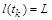, обчислення часу свердління шару металу товщиною 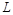дає однакові результати і з формули (1.2.1), і з формули (1.2.4):

.

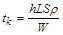Насправді процес свердління є набагато складнішим за розглянуту схему: енергія витрачається й на нагрівання речовини, і на виділення пари із заглиблення, яке може мати неправильну форму і т. і. Тому впевненість у правильності запропонованого математичного описання є значно меншою, ніж у випадку з кулею. Питання про відповідність об’єкта та його моделі – одне з центральних у математичному моделюванні.

Закон збереження матерії. Використання цього закону при створенні математичної моделі ілюструється таким прикладом. Нехай є невелика кількість радіоактивної речовини (урану), яка оточена товстим шаром звичайного матеріалу (напр., свинцю), – ситуація, яка є типовою при збереженні матеріалів, що розщеплюються, або при їх використанні в енергетиці (рис. 1.2.3).

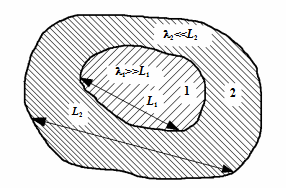
Рис. 1.2.3

Припущення про невелику кількість радіоактивної речовини є спрощувальним, воно дозволяє стверджувати, що всі продукти розщеплення без перешкод залишають область 1 без зіткнень з атомами речовини цієї області. Іншими словами, довжина вільного пробігу продуктів розщеплення 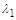у першій речовині значно більша за характерні розміри самого матеріалу 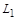, тобто 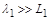. Слова „товстий шар” означають, що згідно з метою зберігання продукти розщеплення повністю поглинаються в області 2. Це гарантується при виконанні протилежної умови: 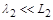, де 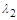– довжина вільного пробігу продуктів розщеплення у другій речовині; 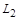– характерний розмір другої речовини.

Отже, усе, що вилітає з області 1, поглинається в області 2, і сумарна маса обох речовин з часом не змінюється. Це і є закон збереження матерії, застосований до даної ситуації. Якщо в початковий момент часу 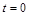маси речовин були рівними 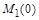і , то в будь-який момент часу є справедливим баланс

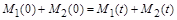. (1.2.5)

Одного рівняння (1.2.5), очевидно, недостатньо для знаходження поточних значень двох мас – 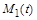і 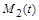. Для замикання математичного формулювання необхідно залучити додаткові дані про характер розщеплення. Ці дані формулюються таким твердженням: швидкість розщеплення (кількість атомів, які розпадаються в одиницю часу) є пропорційною загальній кількості атомів радіоактивної речовини.

За малий проміжок часу 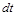між моментами і 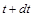усього розщепиться

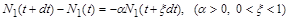(1.2.6)

атомів. Тут повторно використано закон збереження маси, але стосовно не всього процесу, а до відрізка часу 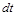. У цьому рівнянні, яке описує баланс атомів, у правій частині стоїть знак мінус (кількість речовини зменшується), а величина 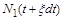відповідає деякому середньому значенню кількості атомів за час 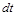. Перепишемо рівність (1.2.6) у диференціальній формі:

.

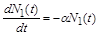Ураховуючи, що 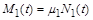, де 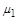– атомна вага речовини 1, отримаємо

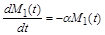. (1.2.7)

При самочинному (спонтанному) поділі ядер будь-який атом має деяку, не залежну від стану оточуючої речовини, імовірність розщеплення. Тому чим більша (менша) кількість самої радіоактивної речовини, тим більше (менше) виділяється продуктів розщеплення в одиницю часу. Коефіцієнт пропорційності (стала розщеплення) визначається конкретною речовиною. Рівняння (1.2.5) і (1.2.7) разом з умовами 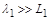і 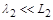, а також величинами 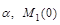і складають математичну модель об’єкта, який розглядається.

Інтегруючи (1.2.7), отримуємо, що маса матеріалу, який розщеплюється, зменшується за експоненціальним законом:

.

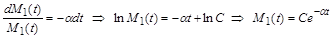При 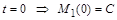, тому остаточно

.

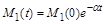При 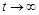в області 1 речовина повністю зникає.

Оскільки сумарна маса згідно з (1.2.5) залишається сталою, то в області 2 кількість речовини зростає:

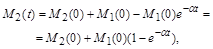
і при 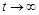продукти розщеплення повністю переходять з області 1 в область 2.

Закон збереження імпульсу. Човен, який стоїть нерухомо в безвітряну погоду на поверхні озера, почне рухатись уперед, якщо зробити кілька кроків від його носа до корми. Так виявляє себе закон збереження імпульсу, який стверджує: повний імпульс системи, на яку не діють зовнішні сили, зберігається. На переміщення весляра човен реагує зміщенням у протилежний бік.

Принцип реактивного руху покладено в основу багатьох технічних пристроїв, наприклад, ракети, яка виводить на орбіту Землі штучний супутник, для чого їй потрібно розвинути швидкість приблизно 8 км/с. Найпростіша математична модель руху ракети отримується із закону збереження імпульсу при нехтуванні опором повітря, гравітацією та іншими силами, за виключенням, звичайно, тяги реактивних двигунів.

Нехай продукти згоряння ракетного палива залишають розташовані в задній частині ракети вихлопні сопла зі швидкістю 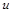(для сучасних палив швидкість 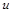дорівнює 3-4 км/с). За малий проміжок часу 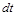між моментами і 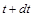частина палива вигоріла і маса ракети змінилася на величину 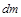. Змінився також імпульс ракети, але сумарний імпульс системи “ракета плюс продукти згоряння” залишився тим самим, що й у момент , тобто

,

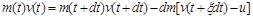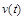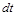де – швидкість ракети; – середня за проміжок швидкість витікання із сопел газів (обидві швидкості беруться відносно Землі). Перший член у правій частині цієї рівності – імпульс ракети в момент 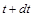, другий – імпульс, переданий газом, що витікає за час .

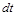Ураховуючи, що 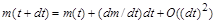, а також 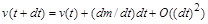, закон збереження імпульсу можна переписати у вигляді диференціального рівняння

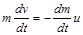, (1.2.8)

у якому член

,

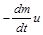очевидно, є ні чим іншим, як силою тяги ракетних двигунів. Рівняння (1.2.8) перетворимо до вигляду

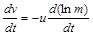(1.2.8а)

((1.2.8) )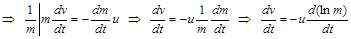

і проінтегруємо.

Після інтегрування рівняння (1.2.8а) матимемо

,

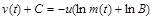де 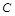і 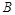– довільні сталі, або

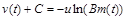. (1.2.8б)

Одержаний загальний розв’язок (1.2.8б) має задовольняти початкову умову: при 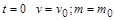, де 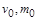– відповідно швидкість і маса ракети в момент часу .

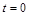Тому довільну сталу 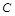слід узяти рівною 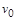, а довільну сталу 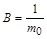. При цьому (1.2.8б) набуває вигляду

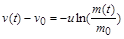
і при 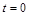перетворюється на тотожність. Звідси

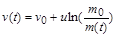. (1.2.9)

Якщо 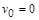, то максимальна швидкість ракети, яка досягається при повному згорянні палива, дорівнює

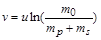. (1.2.10)

У (1.2.10) 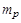– корисна маса (маса супутника); 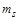– структурна маса власне ракетної конструкції – паливних баків, двигунів, систем управління тощо.

Формула (1.2.10) – це формула Ціолковського. Вона дозволяє зробити фундаментальний висновок про конструкцію ракети для космічних польотів. Уведемо величину 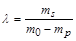, яка характеризує при 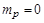відношення структурної й початкової мас ракети (без корисної маси, тобто супутника). Тоді для практично реальних значень 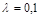і 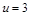км/с отримаємо при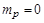

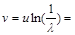7 км/с.

Звідси випливає, що навіть у самій ідеальній ситуації (корисна маса дорівнює нулю, відсутні гравітація та опір повітря тощо) ракета того типу, що розглядається, не здатна розвинути першої космічної швидкості. Звідси випливає важливий висновок – необхідно використовувати так звані багатоступеневі ракети.

Розглянутий приклад ілюструє також свого роду принцип найбільшого сприяння, який часто використовується на початковій стадії математичного моделювання складних об’єктів: якщо об’єкт, будучи поставленим у найкращі умови, не в змозі досягнути потрібних характеристик, то слід змінити сам підхід до об’єкта або пом’якшити вимоги до нього; якщо ж вимоги в принципі є досяжними, то наступні кроки пов’язані з дослідженням впливу на об’єкт додаткових, більш складних факторів.

2.2.2. Використання варіаційних принципів

Ще один підхід до побудови моделей полягає у використанні так званих варіаційних принципів. Цей підхід за широтою та універсальністю його можливостей можна зіставити з використанням фундаментальних законів природи при побудові математичних моделей. Варіаційні принципи є досить загальними твердженнями про об’єкт, що розглядається (система, явище), вони стверджують, що з усіх можливих варіантів поведінки об’єкта (руху, еволюції) вибираються лише ті, що задовольняють певну умову. Зазвичай згідно з цією умовою деяка величина, яка пов’язана з об’єктом, досягає свого екстремального значення при переході об’єкта з одного стану в інший.

Приклад. Припустимо, що автомобіль, який рухається зі сталою швидкістю 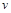, має потрапити з точки А в точку В і при цьому торкнутися деякої прямої лінії С. На рис. 1.2.4 показані різні траєкторії руху з точки А в точку В з дотиком до прямої С. Суцільною лінією виділено найкоротший шлях.

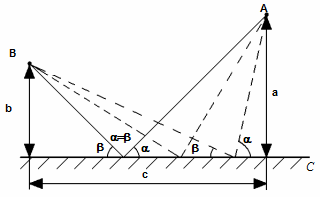
Рис. 1.2.4

Водій автомобіля дуже поспішає й вибирає з багатьох траєкторій шлях, який вимагає мінімальних затрат часу. Зобразимо витрачений час як функцію величини 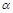– кута між прямою С і відрізком шляху від точки А до прямої С:

.

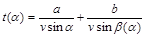Тут 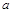і 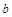– довжини перпендикулярів, які опущені з точок А і В на пряму С; 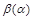– кут між прямою С і відрізком шляху з точки дотику до точки В.

Умова екстремальності 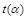за аргументом 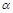означає, що

,

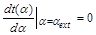або

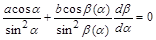. (1.2.11)

Для будь-яких значень 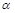є справедливою рівність

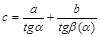, (1.2.12)

де 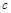– відстань між проекціями точок А і В на пряму С (ця відстань є однаковою для всіх траєкторій). Диференціюючи (1.2.12), отримаємо співвідношення

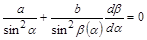, (1.2.13)

яке разом з умовою мінімальності (1.2.11) (порівняємо (1.2.11) і (1.2.13)) дає

,

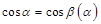тобто рівність кутів 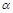і .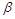

Далі неважко знайти самі значення 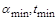через задані величини 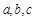. Однак зараз для нас важливо інше – умова мінімальності витрат часу привела до вибору відповідної траєкторії за правилом кут падіння дорівнює куту відбивання. Однак такому ж закону підкоряється і хід променя світла, який потрапляє на дзеркальну поверхню. Може, і промені світла рухаються траєкторіями, які забезпечують найшвидше потрапляння сигналу з однієї точки в іншу? Так, саме так і відбувається згідно з відомим варіаційним принципом Ферма, спираючись на який можна отримати всі основні закони геометричної оптики.

2.2.3. Застосування аналогій при побудові моделей

У дуже великій кількості випадків при побудові математичної моделі об’єкта абонеможливо прямо вказати фундаментальні закони чи варіаційні принципи, яким він підкоряється, або, з погляду наших сьогоднішніх знань, узагалі не можна бути впевненими в існуванні подібних законів, які допускають математичне формулювання. Одним із плідних підходівдо такого типу об’єктів є використання аналогій з уже вивченими явищами. Що, здавалося б, може бути спільного між радіоактивним розщепленням і динамікою популяцій, зокрема зі зміною чисельності населення нашої планети? Однак на найпростішому рівні така аналогія повністю спостерігається. Про це свідчить одна з найпростіших моделей популяцій, яка називається моделлю Мальтуса. В її основу покладено просте твердження: швидкість зміни населення з часом пропорційна її поточній кількості 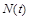, помноженій на різницю коефіцієнтів народжуваності 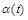і смертності 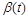. У результаті приходимо до рівняння