Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Правила оценки знаний в группе ДАТ -14 в 2014-15 уч. году по математике
|
|
Аттестация 1-го рубежного контроля
1 РК проводится после 7недель учебных занятий. Оценка будет складываться из результатов посещения занятий, наличия аккуратно оформленных конспектов лекций и практических занятий и выполнения контрольной работы на 6-7 неделе обучения.
При посещении всех лекционных и практических занятий студенту начисляется П1=100 баллов. За каждое пропущенное занятие из этого количества вычитается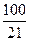 
=5 баллов. Итоговый балл за посещение П1 будет равен
П1= 100- 5 n, где n - количество пропущенных занятий.
При наличии аккуратно оформленных конспектов студенту также начисляется К1=100 баллов. Далее подсчёт идёт аналогично. При отсутствии конспектов,
К1= 100-5 n, где п - количество отсутствующих записей.
Результаты контрольной работы учитываются следующим образом:
Если в работе содержится N задач из которых m не решены, то оценка будет: S1= 100 – 
Итоговая оценка рубежного контроля Р1 является средней арифметической всех оценок.
Пример: К сроку рубежного контроля пропущено 6 занятий и не предоставлены конспекты 8 занятий, на контрольной работе из 10 задач не решены 3.
П1=100- 5*6=70; К1=100-5*8=60; S1=100-30=70
Р1 = 
баллов
«УТВЕРЖДАЮ»
Декан авиационного факультета
_________________Р.А. Искакова
«___» ______________2014г.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ПИСЬМЕННОМУЭКЗАМЕНУ по ВЫСШЕЙ МАТЕМАТИКЕ
(для специальности 5В071400 «Авиационная техника и технологии)
(1 семестр 2014-15 учебного года)
1.Прямоугольная и полярная системы координат на плоскости.
1. Общее уравнение прямой.
2. Уравнение прямой с угловым коэффициентом.
3. Уравнение прямой в отрезках на осях.
4. Условия параллельности и перпендикулярности прямых.
5. Угол между двумя прямыми.
6. Уравнение прямой, проходящие через две заданные точки.
7. Расстояние от точки до прямой.
8. Уравнение окружности.
9. Каноническое уравнение эллипса.
10. Каноническое уравнение гиперболы. Асимптоты гиперболы.
11. Уравнение параболы. Виды параболы.
12. Понятие вектора. Сложение векторов.
13. Умножение вектора на число. Вычитание векторов.
14. Разложение вектора по системе векторов.
15. Проекция вектора на ось.
16. Проекция вектора на оси 3-мерной системы координат. Разложение вектора по базису.
17. Скалярное произведение векторов и его свойства.
18. Условия параллельности и перпендикулярности векторов.
19. Уравнение плоскости в пространстве.
20. Уравнение плоскости в отрезках на осях.
21. Векторное произведение векторов и его свойства.
22. Условия параллельности и перпендикулярности плоскостей.
23. Каноническое уравнение прямой.
24. Параметрические уравнения прямой в пространстве.
25. Уравнение прямой в пространстве проходящей через две заданные точки.
26. Определители второго и третьего порядков.
27. Свойства определителей на примере определителя второго и третьего порядков.
28. Минор и алгебраическое дополнение элемента определителя. Разложение определителя по элементам какого-либо ряда.
29. Свойства определителя.
30. Решение неоднородной системы из трех уравнений с тремя неизвестными по формулам Крамера.
31. Метод Гаусса решения систем линейных уравнений.
32. Матрица. Типы матриц. Транспонированная матрица.
33. Равенство матриц. Сложение матриц. Умножение матрицы не число.
34. Минор и ранг матрицы.
Обратная матрица.
36.Произведение матриц и его свойства.
37. Переменные и их пределы. Величины бесконечно большие и бесконечно малые.
38. Теоремы о пределах последовательностей. Раскрытие некоторых типов неопределенностей.
39. Замечательные пределы.
40. Функции одной переменной. Классификации функций.
41. Предел функции в точке. Предел функции на бесконечности.
42. Односторонние пределы функции.
43. Бесконечно малые и бесконечно большие функции.
44. Сравнение функций. Эквивалентные бесконечно малые функции.
45. Классификация точек разрыва
46. Свойства непрерывных функций. Теорема Больцано-Коши
47.Прои з водная функция в точке, ее геометрический смысл.
48. Непрерывность функции, имеющей производную.
49. Производная суммы, разности, произведения и частного.
50. Правило дифференцирования сложной функции.
51. Теорема о производной обратной функции.
52. Логарифмическое дифференцирование.
53. Дифференциал функции и его геометрический смысл.
54. Условия монотонности функции.
55. Экстремум функции. Гладкая функция. Теорема Ферма.
(необходимое условие экстремума).
56. Достаточные условия экстремума.
57. Направление вогнутости графика функции (аналитический
признак).
58. Точки перегиба и выпрямления (необходимые условия,
Достаточные условия).
59. Теорема Ролля.
60. Теорема Лагранжа.
61. Теорема Коши.
62. Правило Лопиталя.
63. Теорема Тейлора.
64. Формы представления комплексных чисел.. Арифметические операции над комплексными числам
66. Возведение в степень и извлечение корня из комплексного числа.
67. Разложение дробно-рациональной функции на простейшие рациональные дроби.
68.Первообразная функции. Неопределенный интеграл и его свойства.
69.Методы интегрирования: замена переменной, интегрирование по частям.
70. Тригонометрические подстановки.
71. Интегрирование тригонометрических функций.
72. Определенный интеграл. Свойства. Приложения.
73. Несобственные интегралы
Составил: к.ф.м.н., доцент__________ Сапа А.В.
|
|