Квантовый гармонический осциллятор

Как известно, гармоническим осциллятором называется система, способная совершать гармонические колебания. В физике модель гармонического осциллятора играет важную роль, особенно при исследовании малых колебаний систем около положения устойчивого равновесия. Примером таких колебаний в квантовой механике являются колебания атомов в твердых телах, молекулах и т.д.

Рассмотрим одномерный гармонический осциллятор, совершающий колебания вдоль оси 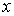под действием возвращающей квазиупругой силы 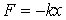. Потенциальная энергия такого осциллятора имеет вид

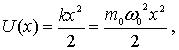
(4.77)

где 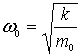- собственная частота классического гармонического осциллятора. Таким образом, квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы в параболической потенциальной яме (4.77).

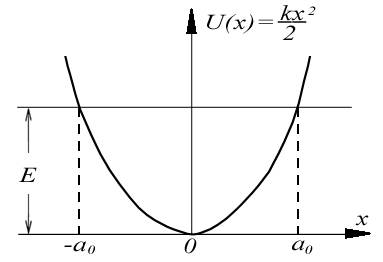
Рассмотрим сначала поведение классического гармонического осциллятора. Пусть частица с полной энергией 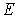совершает колебания в силовом поле (4.77) (рис.4.24). Точк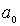и и 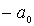, в которых полная энергия частицы равна потенциальной энергии 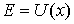, являются для частицы точками поворота. Частица совершает колебательные движения между стенками потенциальной ямы внутри отрезка 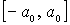, выйти за пределы которого она не может. Амплитуда колебаний 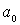определяется выражением .

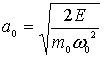Рис. 4.24.

В квантовой механике для решения задачи о гармоническом осцилляторе нужно решить уравнение Шредингера (4.6) с потенциальной энергией (4.77)

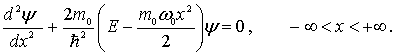
(4.78)

Вводя величины

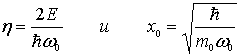
(4.79)

и переходя к новой безразмерной переменной 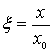, приводим уравнение (4.78) к виду

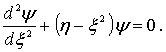
(4.80)

Анализ показывает, что волновые функции, являющиеся решением уравнения (4.80), будут непрерывными и конечными не при всех значениях параметра 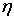, а лишь при

Выражая, согласно (4.79), энергию осциллятора 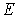через 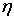, получаем

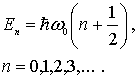
(4.81)

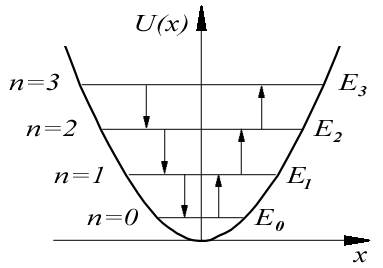
Это соотношение и определяет закон квантования энергии гармонического осциллятора. Отметим, что энергетические уровни гармонического осциллятора, в отличие, например, от случая прямоугольной потенциальной ямы, являются эквидистантными, т.е. расположены на одинаковом энергетическом расстоянии друг от друга (рис.4.25).

Рис. 4.25.

Еще одной важной особенностью спектра (4.81) является наличие так называемых нулевых колебаний - колебаний с энергией 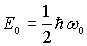, соответствующих значению квантового числа 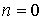. Отличие от нуля минимальной энергии осциллятора характерно, как мы уже видели, для всех квантовых систем и является следствием соотношения неопределенностей. В реальных квантовых системах, например, кристаллах, эти колебания сохраняются, как показывает опыт, даже при температурах, близких к абсолютному нулю, когда, казалось бы, все тепловое движение должно прекратиться.

Нулевые колебания играют в физике весьма важную роль, в частности они обусловливают отсутствие кристаллизации жидкого гелия при нормальном давлении даже при абсолютном нуле температур. Велика роль нулевых колебаний и в объяснении природы сил молекулярных взаимодействий, физических особенностей поверхностного натяжения, адсорбции и других молекулярных явлений. На эксперименте наличие нулевых колебаний наблюдается, в частности, в опытах по рассеянию света кристаллами при низких температурах.

Покажем, что значение нулевой энергии 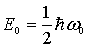есть как раз то минимальное значение энергии осциллятора, которое согласуется с требованиями соотношения неопределенностей. Поместим начало координат в точку, являющуюся положением равновесия гармонического осциллятора, совершающего колебания по закону 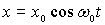. Тогда неопределенность координаты 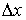принимает вид

Амплитуда колебаний 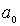связана с энергией 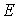соотношением 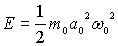, следовательно

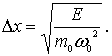
Аналогично, для неопределенности импульса имеем

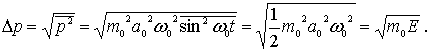
Подставляя 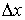и 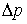в соотношение неопределенностей 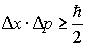, получаем следующее условие

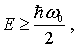
т.е. действительно, минимальное значение энергии гармонического осциллятора есть .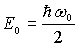

Эквидистантность энергетических уровней гармонического осциллятора (4.83) на первый взгляд означает, что осциллятор может поглощать и испускать излучение с частотой 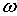, кратной 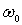, т.е. , где 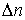- разность квантовых чисел начального и конечного уровней осциллятора. Однако, на самом деле это не так. Точный расчет, выходящий за рамки данного курса, показывает, что особенности испускания и поглощения электромагнитного излучения гармоническим осциллятором таковы, что возможны переходы только между соседними уровнями, т.е.

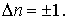
(4.82)

Условия, которые определяют изменение квантовых чисел при разрешенных переходах системы из одного состояния в другое, называются правилами отбора. Таким образом, правила отбора, характеризующие испускание и поглощение электромагнитного излучения гармоническим осциллятором, имеют вид (4.82).

Перейдем теперь к анализу волновых функций гармонического осциллятора. Как показано в теории дифференциальных уравнений с переменными коэффициентами, волновые функции, являющиеся решениями уравнения (4.80), имеют вид

(4.83)

где 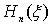- полином Чебышева-Эрмита 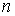-го порядка, определяемый выражением

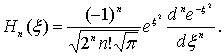
(4.84)

Отметим, что для этих полиномов справедливо рекуррентное соотношение

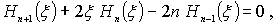
позволяющее найти 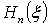для всех 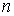, зная 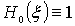и 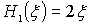. Например,

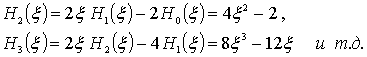
Волновые функции (4.83) ортонормированы, т.е. удовлетворяют условию

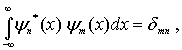
где - символ Кронекера (4.18).

Приведем вид волновых функций для первых трех энергетических уровней гармонического осциллятора

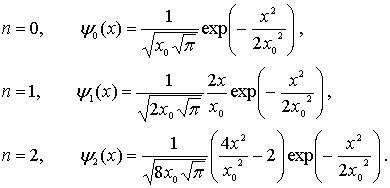
(4.85)

Графики волновых функций для значений квантового числа 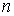от 0 до 5 представлены на рис.4.26. Отрезок 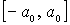определяет область, в

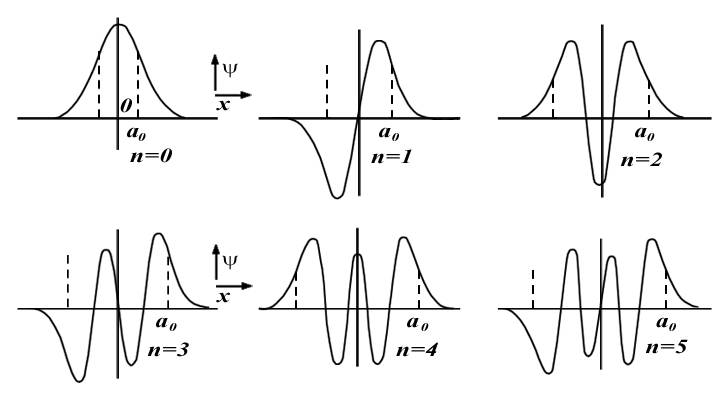
Рис. 4.26.

которой совершал бы колебания классический осциллятор. Ширина этой области оказывается различной для разных значений квантового числа 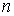, поскольку энергия осциллятора, а, следовательно, и амплитуда его колебаний также зависят от .

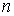Из (4.83) - (4.85) следует, что волновые функции гармонического осциллятора обладают определенной четностью. Они являются четными функциями координаты 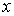при четных значениях 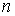и при 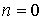, и нечетными функциями при нечетных 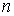. Значение квантового числа 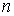определяет также число точек пересечения волновой функции с осью 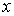. В основном состоянии, т.е. при 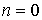, точки пересечения внутри параболической ямы отсутствуют, при имеется одна точка пересечения, при 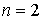- две и так далее. Таким образом, при увеличении квантового числа 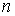на единицу волновая функция гармонического осциллятора меняет четность и приобретает добавочную точку пересечения с осью .

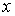Отметим, что вне классической области 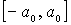волновые функции 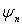отличны от нуля, что свидетельствует о том, что квантовый гармонический осциллятор с определенной вероятностью может находиться вне пределов параболической потенциальной ямы. В задаче 4.10 выполнен расчет вероятности пребывания частицы вне классической области для гармонического осциллятора, находящегося в основном состоянии.

При малых значениях квантового числа 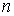плотность вероятности нахождения частицы, определяемая квадратом модуля волновой функции , кардинальным образом отличается от плотности вероятности обнаружения классического осциллятора

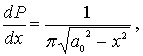
(4.86)

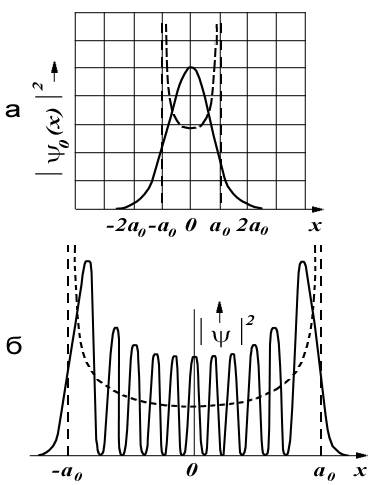
изображенной на рис.4.27 пунктирными линиями. Так, при 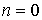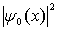имеет форму гауссовской кривой с

Рис. 4.27.

максимумом в точке 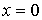, тогда как плотность вероятности обнаружения классического осциллятора (4.86) наоборот минимальна в точке 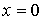и стремится к 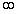в точках поворота, в которых скорость частицы обращается в нуль (рис.4.27а).

При значительной величине квантового числа 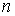, например, при 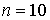функция приближается к классической кривой распределения. Она достигает максимума вблизи точек поворота и резко спадает вне классической области движения (рис.4.27б). При 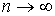кривая вероятности , как того и требует принцип соответствия, переходит в классическую функцию распределения плотности вероятности.

Отметим, что модель гармонического осциллятора и связанная с ним задача о движении частицы в параболической потенциальной яме является идеализацией, справедливой лишь при малых отклонениях колеблющейся частицы от положения равновесия. Во всех реальных ситуациях потенциальная энергия 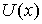частицы, совершающей колебания около положения равновесия, имеет более сложный по сравнению с (4.79) вид. Поэтому при возрастании амплитуды колебаний, начиная с некоторых значений амплитуд, движение частицы будет все больше отличаться от гармонических колебаний. Такое движение называют ангармоническим движением, а соответствующий осциллятор - ангармоническим осциллятором. Однако в случае малых колебаний влияние ангармонизма ничтожно мало, что позволяет использовать модель гармонического осциллятора для описания колебательного движения квантово-механических систем.

Выполненный в данной главе анализ движения частиц в прямоугольной и параболической потенциальных ямах показывает, что не смотря на отличие в форме ямы, в поведении частицы в яме имеется много общего:

1. Энергетический спектр частицы, находящейся в яме, является дискретным, т.е. энергия частицы квантуется.

2. Частица, находящаяся в основном состоянии, т.е. на самом низшем энергетическом уровне, обладает не равной нулю энергией.

3. Плотность вероятности нахождения частицы 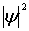имеет максимумы в области между классическими точками поворота и экспоненциально спадает вне классической области. Это означает, что с определенной вероятностью частица может находиться вне ямы (за исключением ям с бесконечно высокими, непроницаемыми, стенками).

4. При увеличении квантового числа 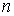на единицу волновая функция, описывающая поведение частицы в яме, приобретает дополнительную точку пересечения с осью .

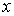Подчеркнем, что отмеченные свойства не зависят от формы потенциальной ямы, т.е. от вида потенциальной энергии .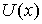

Следует отметить еще одно важное обстоятельство: энергетический спектр частицы является дискретным (энергия квантуется) только в тех случаях, когда частица находится в потенциальной яме. Если же частица движется в области потенциального порога, барьера, или над потенциальной ямой (при ), то ее энергетический спектр является непрерывным (квантование отсутствует). Этот результат согласуется с общей теоремой квантовой механики, согласно которой энергия всегда квантуется у систем, которые не могут уходить на бесконечность, и не квантуется у систем, способных уходить на бесконечность.