Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Постановки задачи линейного программирования
|
|
Общая постановка задачи линейного программирования (ОЗЛП)
Общая задача линейного программирования (ОЗЛП) может быть сформулирована следующим образом: найти значения переменных x1, x2, …, xn, максимизирующие линейную форму
(x1, x2, …, xn)= c1x1+…+cnxn (2.1)
при условиях
, i= 1, …, m1 (m1£ m) (2.2)
, i=m1+1, …, m (2.3)
xj ³ 0, j=1, …, p (p£ n) (2.4)
Соотношения (2.2) - (2.3) и (2.4) будем называть соответственно функциональными и прямыми ограничениями, выражение (2.1) - целевой функцией задачи линейного программирования (ЗЛП).
Значения переменных xj (j=1, 2, …, n) можно рассматривать как компоненты некоторого вектора 
=(x1, x2, …, xn) пространства Еn.
Определение 2.1. Планом или допустимым решением задачи линейного программирования будем называть вектор 
пространства Еn, компоненты которого удовлетворяют функциональным и прямым ограничениям задачи.
Множество всех планов задачи линейного программирования (2.1) – (2.4) будем обозначать Р.
Определение 2.2. План 
=(x1*, …xn*) будем называть решением задачи линейного программирования или ее оптимальным планом, если
или 
или 
Определение 2.3. Будем говорить, что задача линейного программирования разрешима, если она имеет хотя бы один оптимальный план.
Основная задача линейного программирования (ОснЗЛП)
ЗЛП во многих случаях оказывается ассоциированной с задачей распределительного типа или с задачей производственного планирования, в которой требуется распределить ограниченные ресурсы по нескольким видам производственной деятельности.
Такую ЗЛП можно поставить следующим образом: найти значения переменных x1, x2, …, xn, максимизирующие линейную форму
= 
(2.5)
при условиях
, i= 1, …, m (2.6)
xj ³ 0, j=1, …, n (2.7)
или в векторно-матричной форме
(2.8)
A 
£ 
(2.9)
³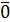 
, (2.10)
или 
, (2.11)
где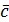 
= (с1, с2, …, сn); 
=(b1, b2, …, bm); А=(aij) – матрицы коэффициентов ограничений (2.6). Задача (2.5)- (2.7) или (2.8) – (2.10) называется основной ЗЛП. Основная ЗЛП является частным случаем общей ЗЛП при m1=m, p=n.
В линейном программировании широко используется аппарат линейной алгебры.
Каноническая задача линейного программирования (КЗЛП)
Для построения общего метода решения ЗЛП разные формы ЗЛП должны быть приведены к некоторой стандартной форме, называемой канонической задачей линейного программирования (КЗЛП).
В канонической форме
1. все функциональные ограничения записываются в виде равенств с неотрицательной правой частью;
2. все переменные неотрицательны;
3. целевая функция подлежит максимизации
Таким образом, КЗЛП имеет вид
(2.12)
, 
(2.13)
(2.14)
или в векторно-матричной форме
(2.15)
(2.16)
(2.17)
или
(2.18)
КЗЛП является частным случаем общей ЗЛП при m1=0, p=n
Любую ЗЛП можно привести к каноническому виду, используя следующие правила:
o минимизация целевой функции 
= c1x1+…+cnxn равносильна максимизации целевой функции - = -c1x1 -…-cnxn;
o ограничение в виде неравенства, например, 3x1+2x2-x3£ 6, может быть приведено к стандартной форме 3x1+2x2-x3+x4=6, где новая переменная x4 неотрицательна. Ограничение x1 - x2 + 3x3³ 10 может быть приведено к стандартной форме x1 - x2 + 3x3 - x5=10, где новая переменная x5 неотрицательна;
o если некоторая переменная x k может принимать любые значения, то ее можно представить в виде 
, где 
³ 0 и 
³ 0.
Для общей ЗЛП соответствующая каноническая форма имеет вид:
Для основной ЗЛП в векторно-матричной форме соответствующая КЗЛП имеет вид:
Пример 2.1.
Пусть ЗЛП имеет вид:
- не ограничена в знаке, 
Для приведения данной задачи к виду КЗЛП, выполним следующие шаги:
1. Представим свободную переменную 
в виде 
2. Введем дополнительные переменные 
(«избыточная» переменная) и 
(«остаточная» переменная) в первое и второе ограничения
3. Умножим первое ограничение на -1
4. Изменим знак 
на противоположный
В результате получим следующую КЗЛП, равносильную исходной
Теорема 2.1 (об эквивалентности КЗЛП и ОЗЛП).
Общая и соответствующая ей каноническая задачи линейного программирования эквивалентны в том смысле, что
1) если разрешима КЗЛП, то разрешима и ОЗЛП, и наоборот;
2) если множество планов КЗЛП пусто, то и множество планов ОЗЛП пусто, и наоборот;
3) если целевая функция КЗЛП не ограничена сверху на множестве планов КЗЛП, то и целевая функция ОЗЛП не ограничена сверху на множестве планов ОЗЛП, и наоборот.
Ключевую роль в теоретическом обосновании алгоритмов решения ЗЛП играют свойства множества P планов ЗЛП, в частности, свойства выпуклости и замкнутости.
|
|