Задача двох тіл. 1. Наведена маса. Задача про замкнуту систему двох точок називається задачею двох тіл

1. Наведена маса. Задача про замкнуту систему двох точок називається задачею двох тіл. Вона має просте і вичерпне розв‘язання - зводиться до основного завдання динаміки однієї матеріальної точки. Розв’язання задачі двох тіл використовується в небесній механіці, яка описує рух планет і їх супутників в Сонячній системі, в завданнях на зіткнення частинок, в статичній фізиці та інших питаннях. Розглянемо замкнуту систему двох матеріальних точок, які взємодіють між собою. Центр мас цієї системи рухається рівномірно і прямолінійно (або перебуває в стані спокою). Задача просто розвязується в системі з початком у центрі мас, що рухається поступально (така система називається Ц-системою). Позначимо маси частинок через і , їх радіус-вектори, проведені від центру мас, відповідно і 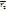(мал). Нехай - вектор, проведений від точки до . Із визначення радіус-вектора центру мас маємо: . Безпосередньо з малюнка випливає відношення між радіус-векторами: .

Два останніх рівності дозволяють виразити радіус-вектори через вектор , що з'єднує точки і . Маємо: . Напишемо тепер основні рівняння для руху обох точок в Ц-системі: Cили в системі рівнянь залежать від відстані між точками, а не від відстані до центру мас, тобто розв’язувати рівняння окремо для кожної точки можна. Однак саме в задачі двох тіл ці труднощі усуваються. Користуючись вищенаписаними виразами для радіус-векторів виключимо з основних рівнянь системи і 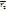. Отримуємо рівняння руху: . З огляду на те що за третім законом Ньютона = - , a, обидва рівняння стають тотожними, і рух системи двох точок в результаті їх взаємодії еквівалентно руху однієї точки відповідно до рівняння . Дане рівняння відрізняється від відомого рівняння руху матеріальної точки в полі заданої сили тільки тим, що замість маси тут виступає комбінація мас двох точок: . Величина називається наведеною масою. Отже, задача двох тіл звелася до задачі про рух однієї матеріальної точки з наведеною масою в Ц-системі під дією центральної сили; рівняння руху має звичайний вигляд: . Але при використанні результатів розв’язання отриманого рівняння необхідно пам'ятати, що точка , що рухається на кінці радіус-вектора під дією силового центру на початку координат Ц-системи, є не реальною, а зображує рух системи. Від її руху, після того як отримане рівняння проінтегруємо, слід переходити до реального руху двох матеріальних точок і .

2. Рух двох матеріальних точок у системі центру мас. Рух зображає точки відповідно до рівняння буде плоским, так як сила центральна. Нехай кінематі-
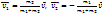тичне рівняння руху знайдено: . Знайдемо кінематичні рівняння руху обох матеріальних точок у Ц-системі: . Очевидно, що траєкторії руху зображає точки і точок і будуть подібними кривими відносно центру мас, а відношення подібності є зворотне відношення мас, тобто . Нескладно знайти і швидкість руху точок. Диференціюючи за часом, маємо: . Задача двох тіл розв’язана.

35. У питаннях динаміки важливу роль відіграють інертні властивості тіл. При поступальному русі інертні властивості тіла повністю визначаються масою тіла. Для обертального руху найістотніше значення має розподіл маси за обсягом твердого тіла. Інертні властивості твердого тіла в обертальному русі визначаються новою величиною - моментом інерції. Моментом інерції 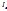тіла відносно осі s називають суму похідних окремих елементів dm маси тіла на квадрати їх відстаней до осі:

, де - об’ємна густина тіла.

За теоремою про середнє з інтегрального числення для моменту інерції можна написати після винесення з під знака інтеграла середнє значення підінтегральної функції наступний вираз:

Середнє значення квадратів відстаней елементів маси до даної осі називають квадратом плеча або радіусом інерції тіла.

Сума моментів інерції тіла відносно будь-яких трьох взаємноперпендикулярних прямих, що проходять через дану точку, є незмінною, яка не залежить від напряму прямих.

)dm=2H, де величина відносно початку координат і є сталою.

З наведених визначень випливає, що момент інерції залежить від вибору осі, по відношенню до якої він береться. Досліджуємо, як змінюється момент інерції тіла при зміні положення осі.

Зв'язок між моментами інерції відносно паралельних осей встановлюється за теоремою Штейнера: момент інерції тіла щодо даної осі дорівнює моменту інерції щодо паралельної осі, що проходить через центр мас тіла, доданої до добутку маси тіла на квадрат відстані між осями, що виражається рівністю

.

Для доведення об’єднаємо вісь Oz з віссю s, а вісь Ox направимо так, щоб вона перетинала паралельну вісь, що проходить через центр мас. Позначимо R і 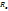-відстані від будь-якого елементу маси dm відповідно до осі s і осі, що проходить через центр мас. За визначенням маємо:

, .

З трикутника маємо:

Робимо підстановку у вираз і отримуємо:

За визначенням координат центру мас твердого тіла як неперервної системи точок dm маємо .

Теорему доведено.

Переходимо до вивчення залежності моменту інерції тіла відносно осі, що проходить через задану точку тіла, від напрямку осі. Розміщуємо в даній точці початок координат прямокутної декартової системи. Тоді положення осі визначається значеннями її трьох направляючих косинусів, які позначимо відповідно , і . Завдання поллягає в знаходженні моменту інерції як функція направляючих косинусів. Із трикутника ОАВ для квадрату відстані елемента маси dm від осі Os маємо наступний вираз: .

Виконуємо тотожні перетворення виразу для квадрату відстані :

.

Коефіцієнти при квадратах напрямних косинусів - моменти інерції тіла відносно координатних осей. Сталі величини ; ; мають однакову з моментами інерції розмірність.

Момент інерції є однорідною квадратичною функцією направляючих косинусів осі. Формула дозволяє визначити його відносно будь-якої осі, що проходить через задану точку, якщо відомі всі шість величин (i, k = 1, 2, 3). Ці величини відіграють важливу роль для своєрідних складових моменту інерції в даній системі координат. Звідси випливає, що, не будучи вектором, ця величина не є і скаляром. Вона належить до тензорних величин.

Головні осі інерції та головні моменти інерції для центру мас називаються відповідно головними центральними осями і моментами інерції тіла.

Тіло, у якого всі три головних центральних моменти інерції різні, називають асиметричною дзигою, якщо ж два моменти інерції однакові - симетричною дзигою, однакові три – кульовим.

Момент інерції тіла відносно будь-якої осі обчислюється за формулою і теоремою Штейнера.

36. Динаміка твердого тіла. Теорема про рух центру мас системи виражається за формулою m .(1)

Тепер сформулюємо її так: центр мас твердого тіла рухається як точка, в якій зосереджена маса всього тіла, а до неї додається головний вектор сил, що діють на тверде тіло.
Таким чином, у твердому тілі виділяється точка - центр мас, координати якої визначаються за формулами:

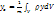, , , де густина тіла.

Центр мас рухається відповідно до рівняння (1). У проекціях на нерухомі осі координат Охуz маємо рівняння руху центру мас: Дані рівняння повністю розкривають задачу про рух твердого тіла у випадку поступального руху.

У загальному випадку просторова система сил, прикладених до твердого тіла, приводиться не до однієї рівнодіючої, а до рівнодіючої сили, яка дорівнює головному вектору системи , і до рівнодіючої пари, яка дорівнює головному моменту системи . Для визначення характеру руху твердого тіла і для розкладання його на поступальний і обертальний слід вибрати в якості точки прикладання рівнодіючої сили - центру приведення сил - центр мас тіла.

Після приведення сил система зводиться до рівнодійної сили і пари з моментом . Можливі такі окремі випадки:
= 0; тіло рухається поступально, якщо в початковий момент часу воно не мало обертання навколо осі, що проходить через центр мас. (Якщо тіло володіло в початковий момент часу кутовою швидкістю, то вона зберігається.)
= 0, 0; тіло обертається з кутовим прискоренням навколо миттєвої осі, що проходить через центр мас, а центр мас знаходиться у стані спокою або рухається зі сталою швидкістю.

0,, 0; центр мас рухається прискорено і тіло обертається з кутовим прискоренням навколо центру мас.

37. Умови рівноваги твердого тіла. Відповідно до того, що рух твердого тіла можна представити як сукупність поступального руху і обертання, умови його рівноваги зведуться до умов, що забезпечує рівність нулю прискорення центра мас і кутового прискорення. Тому, використовуючи формулу , отримуємо перше рівняння рівноваги: а з формули - друге рівняння рівноваги:

Таким чином, для рівноваги вільного тіла необхідно рівність нулю головного вектора і головного моменту сил, прикладених до нього.

Умови рівноваги для невільного тіла відповідно спрощуються. Так, для тіла з нерухомою віссю обертання - це рівність нулю суми моментів сил відносно осі, а з закріпленою точкою - щодо даної точки.

Приклад. Обертання твердого тіла навколо нерухомої осі.
У цьому простому випадку обертального руху твердого тіла застосування рівняння спрощується. По-перше, положення рухомої осі, що збігається з напрямком Ь (наприклад, О'z '), з плином часу не змінюється, тому маємо тільки

де при диференціюванні береться похідна від відповідної проекції.
По-друге, в даному випадку 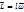, якщо момент інерції тіла відносно зазначеної осі обертання.
Таким чином, маємо рівняння руху для тіла: за формою аналогічне основному рівнянню динаміки матеріальної точки. У цьому випадку рух вичерпується одним скалярним рівнянням (в проекціях на вісь обертання): = М, з якого, зокрема, випливає, що постійний момент викликає рівноприскорене обертання. Можна також розглядати приклади: фізичного маятника, руху вільної симетричної дзиги, руху симетричної дзиги під дією сил, гіроскоп і гіроскопічний момент.

38. Кінетична енергія твердого тіла
Формула кінетичної енергії твердого тіла. Знайдемо формулу кінетичної енергії твердого тіла. Будемо виходити з теореми Кеніга для системи матеріальних точок:
Перший член представляє тут кінетичну енергію поступального руху системи зі швидкістю центру мас. Якщо застосувати формулу до твердого тіла, він не змінюється. Другий член в представляє суму кінетичної енергії всіх точок при їх рухах щодо центру мас (центру інерції) зі швидкостями . Для твердого тіла це будуть швидкості його елементів dm, рух яких обмежено умовою сталості форми і розмірів тіла. Рух елементів твердого тіла відносно системи, що рухається поступально разом з центром мас, має місце тільки внаслідок обертання тіла навколо миттєвої осі, проходячий через центр мас.

Швидкість руху точки твердого тіла відносно центру мас , де - радіус-вектор, проведений до елементу маси dm з центру мас С. Кінетична енергія обертального руху твердого тіла навколо осі s ( - одиничний вектор осі), що проходить через центр мас тіла, виразиться таким інтегралом, поширеним за об’ємом тіла: dm. Помітивши, що rsin () = , отримаємо:

Але величина інтеграла є моментом інерції ції тіла відносно осі.

Отже, кінетична енергія обертання твердого тіла визначається формулою

а повна кінетична енергія твердого тіла виражається тепер наступною рівністю:

де перший член описує кінетичну енергію тіла при поступальному русі, другий - при обертальному. Обидва члени є незалежними в тому відношенні, що не пов'язані один з одним через швидкості, тому можуть застосовуватися окремо.

Але отримана формула для кінетичної енергії обертального руху твердого тіла

може бути використана для обчислення тільки у випадку, коли вектор кутової швидкості не змінює свого напрямку при русі тіла (наприклад, при обертанні тіла навколо нерухомої осі). Якщо ця умова не виконується, момент інерції , стає змінною величиною і формула практично виявляється непридатною для використання. У цьому випадку виражаємо момент інерції , щодо миттєвої осі обертання через головні моменти інерції за формулою Тоді для кінетичної енергії обертального руху отримуємо такий вираз: .Запишемо вираз кінетичної енергії обертання твердого тіла через проекції моменту імпульсу на головні вісі інерції:

Для тіла з нерухомою віссю обертання ця формула спрощується:

На поступальному переміщенні твердого тіла «працює» головний вектор системи сил, а на обертальному - головний момент.

Теорема про зміну кінетичної енергії твердого тіла запишеться наступною рівністю:

37. Умови рівноваги твердого тіла. Відповідно до того, що рух твердого тіла можна представити як сукупність поступального руху і обертання, умови його рівноваги зведуться до умов, що забезпечує рівність нулю прискорення центра мас і кутового прискорення. Тому, використовуючи формулу , отримуємо перше рівняння рівноваги: а з формули - друге рівняння рівноваги: Таким чином, для рівноваги вільного тіла необхідно рівність нулю головного вектора і головного моменту сил, прикладених до нього. Умови рівноваги для невільного тіла відповідно спрощуються. Так, для тіла з нерухомою віссю обертання - це рівність нулю суми моментів сил відносно осі, а з закріпленою точкою - щодо даної точки.

Приклад. Обертання твердого тіла навколо нерухомої осі.
У цьому простому випадку обертального руху твердого тіла застосування рівняння спрощується. По-перше, положення рухомої осі, що збігається з напрямком Ь (наприклад, О'z '), з плином часу не змінюється, тому маємо тільки

де при диференціюванні береться похідна від відповідної проекції.
По-друге, в даному випадку 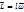, якщо момент інерції тіла відносно зазначеної осі обертання.

Таким чином, маємо рівняння руху для тіла: за формою аналогічне основному рівнянню динаміки матеріальної точки. У цьому випадку рух вичерпується одним скалярним рівнянням (в проекціях на вісь обертання): = М, з якого, зокрема, випливає, що постійний момент викликає рівноприскорене обертання. Можна також розглядати приклади: фізичного маятника, руху вільної симетричної дзиги, руху симетричної дзиги під дією сил, гіроскоп і гіроскопічний момент.

38. Кінетична енергія твердого тіла
Формула кінетичної енергії твердого тіла. Знайдемо формулу кінетичної енергії твердого тіла. Будемо виходити з теореми Кеніга для системи матеріальних точок:
Перший член представляє тут кінетичну енергію поступального руху системи зі швидкістю центру мас. Якщо застосувати формулу до твердого тіла, він не змінюється. Другий член в представляє суму кінетичної енергії всіх точок при їх рухах щодо центру мас (центру інерції) зі швидкостями . Для твердого тіла це будуть швидкості його елементів dm, рух яких обмежено умовою сталості форми і розмірів тіла. Рух елементів твердого тіла відносно системи, що рухається поступально разом з центром мас, має місце тільки внаслідок обертання тіла навколо миттєвої осі, проходячий через центр мас.

Швидкість руху точки твердого тіла відносно центру мас , де - радіус-вектор, проведений до елементу маси dm з центру мас С. Кінетична енергія обертального руху твердого тіла навколо осі s ( - одиничний вектор осі), що проходить через центр мас тіла, виразиться таким інтегралом, поширеним за об’ємом тіла: dm. Помітивши, що rsin () = , отримаємо:

Але величина інтеграла є моментом інерції ції тіла відносно осі.
Отже, кінетична енергія обертання твердого тіла визначається формулою
а повна кінетична енергія твердого тіла виражається тепер наступною рівністю:
де перший член описує кінетичну енергію тіла при поступальному русі, другий - при обертальному. Обидва члени є незалежними в тому відношенні, що не пов'язані один з одним через швидкості, тому можуть застосовуватися окремо.
Але отримана формула для кінетичної енергії обертального руху твердого тіла

може бути використана для обчислення тільки у випадку, коли вектор кутової швидкості не змінює свого напрямку при русі тіла (наприклад, при обертанні тіла навколо нерухомої осі). Якщо ця умова не виконується, момент інерції , стає змінною величиною і формула практично виявляється непридатною для використання. У цьому випадку виражаємо момент інерції , щодо миттєвої осі обертання через головні моменти інерції за формулою Тоді для кінетичної енергії обертального руху отримуємо такий вираз: .Запишемо вираз кінетичної енергії обертання твердого тіла через проекції моменту імпульсу на головні вісі інерції:

Для тіла з нерухомою віссю обертання ця формула спрощується:

На поступальному переміщенні твердого тіла «працює» головний вектор системи сил, а на обертальному - головний момент.
Теорема про зміну кінетичної енергії твердого тіла запишеться наступною рівністю: