
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Два способа оценки погрешности при косвенных измерениях.
|
|
В случае косвенных измерений физических величин возможны два способа вычисления окончательного результата и погрешности.
Первый способ.
Для каждой измеряемой физической величины проводят серию измерений. Эти измерения (прямые) обрабатывают и находят средние значения 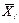 и соответствующие им доверительные интервалы
и соответствующие им доверительные интервалы 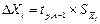 с одной и той же доверительной вероятностью. Затем по выражению функциональной зависимости Y = f (X 1, X 2, … X n) находят среднее значение искомой физической величины, используя найденные средние значения всех измеренных величин
с одной и той же доверительной вероятностью. Затем по выражению функциональной зависимости Y = f (X 1, X 2, … X n) находят среднее значение искомой физической величины, используя найденные средние значения всех измеренных величин 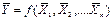 . Затем по формулам переноса ошибок (формула 19 или ее частные случаи) рассчитывают доверительный интервал величины Y.
. Затем по формулам переноса ошибок (формула 19 или ее частные случаи) рассчитывают доверительный интервал величины Y.
Пример
Задача - определить ускорение свободного падения с помощью математического маятника.
Формула для расчета - 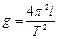 , где l - длина маятника, T - период его колебаний.
, где l - длина маятника, T - период его колебаний.
Измерили 5 раз длину маятника и 5 раз его период. Получили следующие значения, которые обработали, как прямые измерения:
Таблица 3
| l(м) |  (м) (м)
| 
| 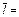 0, 9644 0, 9644
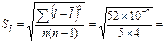 = 0, 00051
D = 0, 00051
D 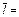 3, 2´ 0, 00051=0, 0016 3, 2´ 0, 00051=0, 0016
| |||
| 0, 965 | 0, 0006 | 3, 6 ´ 10-7 | ||||
| 0, 966 | 0, 0016 | 25, 6´ 10-7 | ||||
| 0, 964 | -0, 0004 | 1, 6´ 10-7 | ||||
| 0, 963 | -0, 0014 | 19, 6´ 10-7 | ||||
| 0, 964 | -0, 0004 | 1, 6´ 10-7 | ||||
| S | 4, 822 | 52´ 10-7 | ||||
| Т (сек) | Т- 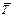
| (Т-  )2 )2
| 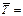 1, 9698 1, 9698
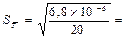 =0, 000583
D
=0, 000583
D 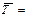 3, 2´ 0, 000583 =0, 001866»0, 0019 3, 2´ 0, 000583 =0, 001866»0, 0019
| |||
| 1, 970 | 0, 0002 | 0, 04´ 10-6 | ||||
| 1, 969 | -0, 0008 | 0, 64´ 10-6 | ||||
| 1, 971 | 0, 0012 | 1, 44´ 10-6 | ||||
| 1, 968 | -0, 0018 | 3, 24´ 10-6 | ||||
| 1, 971 | 0, 0012 | 1, 44´ 10-6 | ||||
| S | 9, 849 | 6, 8´ 10-6 | ||||
Получили: 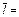 0, 9644 и
0, 9644 и 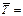 1, 9698.
1, 9698.
Затем рассчитывают 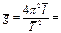
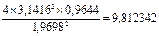
и, в соответствии с формулой (7) рассчитывают относительную погрешность g:

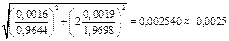 .
.
Тогда D g = g ´ d g = 9, 812342 ´ 0, 0025=0, 0249» 0, 025, и окончательный результат, соответственно: 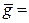 (9, 812±0, 025) м/с2 при Р=0, 95
(9, 812±0, 025) м/с2 при Р=0, 95
Второй способ.
В случаях, когда по условиям опыта измерения делаются в не воспроизводимых условиях, значения функции, Y = f (X 1, X 2, … X n) вычисляют для каждой отдельной серии измерений { X i}, а затем полученный ряд значений Yi, обрабатывают по алгоритму прямых измерений.
Пример
Пусть поставлена та же задача - определить g, но при этом имеется несколько (пять) заведомо различных маятников. В этом случае рационально поступить следующим образом. Для каждого маятника измерить его длину и период колебаний. По этим значениям рассчитать величину g (для каждого маятника независимо). Полученные значения g обработать, как прямые измерения.
Таблица 4
| № маятника | L( м ) | Т (сек) | g (м/с2) | 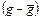
| 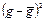
|
| 0, 965 | 1, 970 | 9, 816453 | 0, 00355 | 0, 126032´ 10-4 | |
| 1, 222 | 2, 222 | 9, 771086 | -0, 041817 | 17, 48669´ 10-4 | |
| 1, 568 | 2, 510 | 9, 825584 | 0, 01268 | 1, 60795´ 10-4 | |
| 0, 559 | 1, 498 | 9, 834401 | 0, 0215 | 4, 62167´ 10-4 | |
| 0, 752 | 1, 739 | 9, 816991 | 0, 00409 | 0, 167152´ 10-4 | |
| S | 49, 06452 | 24, 0095´ 10-4 |
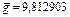
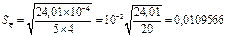 ,
,
D g = 3, 2´ 0, 01096 =0, 035
и, соответственно, окончательный результат:
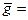 (9, 813±0, 035) м/с2 при Р=0, 95
(9, 813±0, 035) м/с2 при Р=0, 95
|
|