
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Частные производные сложной функции
|
|
Пусть в области  задана функция двух переменных:
задана функция двух переменных:
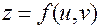 , (6)
, (6)
у которой переменные 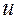 и
и  в свою очередь являются функциями переменных
в свою очередь являются функциями переменных 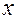 и
и 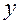 :
:
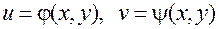 , (7)
, (7)
заданными в области 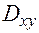 .
.
Тогда 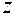 является сложной функцией независимых переменных
является сложной функцией независимых переменных 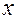 и
и 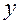 с промежуточными переменными
с промежуточными переменными 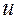 и
и  :
:
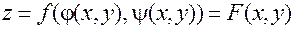 . (8)
. (8)
Рассмотрим задачу нахождения частных производных 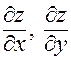 этой сложной функции без использования явной записи (8).
этой сложной функции без использования явной записи (8).
Пусть точка 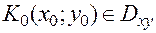 , и функции
, и функции 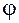 и
и 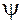 , согласно уравнениям (7), переводят ее в точку
, согласно уравнениям (7), переводят ее в точку 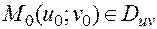 :
:
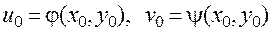 .
.
Теорема. Пусть выполняются три условия:
1. В окрестности точки 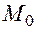 существуют частные производные
существуют частные производные 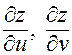 , непрерывные в самой точке
, непрерывные в самой точке 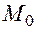 .
.
2. В точке 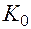 существуют частные производные
существуют частные производные 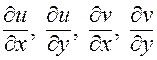 .
.
3. Функции 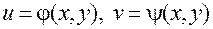 непрерывны в точке
непрерывны в точке 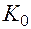 .
.
Тогда в точке 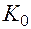 существуют частные производные сложной функции
существуют частные производные сложной функции 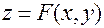 , и для них справедливы формулы:
, и для них справедливы формулы:
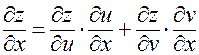
(9)
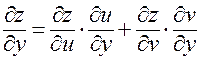 ,
,
или в другой записи:
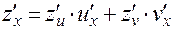
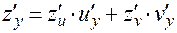 .
.
Доказательство. Проведем его для частной производной 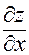 . Придадим переменной
. Придадим переменной 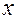 в точке
в точке 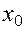 приращение
приращение 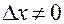 ; оно вызовет частные приращения
; оно вызовет частные приращения 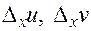 промежуточных переменных
промежуточных переменных 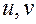 , которые в свою очередь вызовут частное приращение
, которые в свою очередь вызовут частное приращение 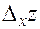 сложной функции
сложной функции 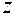 . В силу непрерывности частных производных (условие 1) к приращению
. В силу непрерывности частных производных (условие 1) к приращению 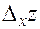 применима формула (4):
применима формула (4):
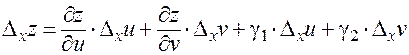 ,
,
откуда, деля на 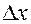 , получаем:
, получаем:
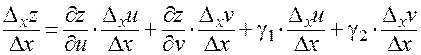 . (10)
. (10)
Здесь 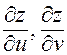 — постоянные величины для фиксированной точки
— постоянные величины для фиксированной точки 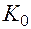 . Далее, в силу непрерывности функций
. Далее, в силу непрерывности функций 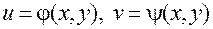 (условие 3):
(условие 3):
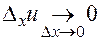 ,
, 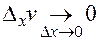 ,
,
а тогда и величины 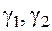 в представлении (10) также стремятся к нулю.
в представлении (10) также стремятся к нулю.
Переходя в равенстве (10) к пределу при 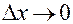 , получаем на основании свойств предела и условия 2:
, получаем на основании свойств предела и условия 2:
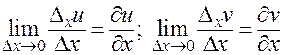 ,
,
и далее,
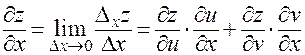 .
.
Замечание. Аналогичные формулы имеют место для функций большего числа переменных. Например, в ситуации:
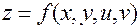 ,
,
и
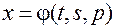 ,
, 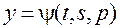 ,
, 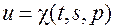 ,
, 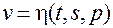 ,
,
имеем:
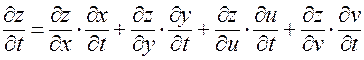
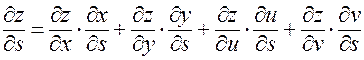
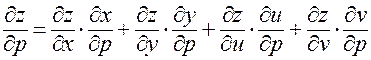
Пример. Пусть
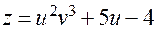 ;
;
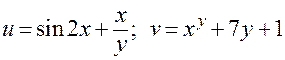 .
.
Тогда
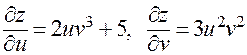 ;
;
далее,
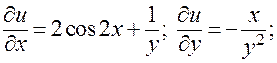
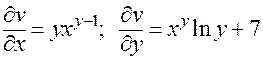
Поэтому
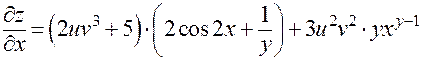 ;
;
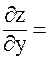
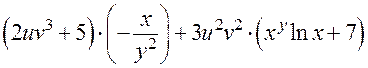 .
.
|
|
